Menu Close

solve-inside-C-x-1-x-3-x-1-x-2-x-1-x-1-0-

Tinku Tara 0 Comments
Pin




Question Number 96211 by mathmax by abdo last updated on 30/May/20
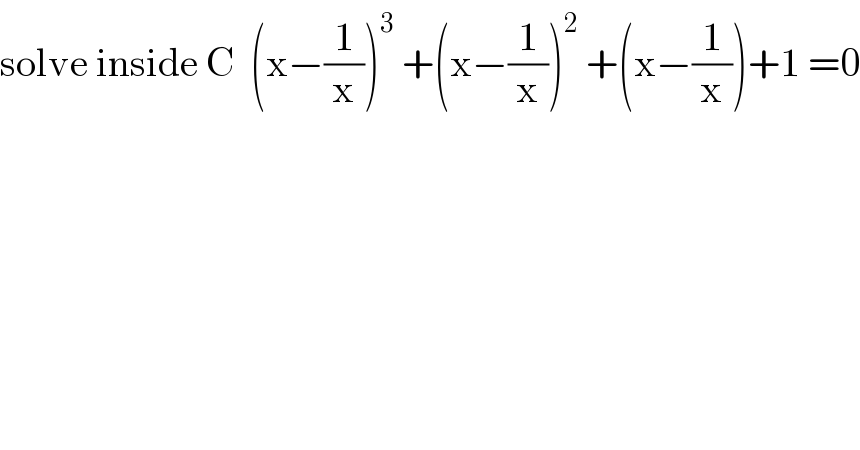
solve inside C (x−(1/x))^3 +(x−(1/x))^2 +(x−(1/x))+1 =0
solveinsideC(x−1x)3+(x−1x)2+(x−1x)+1=0
Answered by mr W last updated on 30/May/20
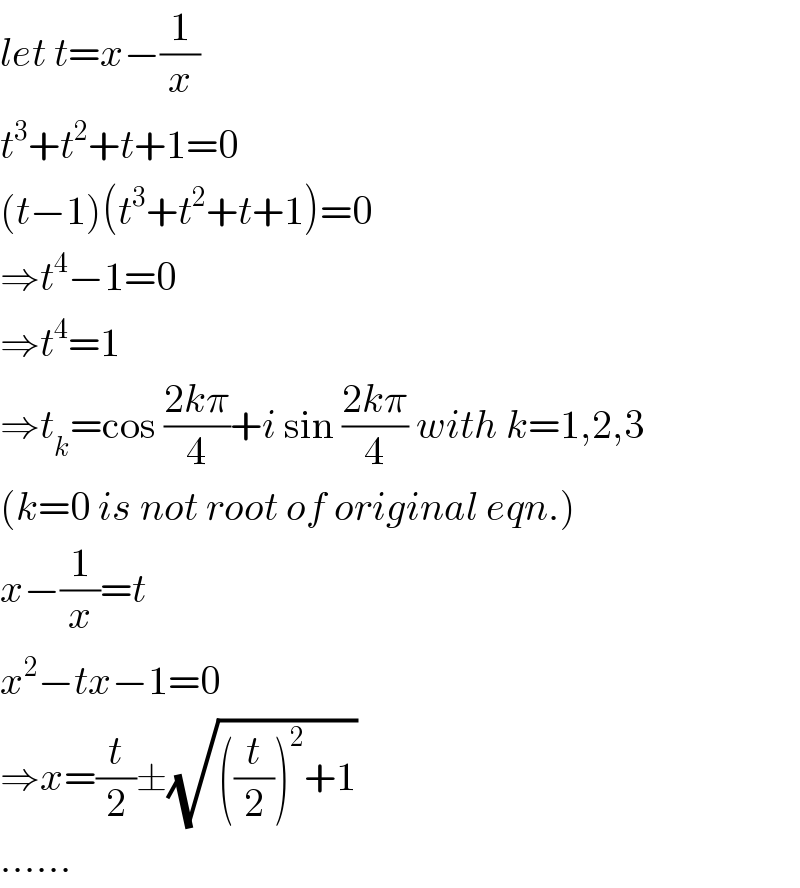
let t=x−(1/x) t^3 +t^2 +t+1=0 (t−1)(t^3 +t^2 +t+1)=0 ⇒t^4 −1=0 ⇒t^4 =1 ⇒t_k =cos ((2kπ)/4)+i sin ((2kπ)/4) with k=1,2,3 (k=0 is not root of original eqn.) x−(1/x)=t x^2 −tx−1=0 ⇒x=(t/2)±(√(((t/2))^2 +1)) ......
lett=x−1xt3+t2+t+1=0(t−1)(t3+t2+t+1)=0⇒t4−1=0⇒t4=1⇒tk=cos2kπ4+isin2kπ4withk=1,2,3(k=0isnotrootoforiginaleqn.)x−1x=tx2−tx−1=0⇒x=t2±(t2)2+1……
Answered by mathmax by abdo last updated on 30/May/20
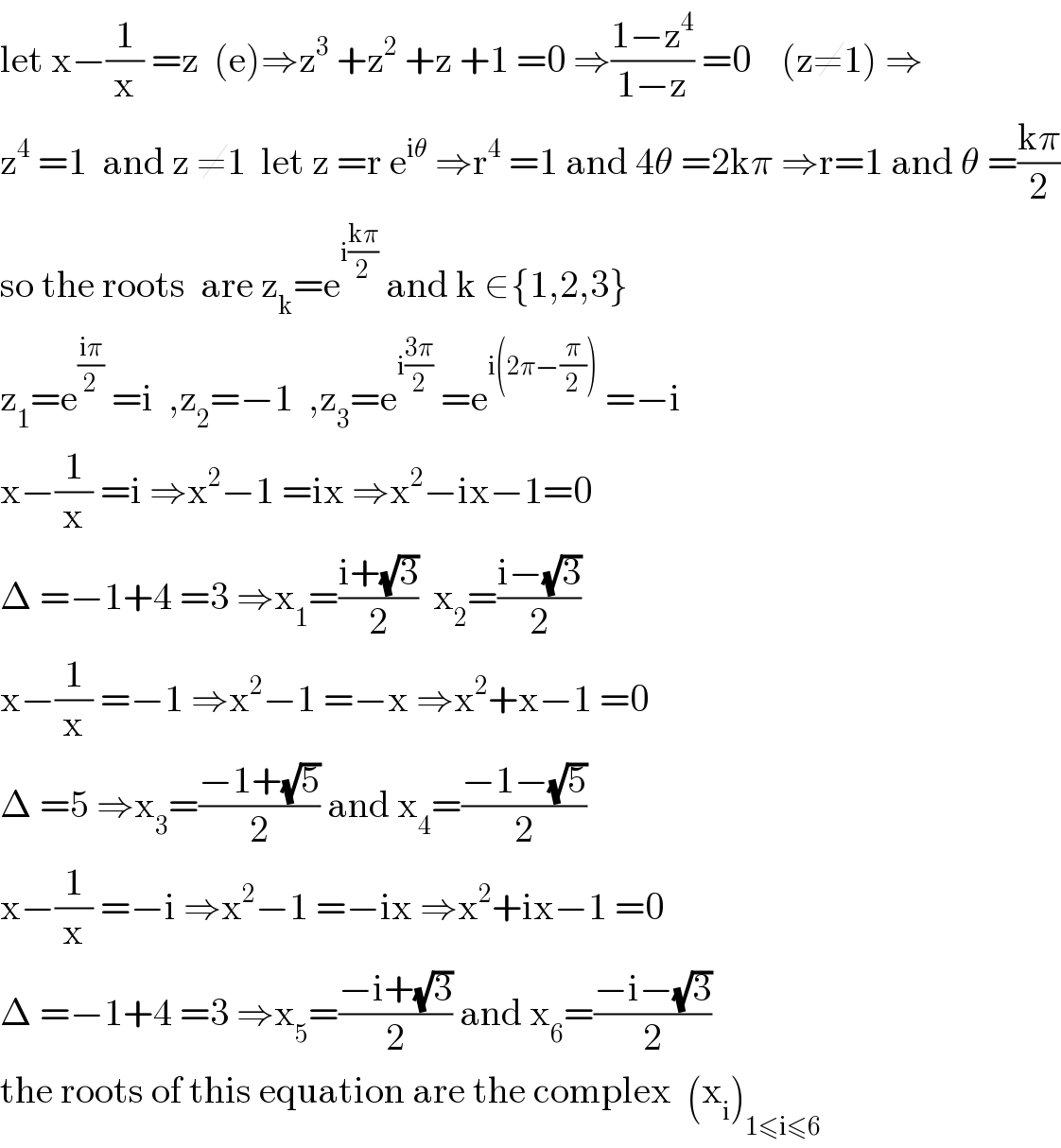
let x−(1/x) =z (e)⇒z^3 +z^2 +z +1 =0 ⇒((1−z^4 )/(1−z)) =0 (z≠1) ⇒ z^4 =1 and z ≠1 let z =r e^(iθ) ⇒r^4 =1 and 4θ =2kπ ⇒r=1 and θ =((kπ)/2) so the roots are z_k =e^(i((kπ)/2)) and k ∈{1,2,3} z_1 =e^((iπ)/2) =i ,z_2 =−1 ,z_3 =e^(i((3π)/2)) =e^(i(2π−(π/2))) =−i x−(1/x) =i ⇒x^2 −1 =ix ⇒x^2 −ix−1=0 Δ =−1+4 =3 ⇒x_1 =((i+(√3))/2) x_2 =((i−(√3))/2) x−(1/x) =−1 ⇒x^2 −1 =−x ⇒x^2 +x−1 =0 Δ =5 ⇒x_3 =((−1+(√5))/2) and x_4 =((−1−(√5))/2) x−(1/x) =−i ⇒x^2 −1 =−ix ⇒x^2 +ix−1 =0 Δ =−1+4 =3 ⇒x_5 =((−i+(√3))/2) and x_6 =((−i−(√3))/2) the roots of this equation are the complex (x_i )_(1≤i≤6)
letx−1x=z(e)⇒z3+z2+z+1=0⇒1−z41−z=0(z≠1)⇒z4=1andz≠1letz=reiθ⇒r4=1and4θ=2kπ⇒r=1andθ=kπ2sotherootsarezk=eikπ2andk∈{1,2,3}z1=eiπ2=i,z2=−1,z3=ei3π2=ei(2π−π2)=−ix−1x=i⇒x2−1=ix⇒x2−ix−1=0Δ=−1+4=3⇒x1=i+32x2=i−32x−1x=−1⇒x2−1=−x⇒x2+x−1=0Δ=5⇒x3=−1+52andx4=−1−52x−1x=−i⇒x2−1=−ix⇒x2+ix−1=0Δ=−1+4=3⇒x5=−i+32andx6=−i−32therootsofthisequationarethecomplex(xi)1⩽i⩽6
Answered by MJS last updated on 30/May/20
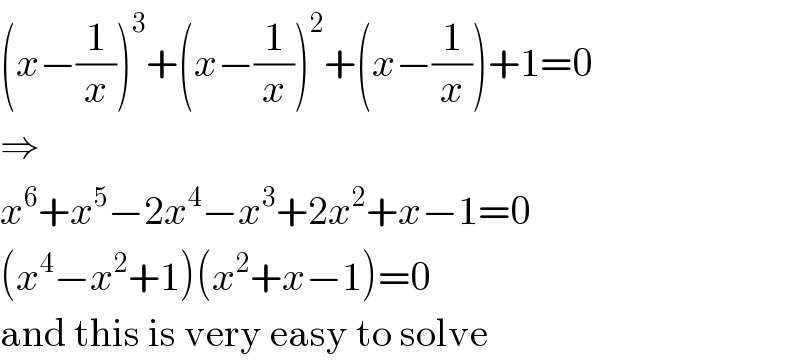
(x−(1/x))^3 +(x−(1/x))^2 +(x−(1/x))+1=0 ⇒ x^6 +x^5 −2x^4 −x^3 +2x^2 +x−1=0 (x^4 −x^2 +1)(x^2 +x−1)=0 and this is very easy to solve
(x−1x)3+(x−1x)2+(x−1x)+1=0⇒x6+x5−2x4−x3+2x2+x−1=0(x4−x2+1)(x2+x−1)=0andthisisveryeasytosolve
Commented by mr W last updated on 30/May/20
good idea!
goodidea!

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *