Question Number 61650 by maxmathsup by imad last updated on 05/Jun/19
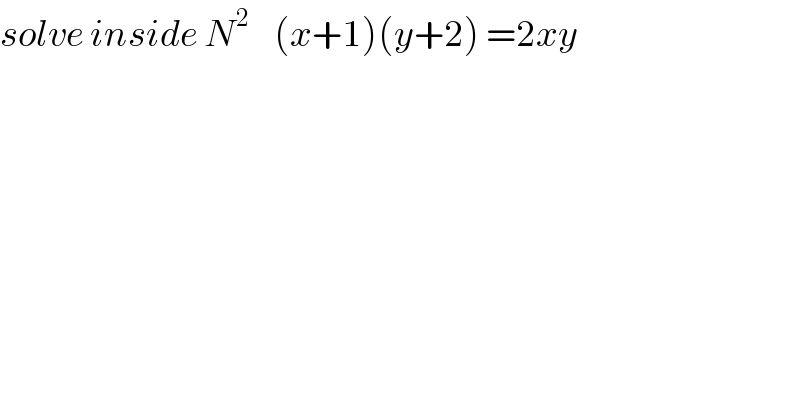
$${solve}\:{inside}\:{N}^{\mathrm{2}} \:\:\:\:\left({x}+\mathrm{1}\right)\left({y}+\mathrm{2}\right)\:=\mathrm{2}{xy} \\ $$
Commented by kaivan.ahmadi last updated on 06/Jun/19
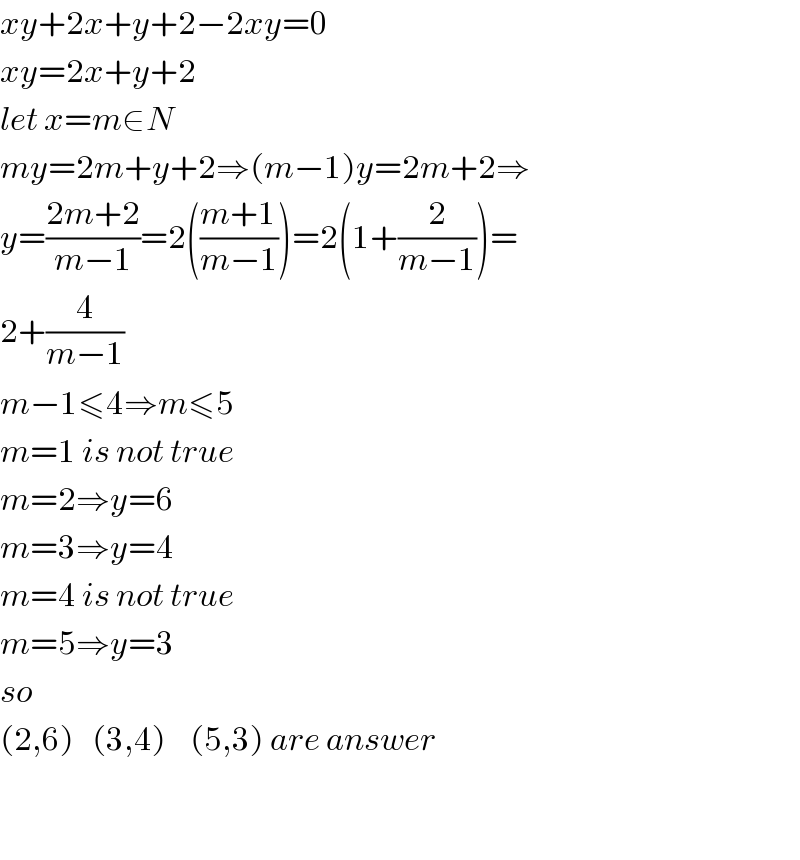
$${xy}+\mathrm{2}{x}+{y}+\mathrm{2}−\mathrm{2}{xy}=\mathrm{0} \\ $$$${xy}=\mathrm{2}{x}+{y}+\mathrm{2} \\ $$$${let}\:{x}={m}\in{N} \\ $$$${my}=\mathrm{2}{m}+{y}+\mathrm{2}\Rightarrow\left({m}−\mathrm{1}\right){y}=\mathrm{2}{m}+\mathrm{2}\Rightarrow \\ $$$${y}=\frac{\mathrm{2}{m}+\mathrm{2}}{{m}−\mathrm{1}}=\mathrm{2}\left(\frac{{m}+\mathrm{1}}{{m}−\mathrm{1}}\right)=\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{2}}{{m}−\mathrm{1}}\right)= \\ $$$$\mathrm{2}+\frac{\mathrm{4}}{{m}−\mathrm{1}} \\ $$$${m}−\mathrm{1}\leqslant\mathrm{4}\Rightarrow{m}\leqslant\mathrm{5} \\ $$$${m}=\mathrm{1}\:{is}\:{not}\:{true} \\ $$$${m}=\mathrm{2}\Rightarrow{y}=\mathrm{6} \\ $$$${m}=\mathrm{3}\Rightarrow{y}=\mathrm{4} \\ $$$${m}=\mathrm{4}\:{is}\:{not}\:{true} \\ $$$${m}=\mathrm{5}\Rightarrow{y}=\mathrm{3} \\ $$$${so}\: \\ $$$$\left(\mathrm{2},\mathrm{6}\right)\:\:\:\left(\mathrm{3},\mathrm{4}\right)\:\:\:\:\left(\mathrm{5},\mathrm{3}\right)\:{are}\:{answer} \\ $$$$ \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 06/Jun/19
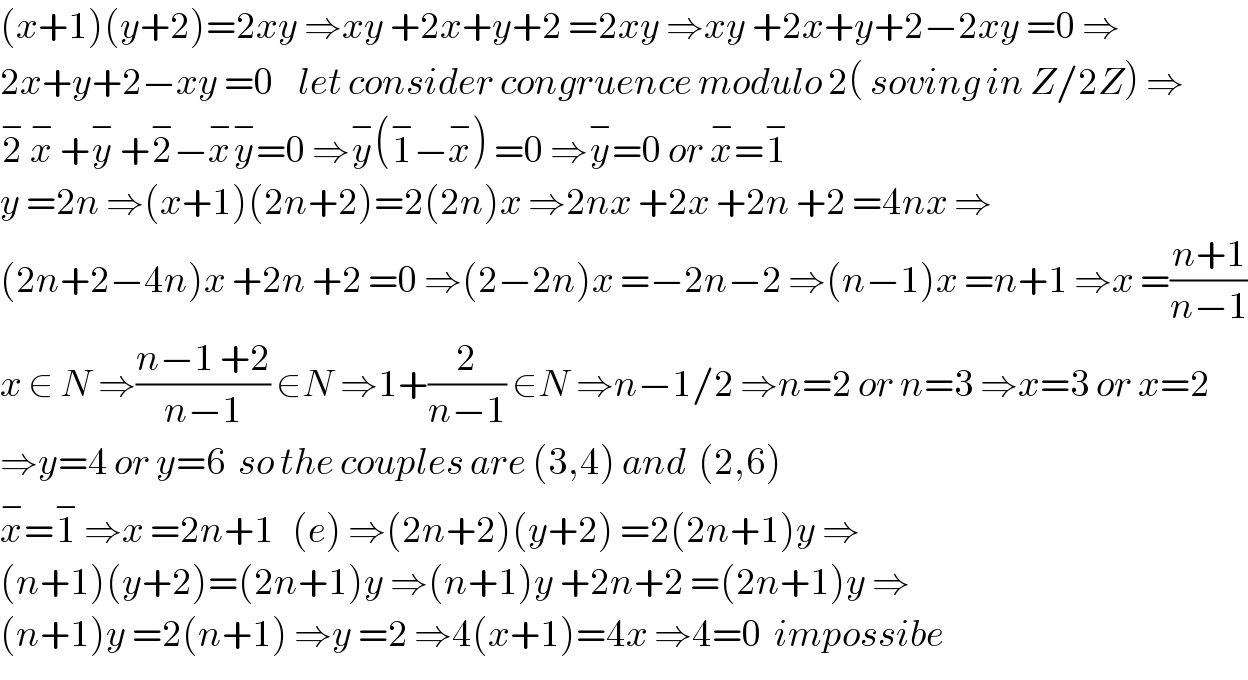
$$\left({x}+\mathrm{1}\right)\left({y}+\mathrm{2}\right)=\mathrm{2}{xy}\:\Rightarrow{xy}\:+\mathrm{2}{x}+{y}+\mathrm{2}\:=\mathrm{2}{xy}\:\Rightarrow{xy}\:+\mathrm{2}{x}+{y}+\mathrm{2}−\mathrm{2}{xy}\:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{2}{x}+{y}+\mathrm{2}−{xy}\:=\mathrm{0}\:\:\:\:{let}\:{consider}\:{congruence}\:{modulo}\:\mathrm{2}\left(\:{soving}\:{in}\:{Z}/\mathrm{2}{Z}\right)\:\Rightarrow \\ $$$$\overset{−} {\mathrm{2}}\:\overset{−} {{x}}\:+\overset{−} {{y}}\:+\overset{−} {\mathrm{2}}−\overset{−} {{x}}\overset{−} {{y}}=\mathrm{0}\:\Rightarrow\overset{−} {{y}}\left(\overset{−} {\mathrm{1}}−\overset{−} {{x}}\right)\:=\mathrm{0}\:\Rightarrow\overset{−} {{y}}=\mathrm{0}\:{or}\:\overset{−} {{x}}=\overset{−} {\mathrm{1}} \\ $$$${y}\:=\mathrm{2}{n}\:\Rightarrow\left({x}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{2}\right)=\mathrm{2}\left(\mathrm{2}{n}\right){x}\:\Rightarrow\mathrm{2}{nx}\:+\mathrm{2}{x}\:+\mathrm{2}{n}\:+\mathrm{2}\:=\mathrm{4}{nx}\:\Rightarrow \\ $$$$\left(\mathrm{2}{n}+\mathrm{2}−\mathrm{4}{n}\right){x}\:+\mathrm{2}{n}\:+\mathrm{2}\:=\mathrm{0}\:\Rightarrow\left(\mathrm{2}−\mathrm{2}{n}\right){x}\:=−\mathrm{2}{n}−\mathrm{2}\:\Rightarrow\left({n}−\mathrm{1}\right){x}\:={n}+\mathrm{1}\:\Rightarrow{x}\:=\frac{{n}+\mathrm{1}}{{n}−\mathrm{1}} \\ $$$${x}\:\in\:{N}\:\Rightarrow\frac{{n}−\mathrm{1}\:+\mathrm{2}}{{n}−\mathrm{1}}\:\in{N}\:\Rightarrow\mathrm{1}+\frac{\mathrm{2}}{{n}−\mathrm{1}}\:\in{N}\:\Rightarrow{n}−\mathrm{1}/\mathrm{2}\:\Rightarrow{n}=\mathrm{2}\:{or}\:{n}=\mathrm{3}\:\Rightarrow{x}=\mathrm{3}\:{or}\:{x}=\mathrm{2} \\ $$$$\Rightarrow{y}=\mathrm{4}\:{or}\:{y}=\mathrm{6}\:\:{so}\:{the}\:{couples}\:{are}\:\left(\mathrm{3},\mathrm{4}\right)\:{and}\:\:\left(\mathrm{2},\mathrm{6}\right) \\ $$$$\overset{−} {{x}}=\overset{−} {\mathrm{1}}\:\Rightarrow{x}\:=\mathrm{2}{n}+\mathrm{1}\:\:\:\left({e}\right)\:\Rightarrow\left(\mathrm{2}{n}+\mathrm{2}\right)\left({y}+\mathrm{2}\right)\:=\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right){y}\:\Rightarrow \\ $$$$\left({n}+\mathrm{1}\right)\left({y}+\mathrm{2}\right)=\left(\mathrm{2}{n}+\mathrm{1}\right){y}\:\Rightarrow\left({n}+\mathrm{1}\right){y}\:+\mathrm{2}{n}+\mathrm{2}\:=\left(\mathrm{2}{n}+\mathrm{1}\right){y}\:\Rightarrow \\ $$$$\left({n}+\mathrm{1}\right){y}\:=\mathrm{2}\left({n}+\mathrm{1}\right)\:\Rightarrow{y}\:=\mathrm{2}\:\Rightarrow\mathrm{4}\left({x}+\mathrm{1}\right)=\mathrm{4}{x}\:\Rightarrow\mathrm{4}=\mathrm{0}\:\:{impossibe}\: \\ $$
Commented by maxmathsup by imad last updated on 06/Jun/19
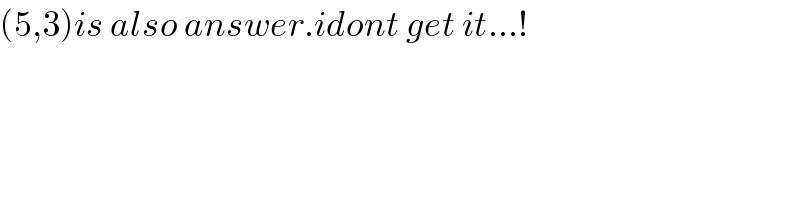
$$\left(\mathrm{5},\mathrm{3}\right){is}\:{also}\:{answer}.{idont}\:{get}\:{it}…! \\ $$
Commented by maxmathsup by imad last updated on 06/Jun/19
$${thanks}\:{sir}\:{Ahmadi}. \\ $$
