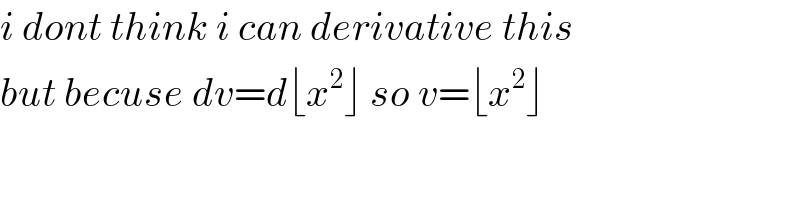solve-integration-1-2-x-d-x-2-

Question Number 85020 by M±th+et£s last updated on 18/Mar/20

s o l v e i n t e g r a t i o n

\int_{1}^{2} x d ⌊ x^{2} ⌋

Commented by mr W last updated on 18/Mar/20

1 ⩽ x < \sqrt{2} : ⌊ x^{2} ⌋ = 1, d (⌊ x^{2} ⌋) = 0 d x

\sqrt{2} ⩽ x < \sqrt{3} : ⌊ x^{2} ⌋ = 2, d (⌊ x^{2} ⌋) = 0 d x

\sqrt{3} ⩽ x < 2 : ⌊ x^{2} ⌋ = 3, d (⌊ x^{2} ⌋) = 0 d x

\int_{1}^{2} x d ⌊ x^{2} ⌋ = \int_{1}^{\sqrt{2}} x d ⌊ x^{2} ⌋ + \int_{\sqrt{2}}^{\sqrt{3}} x d ⌊ x^{2} ⌋ + \int_{\sqrt{3}}^{2} x d ⌊ x^{2} ⌋

= \int_{1}^{\sqrt{2}} x \times 0 d x + \int_{\sqrt{2}}^{\sqrt{3}} x \times 0 d x + \int_{\sqrt{3}}^{2} x \times 0 d x

= 0

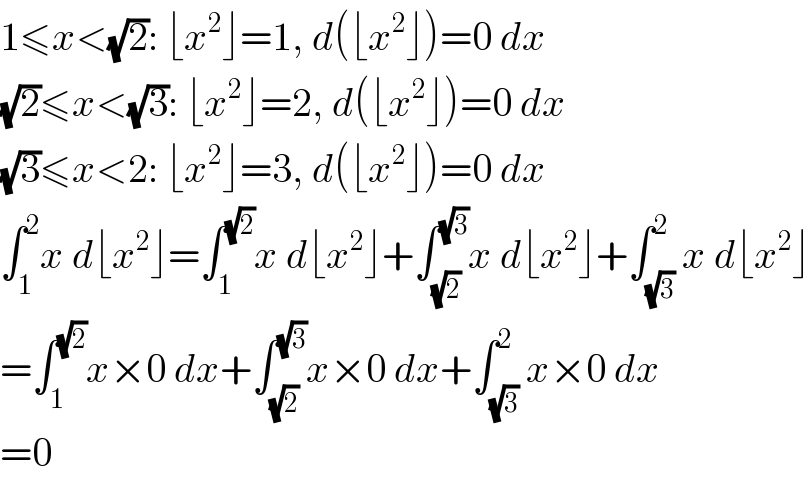
Commented by M±th+et£s last updated on 18/Mar/20

i t h i n k t h e s o l u t i o n i s 2 + \sqrt{3} + \sqrt{2}

u = x \to\to d u = d x

v = d ⌊ x^{2} ⌋ \to\to v = ⌊ x^{2} ⌋

I = {[⌊ x^{2} ⌋]}_{1}^{2} - \int_{1}^{2} ⌊ x^{2} ⌋ d x

(8 - 1) - [(\int_{1}^{\sqrt{2}} ⌊ x^{2} ⌋ d x + \int_{\sqrt{2}}^{\sqrt{3}} ⌊ x^{2} ⌋ d x + \int_{\sqrt{3}}^{2} ⌊ x^{2} ⌋ d x)]

7 - [{[1]}_{1}^{\sqrt{2}} + {[2]}_{\sqrt{2}}^{\sqrt{3}} + {[3]}_{\sqrt{3}}^{\sqrt{2}}]

7 - [\sqrt{2} - 1 + 2 (\sqrt{3} - \sqrt{2}) + 3 (2 - \sqrt{3})]

7 - [- \sqrt{2} - \sqrt{3} + 5]

2 + \sqrt{3} + \sqrt{2}

Commented by mr W last updated on 18/Mar/20

i f f (x) = ⌊ x^{2} ⌋, s a y 1 ⩽ x < \sqrt{2},

w h a t i s \frac{d f (x)}{d x} = ?

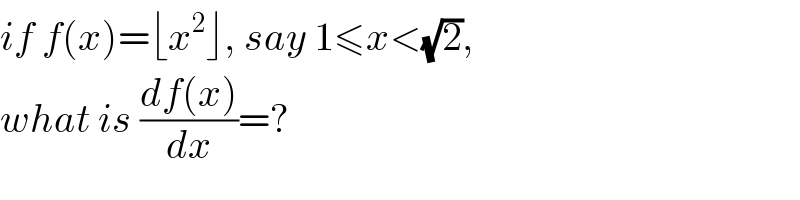
Commented by M±th+et£s last updated on 18/Mar/20

i d o n t t h i n k i c a n d e r i v a t i v e t h i s

b u t b e c u s e d v = d ⌊ x^{2} ⌋ s o v = ⌊ x^{2} ⌋