Question Number 152601 by mnjuly1970 last updated on 30/Aug/21
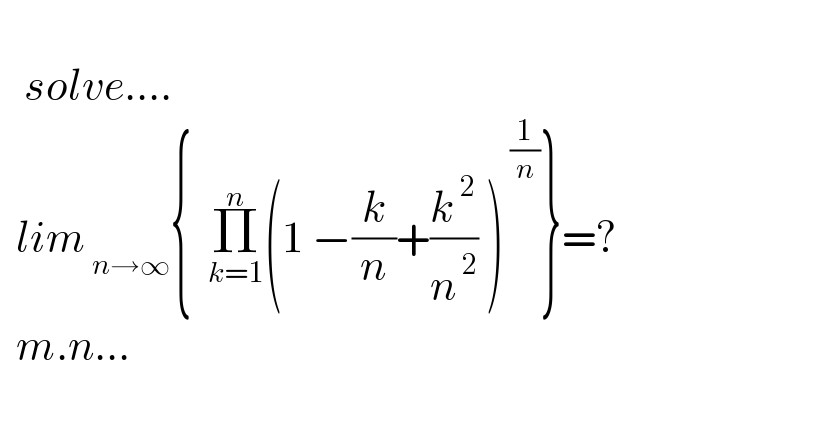
$$ \\ $$$$\:\:\:{solve}…. \\ $$$$\:\:{lim}_{\:{n}\rightarrow\infty} \left\{\:\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{1}\:−\frac{{k}}{{n}}+\frac{{k}^{\:\mathrm{2}} }{{n}^{\:\mathrm{2}} }\:\right)^{\:\frac{\mathrm{1}}{{n}}} \right\}=? \\ $$$$\:\:{m}.{n}… \\ $$$$ \\ $$
Commented by mindispower last updated on 30/Aug/21
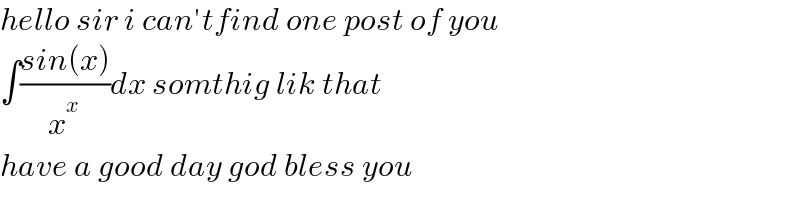
$${hello}\:{sir}\:{i}\:{can}'{tfind}\:{one}\:{post}\:{of}\:{you} \\ $$$$\int\frac{{sin}\left({x}\right)}{{x}^{{x}} }{dx}\:{somthig}\:{lik}\:{that} \\ $$$${have}\:{a}\:{good}\:{day}\:{god}\:{bless}\:{you} \\ $$
Answered by puissant last updated on 30/Aug/21
![U_n =Π_(k=1) ^n (1−(k/n)+(k^2 /n^2 ))^(1/n) V_n =ln(U_n ) ⇒ lim_(n→∞) V_n = lim_(n→∞) (1/n)Σ_(k=1) ^n ln(1−(k/n)+(k^2 /n^2 )) =∫_0 ^1 ln(1−x+x^2 )dx { ((u=ln(1−x+x^2 ))),((v′=1)) :} ⇒ { ((u′=((2x−1)/(1−x+x^2 )))),((v=x)) :} =[xln(1−x+x^2 )]_0 ^1 −∫_0 ^1 ((2x^2 −x)/(1−x+x^2 ))dx To be continued...](https://www.tinkutara.com/question/Q152603.png)
$${U}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{1}−\frac{{k}}{{n}}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$$ \\ $$$${V}_{{n}} ={ln}\left({U}_{{n}} \right) \\ $$$$\Rightarrow\:{lim}_{{n}\rightarrow\infty} {V}_{{n}} =\:{lim}_{{n}\rightarrow\infty} \frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{ln}\left(\mathrm{1}−\frac{{k}}{{n}}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right){dx} \\ $$$$\begin{cases}{{u}={ln}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)}\\{{v}'=\mathrm{1}}\end{cases}\:\Rightarrow\:\begin{cases}{{u}'=\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }}\\{{v}={x}}\end{cases} \\ $$$$=\left[{xln}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}^{\mathrm{2}} −{x}}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{dx} \\ $$$${To}\:{be}\:{continued}… \\ $$
Commented by SANOGO last updated on 30/Aug/21
$${merci}\:{bien}\:{mon}\:{prof} \\ $$
Commented by puissant last updated on 30/Aug/21

$${je}\:{suis}\:{pas}\:{prof}\:{broo}\:{je}\:{suis}\:\acute {{e}l}\grave {{e}ve}.. \\ $$
Commented by Ar Brandon last updated on 30/Aug/21

$$\ast\mathrm{etudiant}\: \\ $$😜
Answered by Olaf_Thorendsen last updated on 30/Aug/21
![∫_0 ^1 ln(1−x(1−x)) dx = lim_(n→∞) (1/n)Σ_(k=0) ^n ln(1−(k/n)+(k^2 /n^2 )) ∫_0 ^1 ln(1−x(1−x)) dx = [xln(1−x+x^2 )−2x−(1/2)ln(1−x+x^2 ) +(√3)arctan(((2x−1)/( (√3))))]_0 ^1 = 2(√3)arctan((1/( (√3))))−2 lim_(n→∞) Π_(k=1) ^n ln(1−(k/n)+(k^2 /n^2 ))^(1/n) = e^(2(√3)arctan((1/( (√3))))−2)](https://www.tinkutara.com/question/Q152604.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}−{x}\left(\mathrm{1}−{x}\right)\right)\:{dx}\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}−\frac{{k}}{{n}}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}−{x}\left(\mathrm{1}−{x}\right)\right)\:{dx}\:= \\ $$$$\left[{x}\mathrm{ln}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)−\mathrm{2}{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)\right. \\ $$$$\left.+\sqrt{\mathrm{3}}\mathrm{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\:\mathrm{2}\sqrt{\mathrm{3}}\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)−\mathrm{2} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\mathrm{ln}\left(\mathrm{1}−\frac{{k}}{{n}}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{{n}}} \:=\:{e}^{\mathrm{2}\sqrt{\mathrm{3}}\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)−\mathrm{2}} \\ $$
Commented by SANOGO last updated on 30/Aug/21
$${merci}\:{bien}\:{mon}\:{prof}\: \\ $$
Commented by mnjuly1970 last updated on 30/Aug/21
$$\:{thanks}\:{alot}\:{mr}\:{olaf}… \\ $$
