solve-lim-n-n-2-ln-n-sin-1-n-

Question Number 167624 by mnjuly1970 last updated on 21/Mar/22

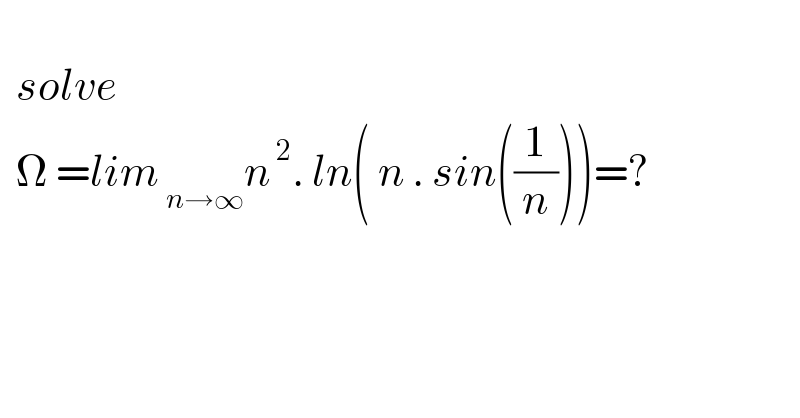
solve Ω =lim_( n→∞) n^( 2) . ln( n . sin((1/n)))=?

$$ \\ $$$$\:\:{solve} \\ $$$$\:\:\Omega\:={lim}_{\:{n}\rightarrow\infty} {n}^{\:\mathrm{2}} .\:{ln}\left(\:{n}\:.\:{sin}\left(\frac{\mathrm{1}}{{n}}\right)\right)=? \\ $$$$ \\ $$

Answered by qaz last updated on 21/Mar/22

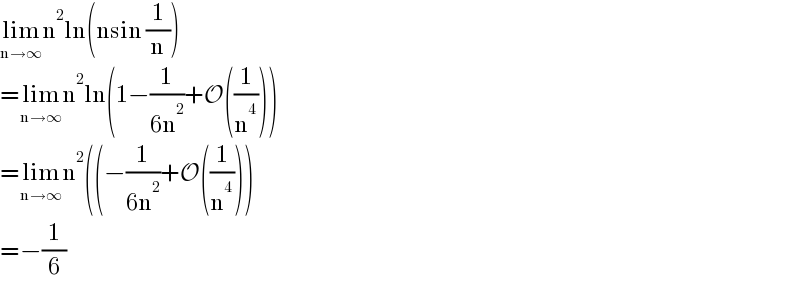
lim_(n→∞) n^2 ln(nsin (1/n)) =lim_(n→∞) n^2 ln(1−(1/(6n^2 ))+O((1/n^4 ))) =lim_(n→∞) n^2 ((−(1/(6n^2 ))+O((1/n^4 ))) =−(1/6)

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}n}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{nsin}\:\frac{\mathrm{1}}{\mathrm{n}}\right) \\ $$$$=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}n}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6n}^{\mathrm{2}} }+\mathcal{O}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{4}} }\right)\right) \\ $$$$=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}n}^{\mathrm{2}} \left(\left(−\frac{\mathrm{1}}{\mathrm{6n}^{\mathrm{2}} }+\mathcal{O}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{4}} }\right)\right)\right. \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}} \\ $$

Commented by mnjuly1970 last updated on 22/Mar/22

$$\checkmark \\ $$

Answered by LEKOUMA last updated on 21/Mar/22

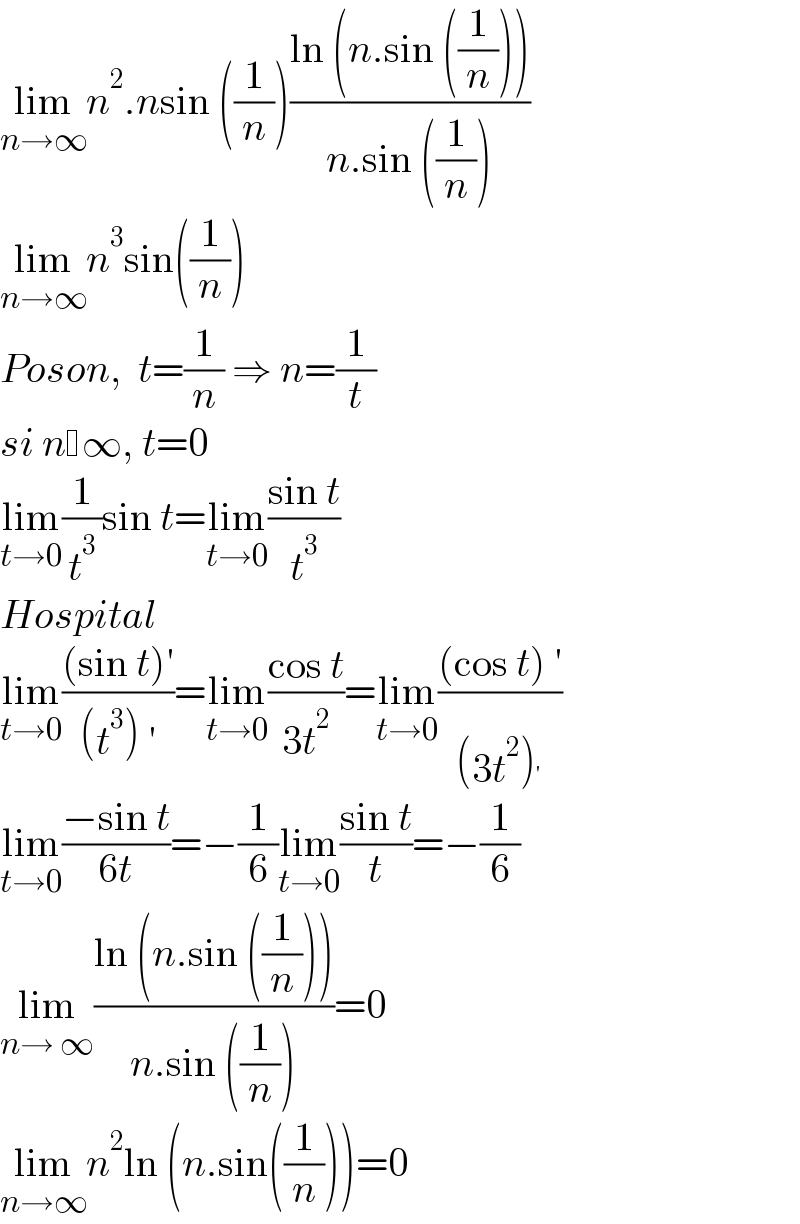
lim_(n→∞) n^2 .nsin ((1/n))((ln (n.sin ((1/n))))/(n.sin ((1/n)))) lim_(n→∞) n^3 sin((1/n)) Poson, t=(1/n) ⇒ n=(1/t) si n ∞, t=0 lim_(t→0) (1/t^3 )sin t=lim_(t→0) ((sin t)/t^3 ) Hospital lim_(t→0) (((sin t)′)/((t^3 ) ′))=lim_(t→0) ((cos t)/(3t^2 ))=lim_(t→0) (((cos t) ′)/((3t^2 )^′ )) lim_(t→0) ((−sin t)/(6t))=−(1/6)lim_(t→0) ((sin t)/t)=−(1/6) lim_(n→ ∞) ((ln (n.sin ((1/n))))/(n.sin ((1/n))))=0 lim_(n→∞) n^2 ln (n.sin((1/n)))=0

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{n}^{\mathrm{2}} .{n}\mathrm{sin}\:\left(\frac{\mathrm{1}}{{n}}\right)\frac{\mathrm{ln}\:\left({n}.\mathrm{sin}\:\left(\frac{\mathrm{1}}{{n}}\right)\right)}{{n}.\mathrm{sin}\:\left(\frac{\mathrm{1}}{{n}}\right)} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{n}^{\mathrm{3}} \mathrm{sin}\left(\frac{\mathrm{1}}{{n}}\right) \\ $$$${Poson},\:\:{t}=\frac{\mathrm{1}}{{n}}\:\Rightarrow\:{n}=\frac{\mathrm{1}}{{t}} \\ $$$${si}\:{n} \infty,\:{t}=\mathrm{0} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\mathrm{sin}\:{t}=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{t}}{{t}^{\mathrm{3}} } \\ $$$${Hospital} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{sin}\:{t}\right)'}{\left({t}^{\mathrm{3}} \right)\:'}=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:{t}}{\mathrm{3}{t}^{\mathrm{2}} }=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{cos}\:{t}\right)\:'}{\left(\mathrm{3}{t}^{\mathrm{2}} \right)^{'} } \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{sin}\:{t}}{\mathrm{6}{t}}=−\frac{\mathrm{1}}{\mathrm{6}}\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{t}}{{t}}=−\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\underset{{n}\rightarrow\:\infty} {\mathrm{lim}}\frac{\mathrm{ln}\:\left({n}.\mathrm{sin}\:\left(\frac{\mathrm{1}}{{n}}\right)\right)}{{n}.\mathrm{sin}\:\left(\frac{\mathrm{1}}{{n}}\right)}=\mathrm{0} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{n}^{\mathrm{2}} \mathrm{ln}\:\left({n}.\mathrm{sin}\left(\frac{\mathrm{1}}{{n}}\right)\right)=\mathrm{0}\: \\ $$

Facebook Tweet Pin

solve-lim-n-n-2-ln-n-sin-1-n-

Leave a Reply Cancel reply