solve-lim-p-p-2-2-p-2-p-2-p-2-2-

Question Number 114299 by bemath last updated on 18/Sep/20

$$\:{solve}\:\underset{{p}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{{p}^{\mathrm{2}} +\mathrm{2}}{{p}+\mathrm{2}}\right)^{\frac{{p}+\mathrm{2}}{{p}^{\mathrm{2}} +\mathrm{2}}} \:? \\ $$

Commented by mohammad17 last updated on 18/Sep/20

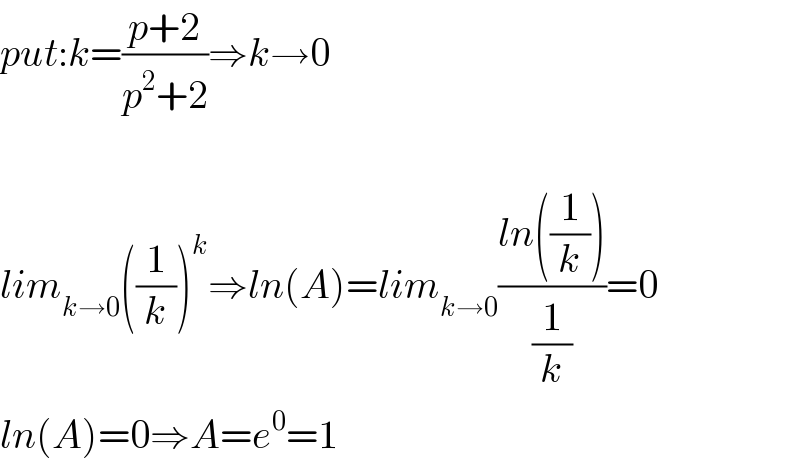
put:k=((p+2)/(p^2 +2))⇒k→0 lim_(k→0) ((1/k))^k ⇒ln(A)=lim_(k→0) ((ln((1/k)))/(1/k))=0 ln(A)=0⇒A=e^0 =1

$${put}:{k}=\frac{{p}+\mathrm{2}}{{p}^{\mathrm{2}} +\mathrm{2}}\Rightarrow{k}\rightarrow\mathrm{0} \\ $$$$ \\ $$$${lim}_{{k}\rightarrow\mathrm{0}} \left(\frac{\mathrm{1}}{{k}}\right)^{{k}} \Rightarrow{ln}\left({A}\right)={lim}_{{k}\rightarrow\mathrm{0}} \frac{{ln}\left(\frac{\mathrm{1}}{{k}}\right)}{\frac{\mathrm{1}}{{k}}}=\mathrm{0} \\ $$$${ln}\left({A}\right)=\mathrm{0}\Rightarrow{A}={e}^{\mathrm{0}} =\mathrm{1} \\ $$

Answered by 1549442205PVT last updated on 18/Sep/20

I=lim (_(p→∞t) ((p^2 +2)/(p+2)))^((p+2)/(p^2 +2)) lnI=lim_(p→∞) [((p+2)/(p^2 +2))ln(((p^2 +2)/(p+2)))] =lim_(p→∞) ((ln(((p^2 +2)/(p+2))))/((p^2 +2)/(p+2))).This is the form(∞/∞) Applying L′Hopital rule we have lnI=lim_(p→∞) ((((p+2)/(p^2 +2))×((2p(p+2)−(p^2 +2))/((p+2)^2 )))/((2p(p+2)−(p^2 +2))/((p+2)^2 ))) =lim_(p→∞) ((p+2)/(p^2 +2))=0⇒I=e^0 =1

$$\mathrm{I}=\underset{\mathrm{p}\rightarrow\infty\mathrm{t}} {\mathrm{lim}\:\left(}\frac{{p}^{\mathrm{2}} +\mathrm{2}}{{p}+\mathrm{2}}\right)^{\frac{{p}+\mathrm{2}}{{p}^{\mathrm{2}} +\mathrm{2}}} \: \\ $$$$\mathrm{lnI}=\underset{\mathrm{p}\rightarrow\infty} {\mathrm{lim}}\left[\frac{\mathrm{p}+\mathrm{2}}{\mathrm{p}^{\mathrm{2}} +\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{p}^{\mathrm{2}} +\mathrm{2}}{\mathrm{p}+\mathrm{2}}\right)\right] \\ $$$$=\underset{\mathrm{p}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{ln}\left(\frac{\mathrm{p}^{\mathrm{2}} +\mathrm{2}}{\mathrm{p}+\mathrm{2}}\right)}{\frac{\mathrm{p}^{\mathrm{2}} +\mathrm{2}}{\mathrm{p}+\mathrm{2}}}.\mathrm{This}\:\mathrm{is}\:\mathrm{the}\:\mathrm{form}\frac{\infty}{\infty} \\ $$$$\mathrm{Applying}\:\mathrm{L}'\mathrm{Hopital}\:\mathrm{rule}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{lnI}=\underset{\mathrm{p}\rightarrow\infty} {\mathrm{lim}}\frac{\frac{\mathrm{p}+\mathrm{2}}{\mathrm{p}^{\mathrm{2}} +\mathrm{2}}×\frac{\mathrm{2p}\left(\mathrm{p}+\mathrm{2}\right)−\left(\mathrm{p}^{\mathrm{2}} +\mathrm{2}\right)}{\left(\mathrm{p}+\mathrm{2}\right)^{\mathrm{2}} }}{\frac{\mathrm{2p}\left(\mathrm{p}+\mathrm{2}\right)−\left(\mathrm{p}^{\mathrm{2}} +\mathrm{2}\right)}{\left(\mathrm{p}+\mathrm{2}\right)^{\mathrm{2}} }} \\ $$$$=\underset{\mathrm{p}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{p}+\mathrm{2}}{\mathrm{p}^{\mathrm{2}} +\mathrm{2}}=\mathrm{0}\Rightarrow\mathrm{I}=\mathrm{e}^{\mathrm{0}} =\mathrm{1} \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 19/Sep/20

let f(x) =(((x^2 +2)/(x+2)))^((x+2)/(x^2 +2)) ⇒f(x) =e^(((x+2)/(x^2 +2))ln(((x^2 +2)/(x+2))) ) we have at +∞ ((x+2)/(x^2 +2))ln(((x^2 +2)/(x+2)))∼(1/x)ln(x)→0 ⇒lim_(x→+∞) f(x)=e^0 =1 =

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\left(\frac{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}}{\mathrm{x}+\mathrm{2}}\right)^{\frac{\mathrm{x}+\mathrm{2}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\mathrm{x}+\mathrm{2}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}}{\mathrm{x}+\mathrm{2}}\right)\:} \:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{at}\:+\infty\:\:\:\frac{\mathrm{x}+\mathrm{2}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}}{\mathrm{x}+\mathrm{2}}\right)\sim\frac{\mathrm{1}}{\mathrm{x}}\mathrm{ln}\left(\mathrm{x}\right)\rightarrow\mathrm{0}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{\mathrm{0}} \:=\mathrm{1} \\ $$$$= \\ $$

Facebook Tweet Pin

solve-lim-p-p-2-2-p-2-p-2-p-2-2-

Leave a Reply Cancel reply