Question Number 172081 by Mikenice last updated on 23/Jun/22
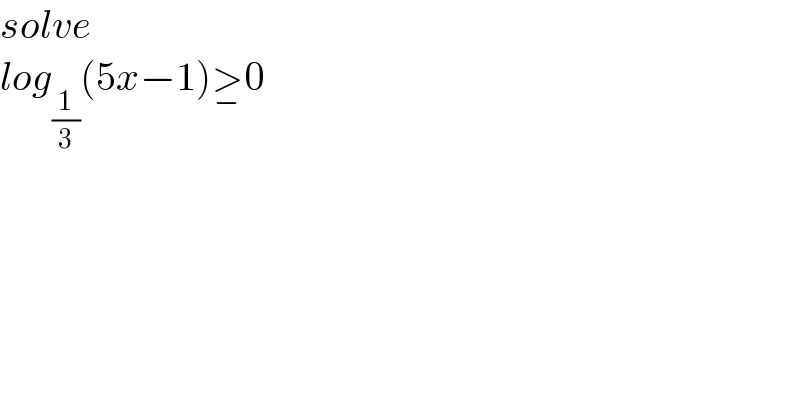
$${solve} \\ $$$${log}_{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{5}{x}−\mathrm{1}\right)\underset{−} {>}\mathrm{0} \\ $$
Commented by mr W last updated on 23/Jun/22

$$\mathrm{5}{x}−\mathrm{1}\geqslant\mathrm{1} \\ $$$$\Rightarrow{x}\geqslant\frac{\mathrm{2}}{\mathrm{5}} \\ $$
Commented by mr W last updated on 23/Jun/22
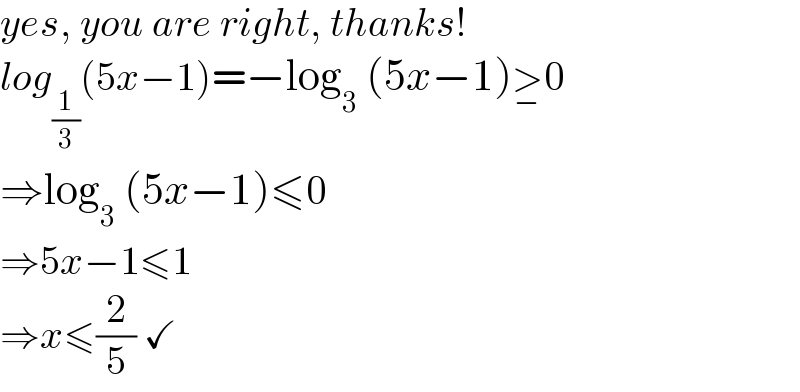
$${yes},\:{you}\:{are}\:{right},\:{thanks}! \\ $$$${log}_{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{5}{x}−\mathrm{1}\right)=−\mathrm{log}_{\mathrm{3}} \:\left(\mathrm{5}{x}−\mathrm{1}\right)\underset{−} {>}\mathrm{0} \\ $$$$\Rightarrow\mathrm{log}_{\mathrm{3}} \:\left(\mathrm{5}{x}−\mathrm{1}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{5}{x}−\mathrm{1}\leqslant\mathrm{1} \\ $$$$\Rightarrow{x}\leqslant\frac{\mathrm{2}}{\mathrm{5}}\:\checkmark \\ $$
