Solve-log-r-8-log-3-p-5-i-r-p-11-ii-

Question Number 104086 by I want to learn more last updated on 19/Jul/20

Solve : \log_{r} 8 + \log_{3} p = 5 \dots . . (i)

r + p = 11 \dots . . (ii)

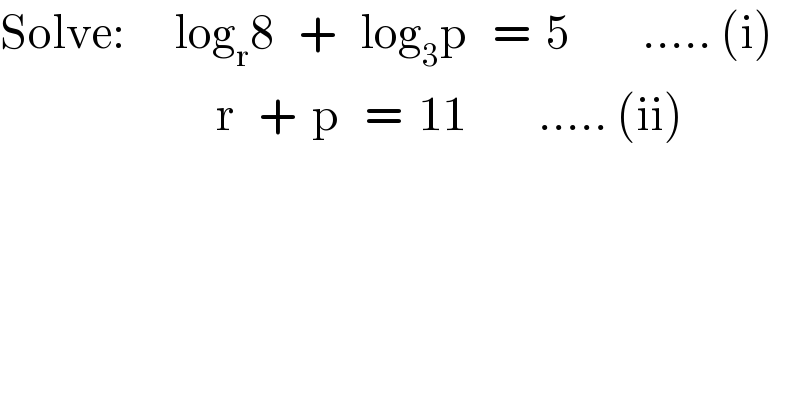
Commented by I want to learn more last updated on 19/Jul/20

Yes sir, but it is the workings i {don}^{'} t know sir .

Commented by mr W last updated on 19/Jul/20

i “ {s e e}^{″} t h e s o l u t i o n r = 2, p = 9 .

i t i s e x p e c t e d t h a t y o u c a n s e e t h e

s o l u t i o n, n o t c a l c u l a t e . i f t h e s e c o n d

e q n . i s r + p = 12, y o u c a n n o t s e e a n d

a l s o n o t c a l c u l a t e t h e s o l u t i o n .

Commented by I want to learn more last updated on 19/Jul/20

Alright . Thanks sir .

Answered by 1549442205PVT last updated on 19/Jul/20

Put \log_{r} 8 = a, \log_{3} p = b . We get

8 = r^{a}, p = 3^{b} (r > 0, r \neq 1, p > 0)

{\begin{cases} a + b = 5 (1) \\ 3^{b} + 8^{\frac{1}{a}} = 11 (2) \end{cases}

From (1) we get b = 5 - a, replace into

(2) we get 3^{5 - a} + 8^{\frac{1}{a}} - 11 = 0 (1) . we need to

have r = 8^{\frac{1}{a}} < 11 \Rightarrow a > \frac{\ln 8}{\ln 11} \approx 0.8671 .

Putting f (a) = 3^{5 - a} + 8^{\frac{1}{a}} - 11 . It is easy to see

that f (3) = 0, so a = 3 is root of eqs . (1)

we will prove it is unique root . Indeed,

f^{'} (a) = - \ln 3 \times 3^{5 - a} + 8^{\frac{1}{a}} (- \frac{1}{a^{2}}) < 0 \forall a \in (\frac{\ln 8}{\ln 11}; + \infty)

hence a = 3 is unique root of eqs . (1)

\Rightarrow b = 2 . From that we get r = 2, p = 9

Commented by I want to learn more last updated on 19/Jul/20

I appreciate sir .