Question Number 164328 by mnjuly1970 last updated on 16/Jan/22
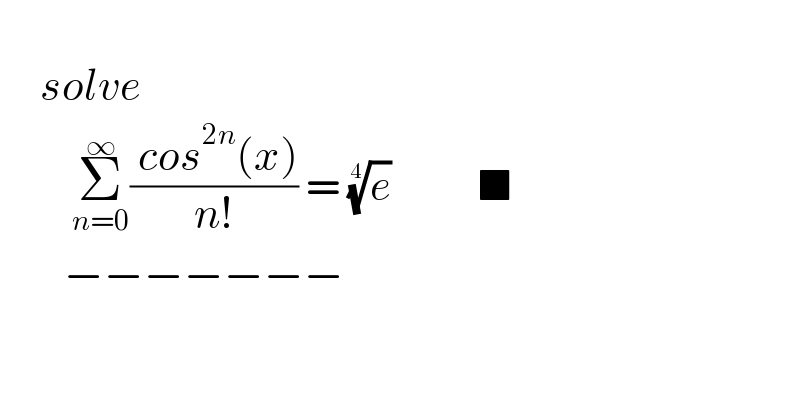
$$ \\ $$$$\:\:\:\:\:{solve} \\ $$$$\:\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\:{cos}^{\mathrm{2}{n}} \left({x}\right)}{{n}!}\:=\:\sqrt[{\mathrm{4}}]{{e}}\:\:\:\:\:\:\:\:\:\:\:\blacksquare\: \\ $$$$\:\:\:\:\:\:\:\:−−−−−−− \\ $$$$\:\: \\ $$
Answered by qaz last updated on 16/Jan/22
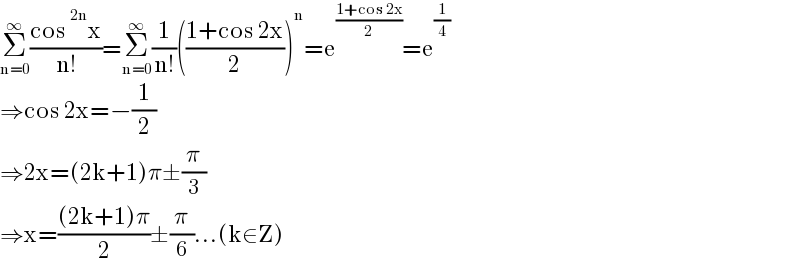
$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{cos}\:^{\mathrm{2n}} \mathrm{x}}{\mathrm{n}!}=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}!}\left(\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2x}}{\mathrm{2}}\right)^{\mathrm{n}} =\mathrm{e}^{\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2x}}{\mathrm{2}}} =\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{2x}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2x}=\left(\mathrm{2k}+\mathrm{1}\right)\pi\pm\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{x}=\frac{\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{2}}\pm\frac{\pi}{\mathrm{6}}…\left(\mathrm{k}\in\mathrm{Z}\right) \\ $$
Answered by Lordose last updated on 16/Jan/22
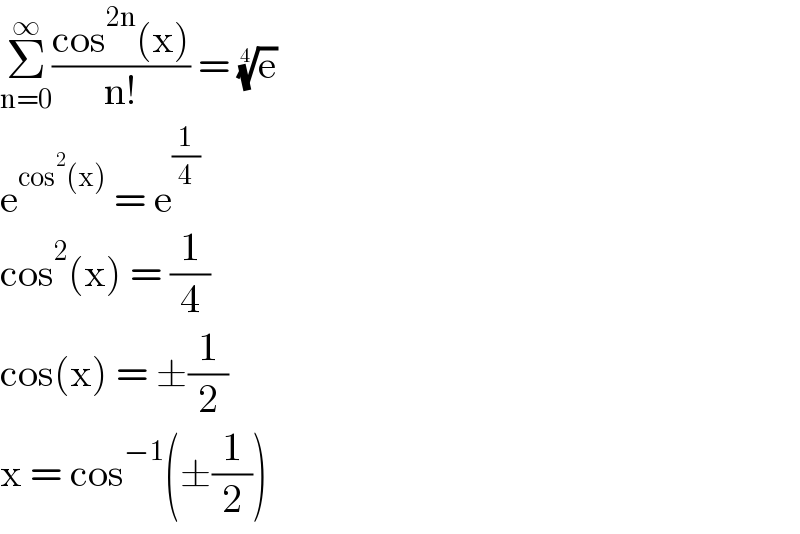
$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{cos}^{\mathrm{2n}} \left(\mathrm{x}\right)}{\mathrm{n}!}\:=\:\sqrt[{\mathrm{4}}]{\mathrm{e}} \\ $$$$\mathrm{e}^{\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)} \:=\:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{cos}\left(\mathrm{x}\right)\:=\:\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{x}\:=\:\mathrm{cos}^{−\mathrm{1}} \left(\pm\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$
