Question Number 42528 by rahul 19 last updated on 27/Aug/18
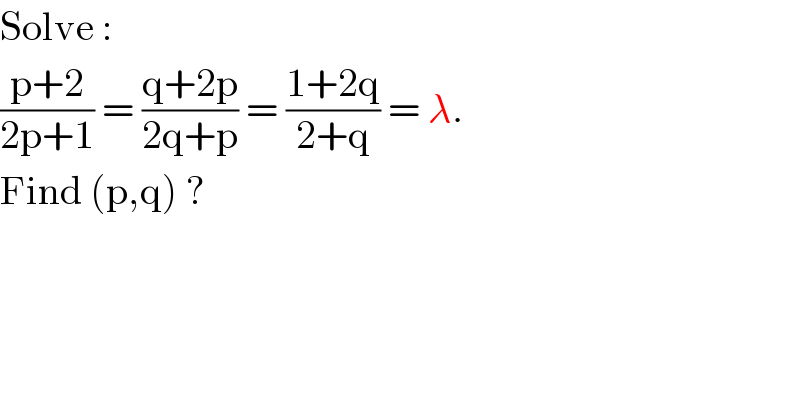
$$\mathrm{Solve}\:: \\ $$$$\frac{\mathrm{p}+\mathrm{2}}{\mathrm{2p}+\mathrm{1}}\:=\:\frac{\mathrm{q}+\mathrm{2p}}{\mathrm{2q}+\mathrm{p}}\:=\:\frac{\mathrm{1}+\mathrm{2q}}{\mathrm{2}+\mathrm{q}}\:=\:\lambda. \\ $$$$\mathrm{Find}\:\left(\mathrm{p},\mathrm{q}\right)\:? \\ $$
Answered by math1967 last updated on 27/Aug/18
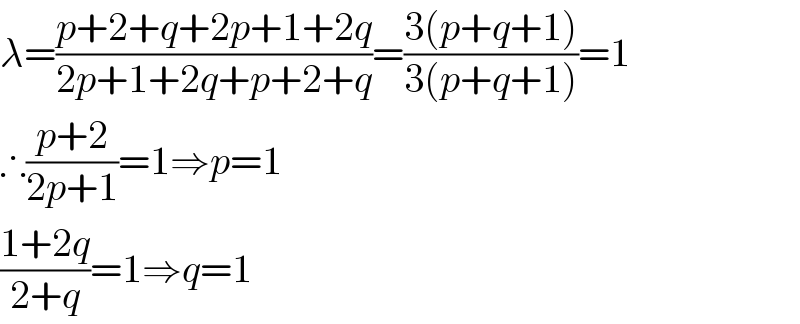
$$\lambda=\frac{{p}+\mathrm{2}+{q}+\mathrm{2}{p}+\mathrm{1}+\mathrm{2}{q}}{\mathrm{2}{p}+\mathrm{1}+\mathrm{2}{q}+{p}+\mathrm{2}+{q}}=\frac{\mathrm{3}\left({p}+{q}+\mathrm{1}\right)}{\mathrm{3}\left({p}+{q}+\mathrm{1}\right)}=\mathrm{1} \\ $$$$\therefore\frac{{p}+\mathrm{2}}{\mathrm{2}{p}+\mathrm{1}}=\mathrm{1}\Rightarrow{p}=\mathrm{1} \\ $$$$\frac{\mathrm{1}+\mathrm{2}{q}}{\mathrm{2}+{q}}=\mathrm{1}\Rightarrow{q}=\mathrm{1} \\ $$
Commented by rahul 19 last updated on 31/Aug/18
thanks sir!
