Question Number 151114 by mnjuly1970 last updated on 18/Aug/21
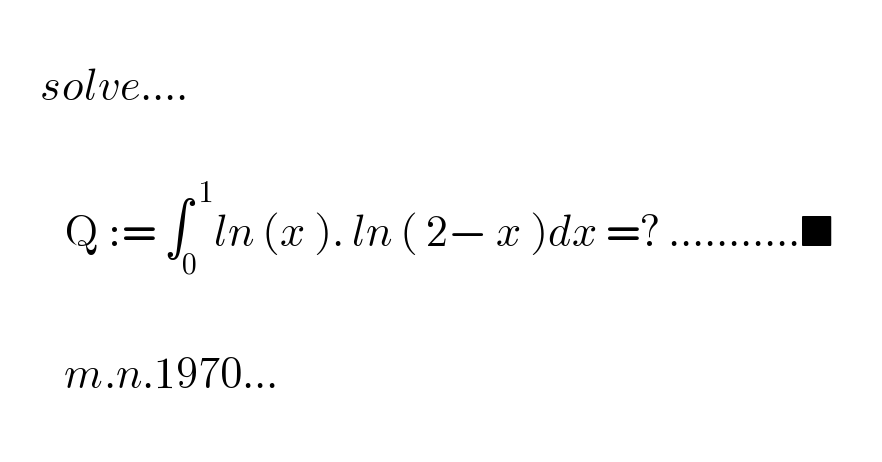
$$ \\ $$$$\:\:\:\:\:{solve}…. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\mathrm{Q}\::=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\:\left({x}\:\right).\:{ln}\:\left(\:\mathrm{2}−\:{x}\:\right){dx}\:=?\:………..\blacksquare \\ $$$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:{m}.{n}.\mathrm{1970}… \\ $$$$ \\ $$
Answered by qaz last updated on 18/Aug/21
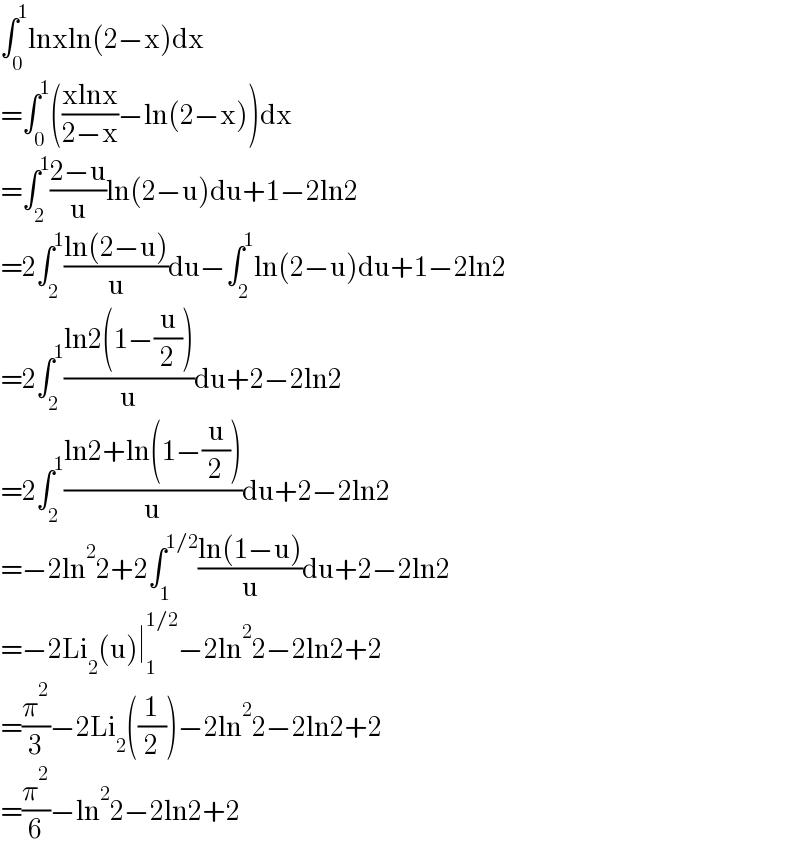
$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{lnxln}\left(\mathrm{2}−\mathrm{x}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{xlnx}}{\mathrm{2}−\mathrm{x}}−\mathrm{ln}\left(\mathrm{2}−\mathrm{x}\right)\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{2}} ^{\mathrm{1}} \frac{\mathrm{2}−\mathrm{u}}{\mathrm{u}}\mathrm{ln}\left(\mathrm{2}−\mathrm{u}\right)\mathrm{du}+\mathrm{1}−\mathrm{2ln2} \\ $$$$=\mathrm{2}\int_{\mathrm{2}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{2}−\mathrm{u}\right)}{\mathrm{u}}\mathrm{du}−\int_{\mathrm{2}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{2}−\mathrm{u}\right)\mathrm{du}+\mathrm{1}−\mathrm{2ln2} \\ $$$$=\mathrm{2}\int_{\mathrm{2}} ^{\mathrm{1}} \frac{\mathrm{ln2}\left(\mathrm{1}−\frac{\mathrm{u}}{\mathrm{2}}\right)}{\mathrm{u}}\mathrm{du}+\mathrm{2}−\mathrm{2ln2} \\ $$$$=\mathrm{2}\int_{\mathrm{2}} ^{\mathrm{1}} \frac{\mathrm{ln2}+\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{u}}{\mathrm{2}}\right)}{\mathrm{u}}\mathrm{du}+\mathrm{2}−\mathrm{2ln2} \\ $$$$=−\mathrm{2ln}^{\mathrm{2}} \mathrm{2}+\mathrm{2}\int_{\mathrm{1}} ^{\mathrm{1}/\mathrm{2}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{u}\right)}{\mathrm{u}}\mathrm{du}+\mathrm{2}−\mathrm{2ln2} \\ $$$$=−\mathrm{2Li}_{\mathrm{2}} \left(\mathrm{u}\right)\mid_{\mathrm{1}} ^{\mathrm{1}/\mathrm{2}} −\mathrm{2ln}^{\mathrm{2}} \mathrm{2}−\mathrm{2ln2}+\mathrm{2} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{3}}−\mathrm{2Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2ln}^{\mathrm{2}} \mathrm{2}−\mathrm{2ln2}+\mathrm{2} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{ln}^{\mathrm{2}} \mathrm{2}−\mathrm{2ln2}+\mathrm{2} \\ $$
Commented by mnjuly1970 last updated on 18/Aug/21

$$\:\:{excellent}\:{master}\:{qazi}… \\ $$
