Menu Close

Solve-quadratic-equation-about-t-1-h-v-0-t-1-2-gt-2-2-x-v-0-t-1-2-at-2-solve-v-v-2-v-0-2-2ax-

Tinku Tara 0 Comments
Pin




Question Number 170546 by libaolin last updated on 26/May/22
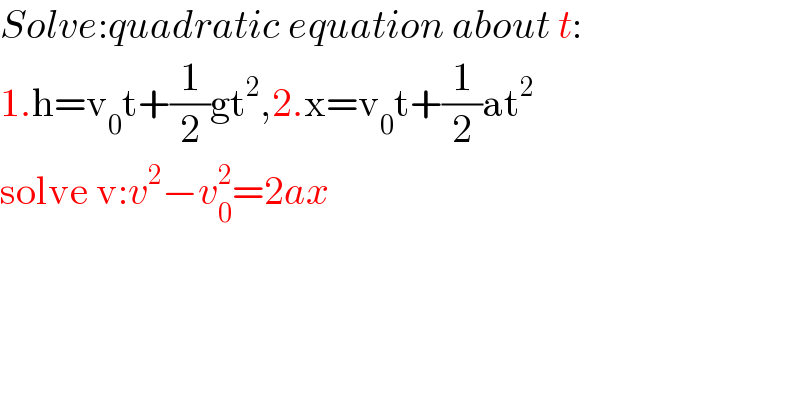
Solve:quadratic equation about t: 1.h=v_0 t+(1/2)gt^2 ,2.x=v_0 t+(1/2)at^2 solve v:v^2 −v_0 ^2 =2ax
$${Solve}:{quadratic}\:{equation}\:{about}\:{t}: \\ $$$$\mathrm{1}.\mathrm{h}=\mathrm{v}_{\mathrm{0}} \mathrm{t}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{gt}^{\mathrm{2}} ,\mathrm{2}.\mathrm{x}=\mathrm{v}_{\mathrm{0}} \mathrm{t}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{at}^{\mathrm{2}} \\ $$$$\mathrm{solve}\:\mathrm{v}:{v}^{\mathrm{2}} −{v}_{\mathrm{0}} ^{\mathrm{2}} =\mathrm{2}{ax} \\ $$
Answered by Rasheed.Sindhi last updated on 26/May/22
1.h=v_0 t+(1/2)gt^2 2v_0 t+gt^2 =2h gt^2 +2v_0 t−2h=0 t=((−2v_0 ±(√((2v_0 )^2 −4(g)(−2h))))/(2g)) =((−2v_0 ±(√(4v_0 ^2 +8gh)))/(2g)) =((−2v_0 ±2(√(v_0 ^2 +2gh)))/(2g)) =((−v_0 ±(√(v_0 ^2 +2gh)))/g) 2.x=v_0 t+(1/2)at^2 Similarly, t=((−v_0 ±(√(v_0 ^2 +2ax)))/a) 3.v^2 −v_0 ^2 =2ax v^2 =v_0 ^2 +2ax v=±(√(v_0 ^2 +2ax))
$$\mathrm{1}.\mathrm{h}=\mathrm{v}_{\mathrm{0}} \mathrm{t}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{gt}^{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{2v}_{\mathrm{0}} \mathrm{t}+\mathrm{gt}^{\mathrm{2}} =\mathrm{2h} \\ $$$$\:\:\:\:\mathrm{gt}^{\mathrm{2}} +\mathrm{2v}_{\mathrm{0}} \mathrm{t}−\mathrm{2h}=\mathrm{0} \\ $$$$\:\:\:\mathrm{t}=\frac{−\mathrm{2v}_{\mathrm{0}} \pm\sqrt{\left(\mathrm{2v}_{\mathrm{0}} \right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{g}\right)\left(−\mathrm{2h}\right)}}{\mathrm{2g}} \\ $$$$\:\:\:\:\:=\frac{−\mathrm{2v}_{\mathrm{0}} \pm\sqrt{\mathrm{4v}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{8gh}}}{\mathrm{2g}} \\ $$$$\:\:\:\:\:=\frac{−\mathrm{2v}_{\mathrm{0}} \pm\mathrm{2}\sqrt{\mathrm{v}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2gh}}}{\mathrm{2g}} \\ $$$$\:\:\:\:\:=\frac{−\mathrm{v}_{\mathrm{0}} \pm\sqrt{\mathrm{v}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2gh}}}{\mathrm{g}} \\ $$$$\mathrm{2}.\mathrm{x}=\mathrm{v}_{\mathrm{0}} \mathrm{t}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{at}^{\mathrm{2}} \\ $$$$\mathrm{Similarly}, \\ $$$$\:\:\:\:\mathrm{t}=\frac{−\mathrm{v}_{\mathrm{0}} \pm\sqrt{\mathrm{v}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2ax}}}{\mathrm{a}} \\ $$$$\mathrm{3}.{v}^{\mathrm{2}} −{v}_{\mathrm{0}} ^{\mathrm{2}} =\mathrm{2}{ax} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{v}^{\mathrm{2}} ={v}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2}{ax} \\ $$$$\:\:\:\:\:\:\:\:\:\:{v}=\pm\sqrt{{v}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2}{ax}} \\ $$$$\:\:\:\: \\ $$
Commented by peter frank last updated on 26/May/22
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *