Question Number 41984 by Tawa1 last updated on 16/Aug/18

$$\mathrm{solve}\:\mathrm{simultaneously}:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\sqrt{\mathrm{k}}\:\:+\:\mathrm{h}\:=\:\mathrm{9}\:\:\:…….\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{k}\:+\:\mathrm{2}\sqrt{\mathrm{h}}\:\:=\:\mathrm{3}\:\:…….\:\left(\mathrm{ii}\right) \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 16/Aug/18

$${x}+\mathrm{2}\sqrt{{y}}\:−\mathrm{9}=\mathrm{0} \\ $$$$\mathrm{2}\sqrt{{x}}\:+{y}−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{2}\sqrt{{y}}\:=\left(\mathrm{9}−{x}\right) \\ $$$$\mathrm{4}{y}=\left(\mathrm{9}−{x}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{9}−{x}\right)^{\mathrm{2}} =\mathrm{4}×\mathrm{1}×{y} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 16/Aug/18

$${this}\:{is}\:{a}\:{parabola}\:{eqn}\: \\ $$$$\mathrm{2}\sqrt{{x}}\:=\left({y}−\mathrm{3}\right) \\ $$$$\mathrm{4}{x}=\left({y}−\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\left({y}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{4}{x} \\ $$$${this}\:{is}\:{also}\:{a}\:{parabola} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 16/Aug/18
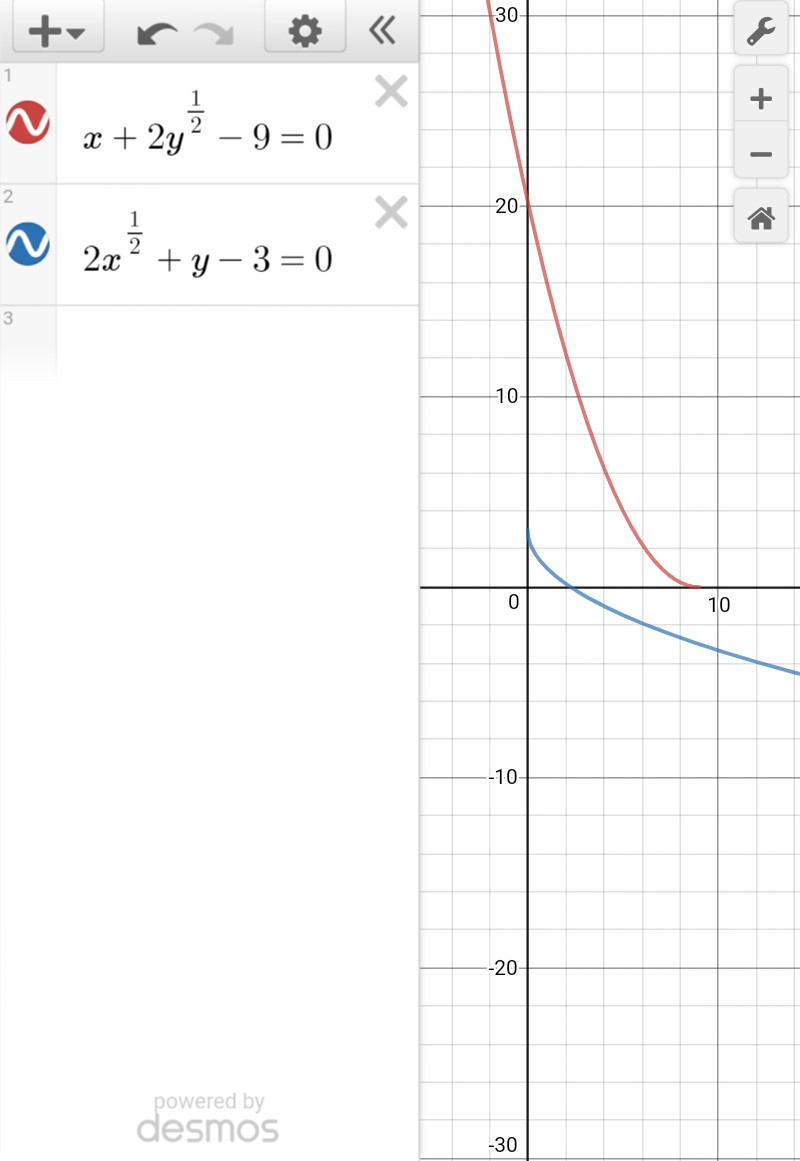
Commented by tanmay.chaudhury50@gmail.com last updated on 16/Aug/18

$${no}\:{solution}… \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 16/Aug/18

Commented by tanmay.chaudhury50@gmail.com last updated on 16/Aug/18

$${if}\:{converted}\:{to}\:{parabola}\:{by}\:{squaring}…{then}\:{solution} \\ $$$${x}=\mathrm{3}.\mathrm{8}\left({approx}\right)\:\:\:{y}=\mathrm{7}.\mathrm{5}\:{approx} \\ $$$${h}=\mathrm{3}.\mathrm{8}\:\:\:\:{k}=\mathrm{7}.\mathrm{5}\:\:\: \\ $$
Commented by MJS last updated on 16/Aug/18
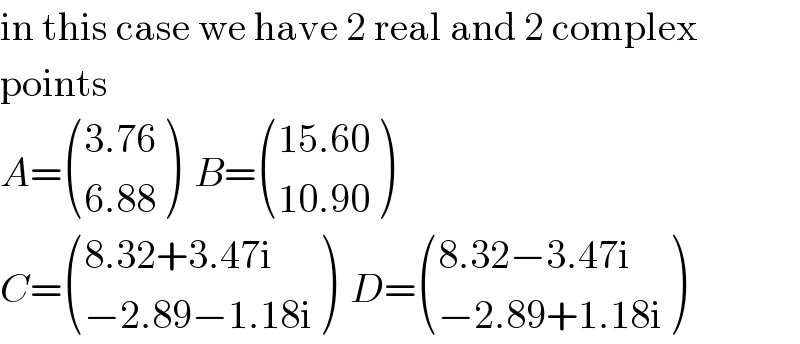
$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{we}\:\mathrm{have}\:\mathrm{2}\:\mathrm{real}\:\mathrm{and}\:\mathrm{2}\:\mathrm{complex} \\ $$$$\mathrm{points} \\ $$$${A}=\begin{pmatrix}{\mathrm{3}.\mathrm{76}}\\{\mathrm{6}.\mathrm{88}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{\mathrm{15}.\mathrm{60}}\\{\mathrm{10}.\mathrm{90}}\end{pmatrix} \\ $$$${C}=\begin{pmatrix}{\mathrm{8}.\mathrm{32}+\mathrm{3}.\mathrm{47i}}\\{−\mathrm{2}.\mathrm{89}−\mathrm{1}.\mathrm{18i}}\end{pmatrix}\:\:{D}=\begin{pmatrix}{\mathrm{8}.\mathrm{32}−\mathrm{3}.\mathrm{47i}}\\{−\mathrm{2}.\mathrm{89}+\mathrm{1}.\mathrm{18i}}\end{pmatrix} \\ $$
Answered by MJS last updated on 16/Aug/18

$$\left({i}\right) \\ $$$$\sqrt{{k}}=\frac{\mathrm{9}−{h}}{\mathrm{2}}\:\Rightarrow\:\mathrm{9}−{h}\geqslant\mathrm{0}\:\Leftrightarrow\:{h}\leqslant\mathrm{9} \\ $$$${k}=\frac{\left(\mathrm{9}−{h}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\left({ii}\right) \\ $$$${k}=\mathrm{3}−\mathrm{2}\sqrt{{h}}\:\Rightarrow\:{h}\geqslant\mathrm{0} \\ $$$$ \\ $$$${k}=\frac{\left(\mathrm{9}−{h}\right)^{\mathrm{2}} }{\mathrm{4}}\:\wedge\:\mathrm{0}\leqslant{h}\leqslant\mathrm{9}\:\Rightarrow\:\mathrm{0}\leqslant{k}\leqslant\frac{\mathrm{81}}{\mathrm{4}} \\ $$$${k}=\mathrm{3}−\mathrm{2}\sqrt{{h}}\:\wedge\:\mathrm{0}\leqslant{h}\leqslant\mathrm{9}\:\Rightarrow\:−\mathrm{3}\leqslant{h}\leqslant\mathrm{3} \\ $$$$\Rightarrow\:\mathrm{0}\leqslant{k}\leqslant\mathrm{3} \\ $$$$\left({i}\right) \\ $$$${h}=\mathrm{9}−\mathrm{2}\sqrt{{k}}\:\wedge\:\mathrm{0}\leqslant{k}\leqslant\mathrm{3}\:\Rightarrow\:\left(\mathrm{9}−\mathrm{2}\sqrt{\mathrm{3}}\right)\leqslant{h}\leqslant\mathrm{9} \\ $$$$\left({ii}\right) \\ $$$$\sqrt{{h}}=\frac{\mathrm{3}−{k}}{\mathrm{2}}\:\Rightarrow\:\mathrm{3}−{k}\geqslant\mathrm{0}\:\Leftrightarrow\:{k}\leqslant\mathrm{3} \\ $$$${h}=\frac{\left(\mathrm{3}−{k}\right)^{\mathrm{2}} }{\mathrm{4}}\:\wedge\:\mathrm{0}\leqslant{k}\leqslant\mathrm{3}\:\Rightarrow\:\mathrm{0}\leqslant{h}\leqslant\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{have}\:\mathrm{2}\:\mathrm{musts}: \\ $$$$\left(\mathrm{9}−\mathrm{2}\sqrt{\mathrm{3}}\right)\leqslant{h}\leqslant\mathrm{9}\:\mathrm{and}\:\mathrm{0}\leqslant{h}\leqslant\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\mathrm{9}−\mathrm{2}\sqrt{\mathrm{3}}\approx\mathrm{5}.\mathrm{54} \\ $$$$\frac{\mathrm{9}}{\mathrm{4}}=\mathrm{2}.\mathrm{25} \\ $$$${h}\geqslant\mathrm{5}.\mathrm{54}\:\mathrm{and}\:{h}\leqslant\mathrm{2}.\mathrm{25}\:\mathrm{is}\:\mathrm{impossible}\:\Rightarrow\:\mathrm{no}\:\mathrm{real} \\ $$$$\mathrm{solution} \\ $$
Commented by Tawa1 last updated on 16/Aug/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{am}\:\mathrm{still}\:\mathrm{expecting}\:\mathrm{the}\:\mathrm{polynomial}\:\mathrm{equation}\:\mathrm{sir}. \\ $$$$\mathrm{any}\:\mathrm{time} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Aug/18

$$\sqrt{{k}}\:=\frac{\mathrm{9}−{h}}{\mathrm{2}} \\ $$$${k}=\frac{\mathrm{81}−\mathrm{18}{h}+{h}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\sqrt{{h}}\:=\frac{\mathrm{3}−{k}}{\mathrm{2}} \\ $$$${h}=\frac{\mathrm{9}−\mathrm{6}{k}+{k}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${so}\:{k}=\frac{\mathrm{81}−\mathrm{18}\left(\frac{\mathrm{9}−\mathrm{6}{k}+{k}^{\mathrm{2}} }{\mathrm{4}}\right)+\frac{\mathrm{81}+\mathrm{36}{k}^{\mathrm{2}} +{k}^{\mathrm{4}} −\mathrm{108}{k}−\mathrm{12}{k}^{\mathrm{3}} +\mathrm{18}{k}^{\mathrm{2}} }{\mathrm{16}}}{\mathrm{4}} \\ $$$$\mathrm{4}{k}=\mathrm{81}×\mathrm{16}−\mathrm{18}×\mathrm{4}\left(\mathrm{9}−\mathrm{6}{k}+{k}^{\mathrm{2}} \right)+\mathrm{81}−\mathrm{108}{k}+\mathrm{54}{k}^{\mathrm{2}} −\mathrm{12}{k}^{\mathrm{3}} +{k}^{\mathrm{4}} \\ $$$$\mathrm{4}{k}=\mathrm{1296}−\mathrm{18}×\mathrm{4}×\mathrm{9}+\mathrm{18}×\mathrm{4}×\mathrm{6}{k}−\mathrm{18}×\mathrm{4}{k}^{\mathrm{2}} −\mathrm{108}{k}+\mathrm{54}{k}^{\mathrm{2}} −\mathrm{12}{k}^{\mathrm{3}} +{k}^{\mathrm{4}} \\ $$$${k}^{\mathrm{4}} −\mathrm{12}{k}^{\mathrm{3}} +{k}^{\mathrm{2}} \left(\mathrm{54}−\mathrm{72}\right)+{k}\left(−\mathrm{108}+\mathrm{18}×\mathrm{4}×\mathrm{6}−\mathrm{4}\right)+\mathrm{1296}−\mathrm{18}×\mathrm{4}×\mathrm{9}=\mathrm{0} \\ $$$${k}^{\mathrm{4}} −\mathrm{12}{k}^{\mathrm{3}} −\mathrm{18}{k}^{\mathrm{2}} +{k}\left(−\mathrm{108}+\mathrm{432}−\mathrm{4}\right)+\mathrm{1296}−\mathrm{648}=\mathrm{0} \\ $$$${k}^{\mathrm{4}} −\mathrm{12}{k}^{\mathrm{3}} −\mathrm{18}{k}^{\mathrm{2}} +\mathrm{320}{k}+\mathrm{648}=\mathrm{0} \\ $$
Commented by MJS last updated on 10/Sep/18

$$\mathrm{typo}\:\mathrm{somewhere}.\:\mathrm{it}\:\mathrm{must}\:\mathrm{be} \\ $$$${k}^{\mathrm{4}} −\mathrm{12}{k}^{\mathrm{3}} −\mathrm{18}{k}^{\mathrm{2}} +\mathrm{260}{k}+\mathrm{729}=\mathrm{0} \\ $$$${k}_{\mathrm{1}} =\mathrm{6}.\mathrm{87588}… \\ $$$${k}_{\mathrm{2}} =\mathrm{10}.\mathrm{9001}… \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{squared}\:\mathrm{2}\:\mathrm{times}\:\mathrm{to}\:\mathrm{get}\:\mathrm{here}\:\mathrm{and}\:\mathrm{both} \\ $$$$\mathrm{resulting}\:\mathrm{pairs}\:\mathrm{of}\:{h},\:{k}\:\mathrm{don}'\mathrm{t}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{given} \\ $$$$\mathrm{equation}\:\mathrm{system} \\ $$
