Question Number 15999 by tawa tawa last updated on 16/Jun/17

$$\mathrm{Solve}\:\mathrm{simultaneously} \\ $$$$\mathrm{2xy}\:=\:\mathrm{x}\:+\:\mathrm{y} \\ $$$$\mathrm{5xz}\:=\:\mathrm{6z}\:−\:\mathrm{2x} \\ $$$$\mathrm{3yz}\:=\:\mathrm{3y}\:+\:\mathrm{4z} \\ $$
Answered by mrW1 last updated on 16/Jun/17
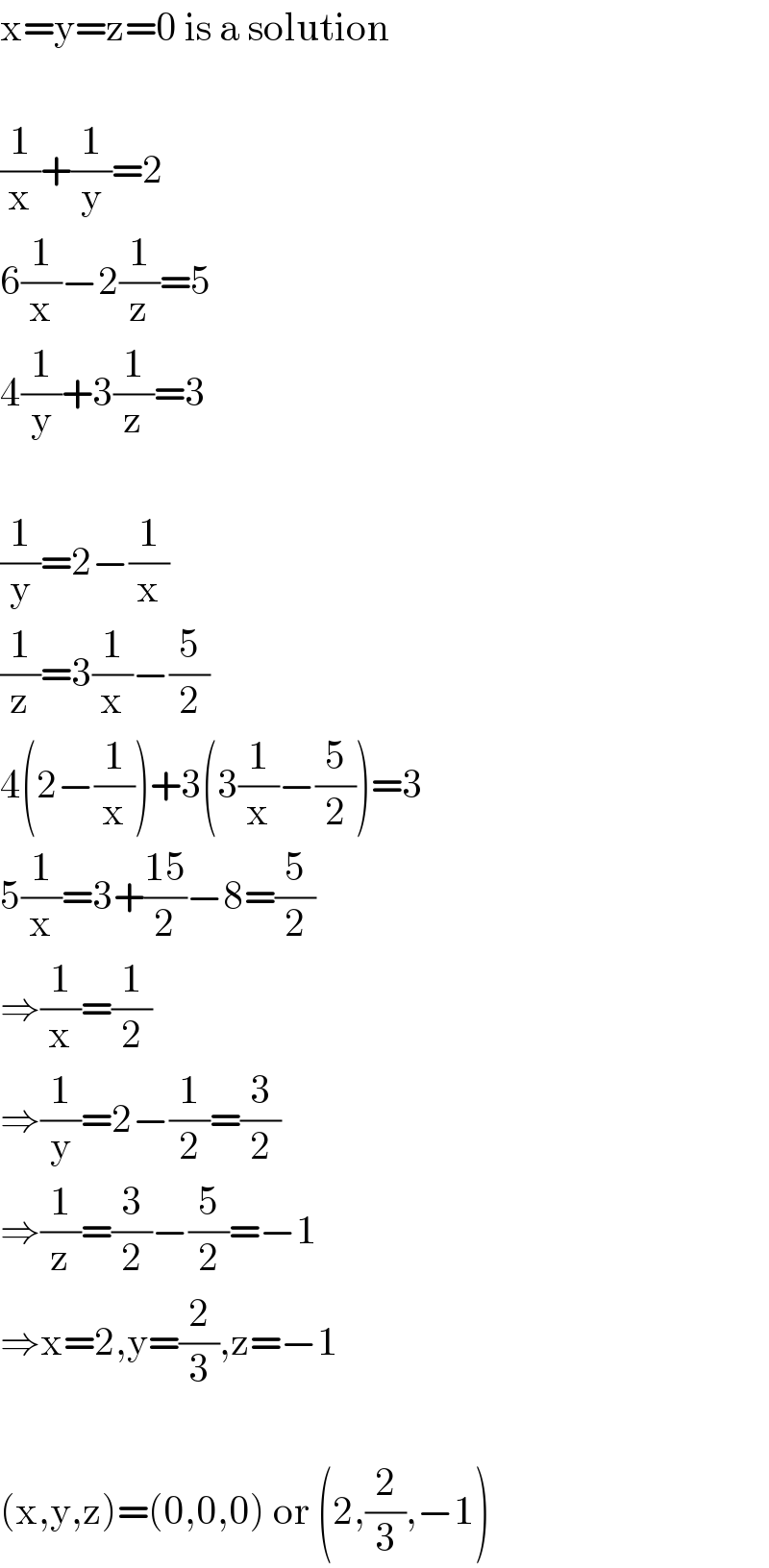
$$\mathrm{x}=\mathrm{y}=\mathrm{z}=\mathrm{0}\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}}=\mathrm{2} \\ $$$$\mathrm{6}\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{2}\frac{\mathrm{1}}{\mathrm{z}}=\mathrm{5} \\ $$$$\mathrm{4}\frac{\mathrm{1}}{\mathrm{y}}+\mathrm{3}\frac{\mathrm{1}}{\mathrm{z}}=\mathrm{3} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{y}}=\mathrm{2}−\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{z}}=\mathrm{3}\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\mathrm{4}\left(\mathrm{2}−\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{3}\left(\mathrm{3}\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{5}}{\mathrm{2}}\right)=\mathrm{3} \\ $$$$\mathrm{5}\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{3}+\frac{\mathrm{15}}{\mathrm{2}}−\mathrm{8}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{x}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{y}}=\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{z}}=\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{5}}{\mathrm{2}}=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{2},\mathrm{y}=\frac{\mathrm{2}}{\mathrm{3}},\mathrm{z}=−\mathrm{1} \\ $$$$ \\ $$$$\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)=\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)\:\mathrm{or}\:\left(\mathrm{2},\frac{\mathrm{2}}{\mathrm{3}},−\mathrm{1}\right) \\ $$
Commented by RasheedSoomro last updated on 16/Jun/17

$$\mathbb{V}\mathcal{NICE}! \\ $$
Commented by tawa tawa last updated on 16/Jun/17

$$\mathrm{i}\:\mathrm{really}\:\mathrm{apprciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
