Question Number 126575 by amns last updated on 22/Dec/20
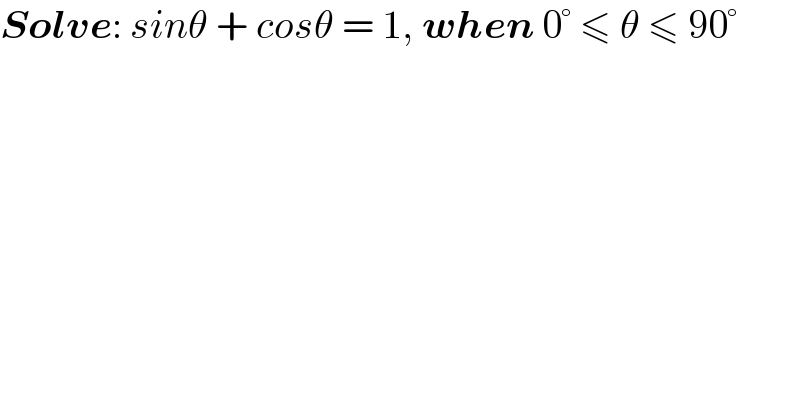
$$\boldsymbol{{Solve}}:\:{sin}\theta\:+\:{cos}\theta\:=\:\mathrm{1},\:\boldsymbol{{when}}\:\mathrm{0}°\:\leqslant\:\theta\:\leqslant\:\mathrm{90}° \\ $$
Commented by amns last updated on 22/Dec/20
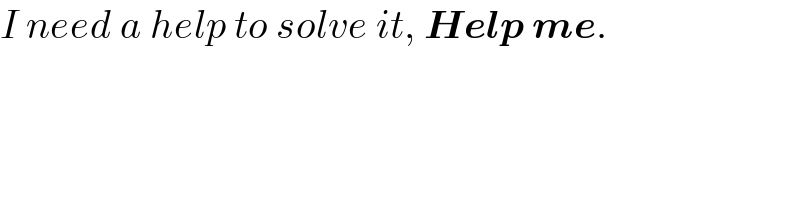
$${I}\:{need}\:{a}\:{help}\:{to}\:{solve}\:{it},\:\boldsymbol{{Help}}\:\boldsymbol{{me}}. \\ $$
Commented by benjo_mathlover last updated on 22/Dec/20

$${wrong}.\: \\ $$
Commented by amns last updated on 22/Dec/20

$${no}…,\:{how}? \\ $$
Commented by amns last updated on 22/Dec/20
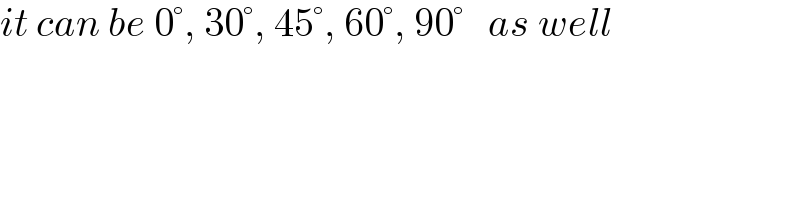
$${it}\:{can}\:{be}\:\mathrm{0}°,\:\mathrm{30}°,\:\mathrm{45}°,\:\mathrm{60}°,\:\mathrm{90}°\:\:\:{as}\:{well} \\ $$
Commented by benjo_mathlover last updated on 22/Dec/20
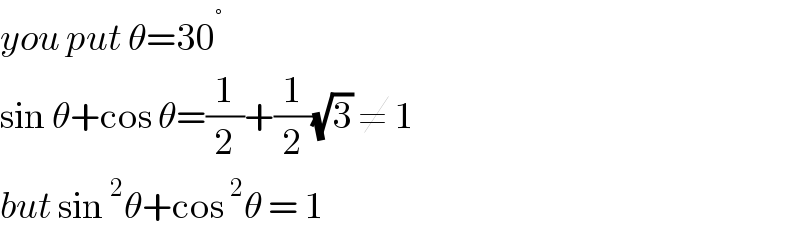
$${you}\:{put}\:\theta=\mathrm{30}^{°} \\ $$$$\mathrm{sin}\:\theta+\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}}\:\neq\:\mathrm{1}\: \\ $$$${but}\:\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{cos}\:^{\mathrm{2}} \theta\:=\:\mathrm{1} \\ $$
Answered by MJS_new last updated on 22/Dec/20
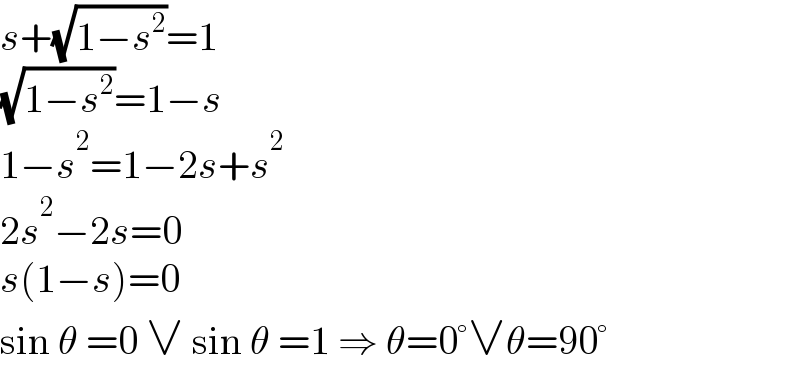
$${s}+\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }=\mathrm{1}−{s} \\ $$$$\mathrm{1}−{s}^{\mathrm{2}} =\mathrm{1}−\mathrm{2}{s}+{s}^{\mathrm{2}} \\ $$$$\mathrm{2}{s}^{\mathrm{2}} −\mathrm{2}{s}=\mathrm{0} \\ $$$${s}\left(\mathrm{1}−{s}\right)=\mathrm{0} \\ $$$$\mathrm{sin}\:\theta\:=\mathrm{0}\:\vee\:\mathrm{sin}\:\theta\:=\mathrm{1}\:\Rightarrow\:\theta=\mathrm{0}°\vee\theta=\mathrm{90}° \\ $$
Answered by amns last updated on 22/Dec/20
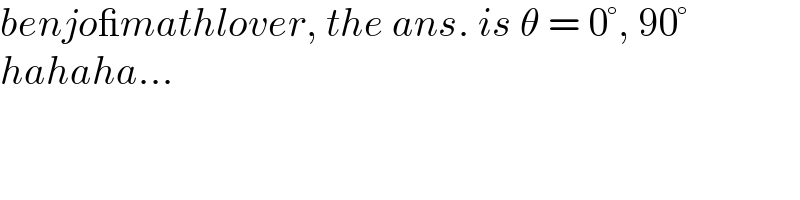
$${benjo\_mathlover},\:{the}\:{ans}.\:{is}\:\theta\:=\:\mathrm{0}°,\:\mathrm{90}° \\ $$$${hahaha}… \\ $$
