Question Number 170371 by cortano1 last updated on 22/May/22

$$\:{solve}\:\frac{\mathrm{sin}\:\left({x}+\mathrm{18}°\right)}{\mathrm{sin}\:{x}}\:=\:\frac{\mathrm{sin}\:\mathrm{18}°}{\mathrm{sin}\:\mathrm{12}°} \\ $$
Answered by greougoury555 last updated on 22/May/22
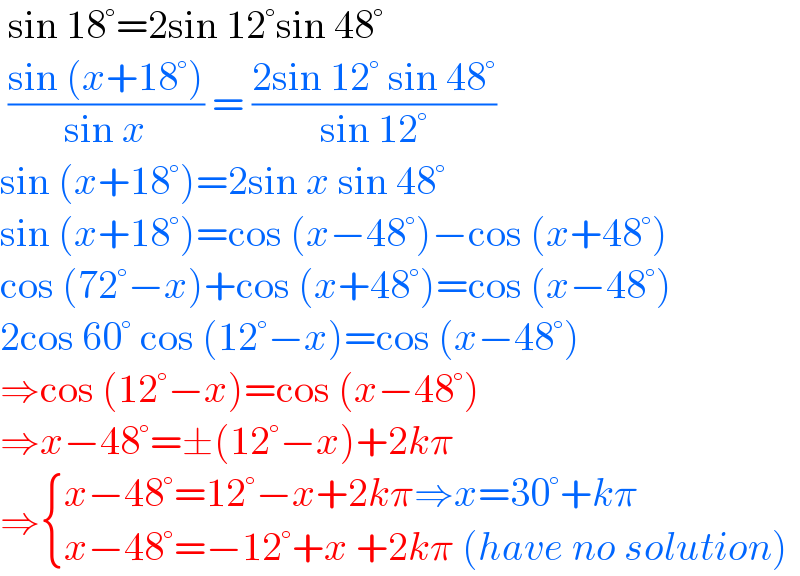
$$\:\mathrm{sin}\:\mathrm{18}°=\mathrm{2sin}\:\mathrm{12}°\mathrm{sin}\:\mathrm{48}° \\ $$$$\:\frac{\mathrm{sin}\:\left({x}+\mathrm{18}°\right)}{\mathrm{sin}\:{x}}\:=\:\frac{\mathrm{2sin}\:\mathrm{12}°\:\mathrm{sin}\:\mathrm{48}°}{\mathrm{sin}\:\mathrm{12}°} \\ $$$$\mathrm{sin}\:\left({x}+\mathrm{18}°\right)=\mathrm{2sin}\:{x}\:\mathrm{sin}\:\mathrm{48}° \\ $$$$\mathrm{sin}\:\left({x}+\mathrm{18}°\right)=\mathrm{cos}\:\left({x}−\mathrm{48}°\right)−\mathrm{cos}\:\left({x}+\mathrm{48}°\right) \\ $$$$\mathrm{cos}\:\left(\mathrm{72}°−{x}\right)+\mathrm{cos}\:\left({x}+\mathrm{48}°\right)=\mathrm{cos}\:\left({x}−\mathrm{48}°\right) \\ $$$$\mathrm{2cos}\:\mathrm{60}°\:\mathrm{cos}\:\left(\mathrm{12}°−{x}\right)=\mathrm{cos}\:\left({x}−\mathrm{48}°\right) \\ $$$$\Rightarrow\mathrm{cos}\:\left(\mathrm{12}°−{x}\right)=\mathrm{cos}\:\left({x}−\mathrm{48}°\right) \\ $$$$\Rightarrow{x}−\mathrm{48}°=\pm\left(\mathrm{12}°−{x}\right)+\mathrm{2}{k}\pi\: \\ $$$$\Rightarrow\begin{cases}{{x}−\mathrm{48}°=\mathrm{12}°−{x}+\mathrm{2}{k}\pi\Rightarrow{x}=\mathrm{30}°+{k}\pi}\\{{x}−\mathrm{48}°=−\mathrm{12}°+{x}\:+\mathrm{2}{k}\pi\:\left({have}\:{no}\:{solution}\right)}\end{cases} \\ $$
