Question Number 170445 by cortano1 last updated on 24/May/22
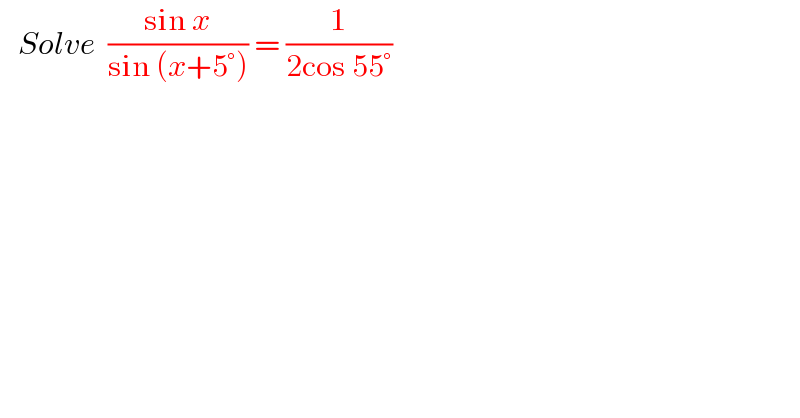
$$\:\:\:{Solve}\:\:\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:\left({x}+\mathrm{5}°\right)}\:=\:\frac{\mathrm{1}}{\mathrm{2cos}\:\mathrm{55}°} \\ $$
Answered by thfchristopher last updated on 24/May/22

$$\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:\left({x}+\mathrm{5}°\right)}=\frac{\mathrm{1}}{\mathrm{2cos}\:\mathrm{55}°} \\ $$$$\Rightarrow\mathrm{2sin}\:{x}\mathrm{cos}\:\mathrm{55}°=\mathrm{sin}\:\left({x}+\mathrm{5}°\right) \\ $$$$\mathrm{cos}\:\mathrm{55}° \\ $$$$=\mathrm{cos}\:\left(\mathrm{60}°−\mathrm{5}°\right) \\ $$$$=\mathrm{cos}\:\mathrm{60}°\mathrm{cos}\:\mathrm{5}°+\mathrm{sin}\:\mathrm{60}°\mathrm{sin}\:\mathrm{5}° \\ $$$$=\frac{\mathrm{cos}\:\mathrm{5}°+\sqrt{\mathrm{3}}\mathrm{sin}\:\mathrm{5}°}{\mathrm{2}} \\ $$$$\therefore\mathrm{2sin}\:{x}\mathrm{cos}\:\mathrm{55}°=\mathrm{sin}\:\left({x}+\mathrm{5}°\right) \\ $$$$\Rightarrow\cancel{\mathrm{sin}\:{x}\mathrm{cos}\:\mathrm{5}°}+\sqrt{\mathrm{3}}\mathrm{sin}\:{x}\cancel{\mathrm{sin}\:\mathrm{5}°}=\cancel{\mathrm{sin}\:{x}\mathrm{cos}\:\mathrm{5}°}+\mathrm{cos}\:{x}\cancel{\mathrm{sin}\:\mathrm{5}°} \\ $$$$\Rightarrow\mathrm{tan}\:{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$${x}=\mathrm{180}{n}+\mathrm{30}°\:\:\:{n}=\mathrm{0},\mathrm{1},\mathrm{2},…. \\ $$
