Question Number 90747 by I want to learn more last updated on 25/Apr/20
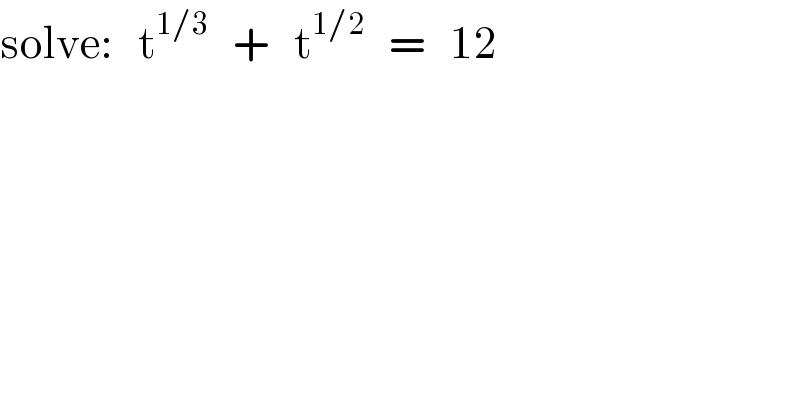
$$\mathrm{solve}:\:\:\:\mathrm{t}^{\mathrm{1}/\mathrm{3}} \:\:\:+\:\:\:\mathrm{t}^{\mathrm{1}/\mathrm{2}} \:\:\:=\:\:\:\mathrm{12} \\ $$
Answered by MJS last updated on 25/Apr/20

$${t}=\mathrm{2}^{\mathrm{6}} =\mathrm{64} \\ $$$$\mathrm{no}\:\mathrm{other}\:\mathrm{solution}\:\mathrm{in}\:\mathbb{C} \\ $$
Commented by I want to learn more last updated on 25/Apr/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Commented by I want to learn more last updated on 25/Apr/20
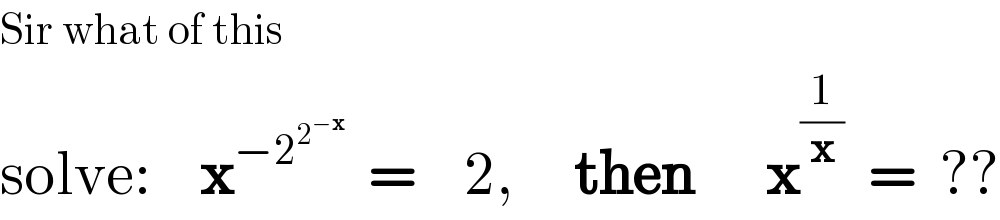
$$\mathrm{Sir}\:\mathrm{what}\:\mathrm{of}\:\mathrm{this} \\ $$$$\mathrm{solve}:\:\:\:\:\boldsymbol{\mathrm{x}}^{−\mathrm{2}^{\mathrm{2}^{−\boldsymbol{\mathrm{x}}} } } \:\:=\:\:\:\:\mathrm{2},\:\:\:\:\:\boldsymbol{\mathrm{then}}\:\:\:\:\:\:\boldsymbol{\mathrm{x}}^{\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}} \:\:=\:\:?? \\ $$
Commented by MJS last updated on 27/Apr/20

$$\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by I want to learn more last updated on 29/Apr/20
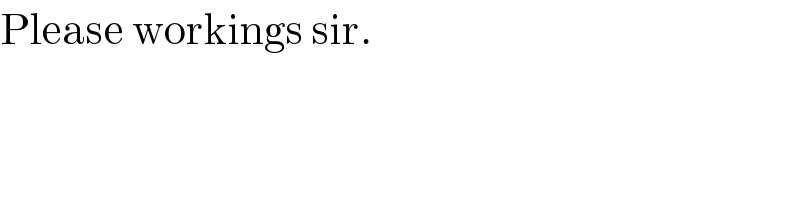
$$\mathrm{Please}\:\mathrm{workings}\:\mathrm{sir}. \\ $$
