Question Number 27393 by kumar123 last updated on 06/Jan/18
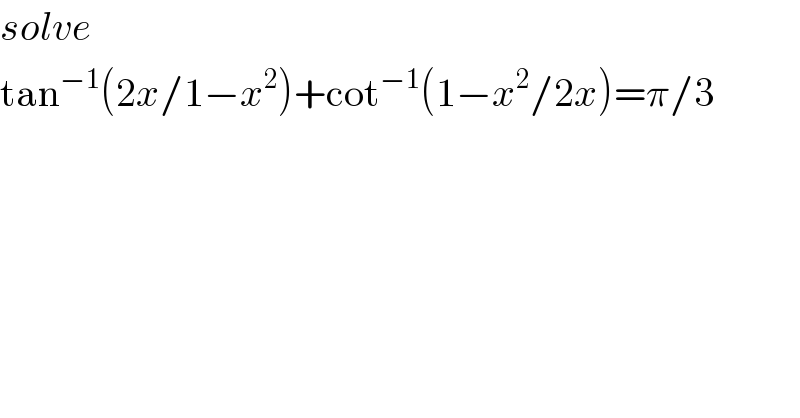
$${solve} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{x}/\mathrm{1}−{x}^{\mathrm{2}} \right)+\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} /\mathrm{2}{x}\right)=\pi/\mathrm{3} \\ $$
Answered by $@ty@m last updated on 06/Jan/18
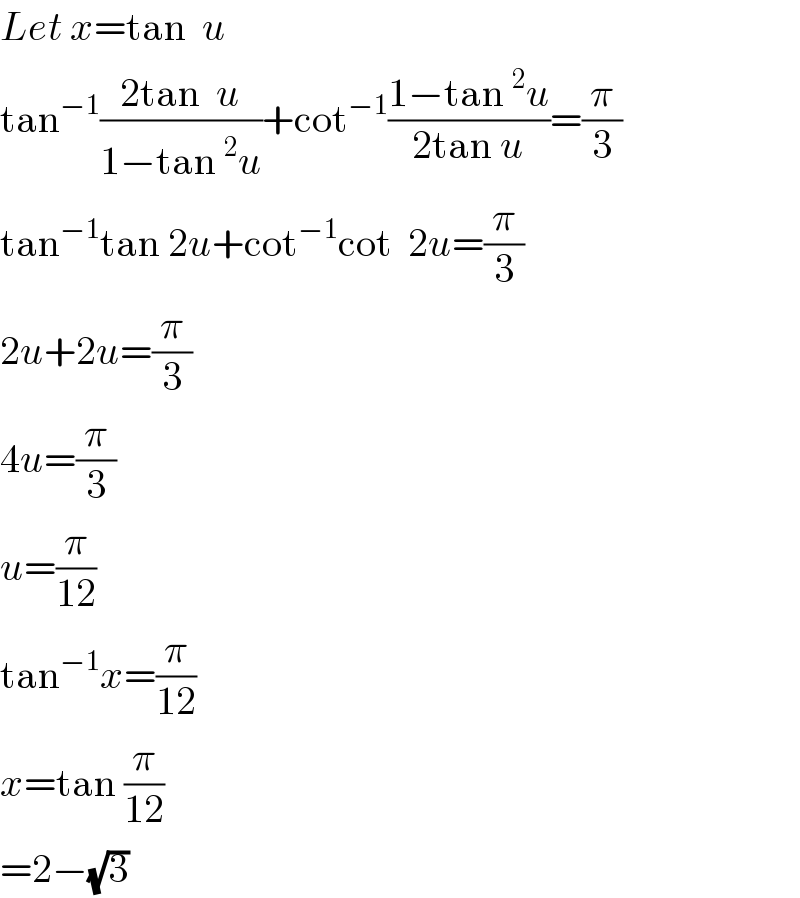
$${Let}\:{x}=\mathrm{tan}\:\:{u} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2tan}\:\:{u}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} {u}}+\mathrm{cot}^{−\mathrm{1}} \frac{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} {u}}{\mathrm{2tan}\:{u}}=\frac{\pi}{\mathrm{3}} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \mathrm{tan}\:\mathrm{2}{u}+\mathrm{cot}^{−\mathrm{1}} \mathrm{cot}\:\:\mathrm{2}{u}=\frac{\pi}{\mathrm{3}} \\ $$$$\mathrm{2}{u}+\mathrm{2}{u}=\frac{\pi}{\mathrm{3}} \\ $$$$\mathrm{4}{u}=\frac{\pi}{\mathrm{3}} \\ $$$${u}=\frac{\pi}{\mathrm{12}} \\ $$$$\mathrm{tan}^{−\mathrm{1}} {x}=\frac{\pi}{\mathrm{12}} \\ $$$${x}=\mathrm{tan}\:\frac{\pi}{\mathrm{12}} \\ $$$$=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$
