Question Number 115121 by bemath last updated on 23/Sep/20
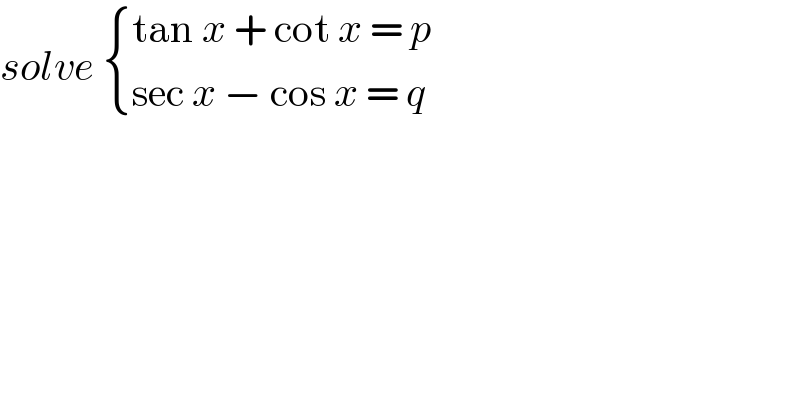
$${solve}\:\begin{cases}{\mathrm{tan}\:{x}\:+\:\mathrm{cot}\:{x}\:=\:{p}}\\{\mathrm{sec}\:{x}\:−\:\mathrm{cos}\:{x}\:=\:{q}}\end{cases} \\ $$
Commented by ATHISHHUZAIN last updated on 23/Sep/20
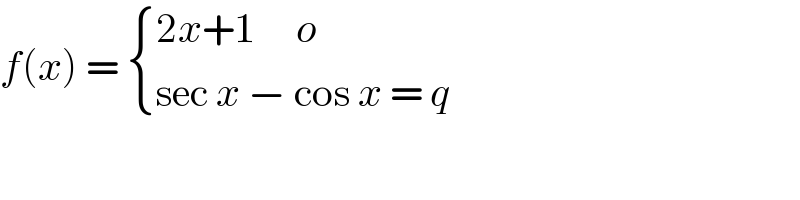
$${f}\left({x}\right)\:=\:\begin{cases}{\mathrm{2}{x}+\mathrm{1}\:\:\:\:\:{o}}\\{\mathrm{sec}\:{x}\:−\:\mathrm{cos}\:{x}\:=\:{q}}\end{cases} \\ $$
Commented by bemath last updated on 23/Sep/20

$$??? \\ $$
Answered by Dwaipayan Shikari last updated on 23/Sep/20
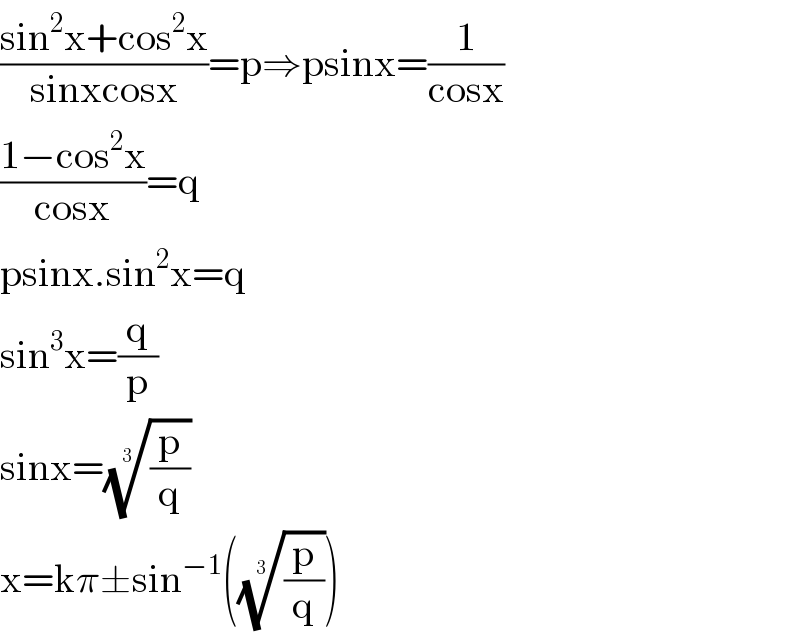
$$\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{sinxcosx}}=\mathrm{p}\Rightarrow\mathrm{psinx}=\frac{\mathrm{1}}{\mathrm{cosx}} \\ $$$$\frac{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{cosx}}=\mathrm{q} \\ $$$$\mathrm{psinx}.\mathrm{sin}^{\mathrm{2}} \mathrm{x}=\mathrm{q} \\ $$$$\mathrm{sin}^{\mathrm{3}} \mathrm{x}=\frac{\mathrm{q}}{\mathrm{p}} \\ $$$$\mathrm{sinx}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{p}}{\mathrm{q}}} \\ $$$$\mathrm{x}=\mathrm{k}\pi\pm\mathrm{sin}^{−\mathrm{1}} \left(\sqrt[{\mathrm{3}}]{\frac{\mathrm{p}}{\mathrm{q}}}\right) \\ $$
