Question Number 80508 by M±th+et£s last updated on 03/Feb/20
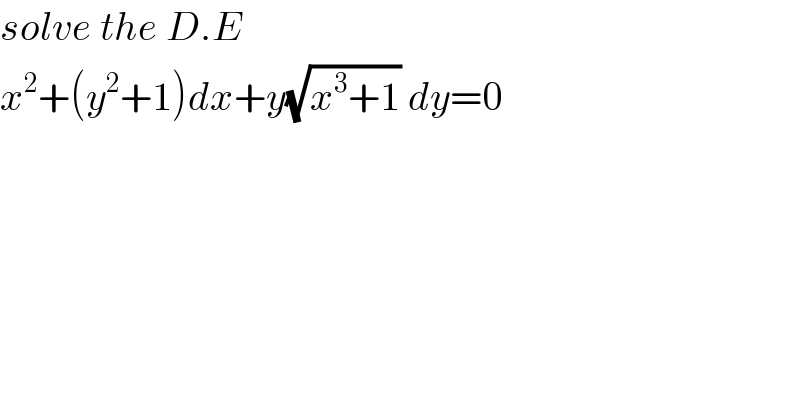
$${solve}\:{the}\:{D}.{E}\: \\ $$$${x}^{\mathrm{2}} +\left({y}^{\mathrm{2}} +\mathrm{1}\right){dx}+{y}\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\:{dy}=\mathrm{0} \\ $$
Commented by mr W last updated on 03/Feb/20

$${syntax}\:{of}\:{equation}\:{is}\:{wrong}. \\ $$
Commented by M±th+et£s last updated on 03/Feb/20

$${so}\:{sorry}\:{but}\:{my}\:{English}\:{isn}^{,} {t}\:{good}\: \\ $$$${and}\:{i}\:{am}\:{trying}\:{to}\:{be}\:{better} \\ $$
Commented by mr W last updated on 03/Feb/20
![your english is no problem sir! but the form of the equation x^2 +(y^2 +1)dx+y(√(x^3 +1)) dy=0 makes no sense. either you have: x^2 +(y^2 +1)+y(√(x^3 +1)) (dy/dx)=0 or you have: [x^2 +(y^2 +1)]dx+y(√(x^3 +1)) dy=0 please recheck!](https://www.tinkutara.com/question/Q80526.png)
$${your}\:{english}\:{is}\:{no}\:{problem}\:{sir}! \\ $$$${but}\:{the}\:{form}\:{of}\:{the}\:{equation}\: \\ $$$${x}^{\mathrm{2}} +\left({y}^{\mathrm{2}} +\mathrm{1}\right){dx}+{y}\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\:{dy}=\mathrm{0} \\ $$$${makes}\:{no}\:{sense}. \\ $$$${either}\:{you}\:{have}: \\ $$$${x}^{\mathrm{2}} +\left({y}^{\mathrm{2}} +\mathrm{1}\right)+{y}\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\:\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$${or}\:{you}\:{have}: \\ $$$$\left[{x}^{\mathrm{2}} +\left({y}^{\mathrm{2}} +\mathrm{1}\right)\right]{dx}+{y}\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\:{dy}=\mathrm{0} \\ $$$$ \\ $$$${please}\:{recheck}! \\ $$
Commented by M±th+et£s last updated on 04/Feb/20

$${you}\:{are}\:{right}\:{sir}\:{its}\:{my}\:{fault}\:{i}\:{forgat} \\ $$$${the}\:{parentheses} \\ $$
