Question Number 170116 by ali009 last updated on 16/May/22
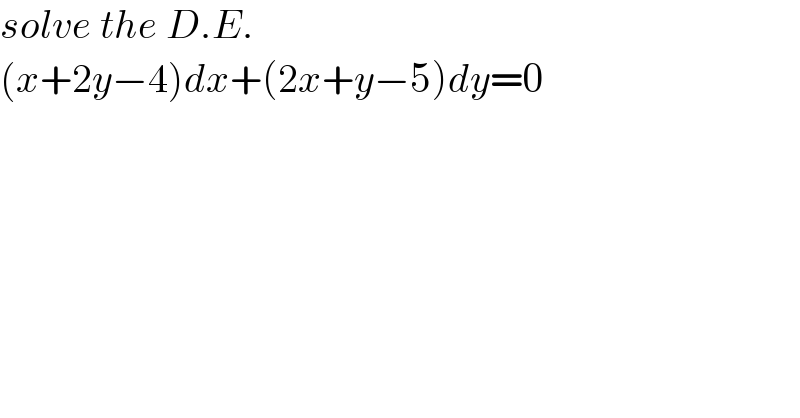
$${solve}\:{the}\:{D}.{E}. \\ $$$$\left({x}+\mathrm{2}{y}−\mathrm{4}\right){dx}+\left(\mathrm{2}{x}+{y}−\mathrm{5}\right){dy}=\mathrm{0} \\ $$
Commented by mr W last updated on 17/May/22

$${see}\:{Q}\mathrm{169558} \\ $$
Answered by ajfour last updated on 17/May/22
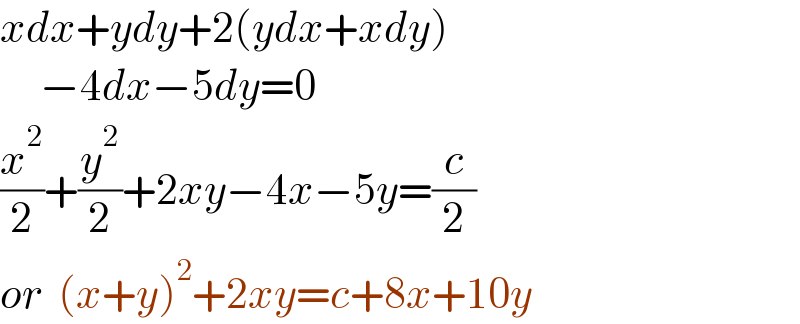
$${xdx}+{ydy}+\mathrm{2}\left({ydx}+{xdy}\right) \\ $$$$\:\:\:\:\:−\mathrm{4}{dx}−\mathrm{5}{dy}=\mathrm{0} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{y}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}{xy}−\mathrm{4}{x}−\mathrm{5}{y}=\frac{{c}}{\mathrm{2}} \\ $$$${or}\:\:\left({x}+{y}\right)^{\mathrm{2}} +\mathrm{2}{xy}={c}+\mathrm{8}{x}+\mathrm{10}{y} \\ $$
