Menu Close

Solve-the-diferential-equatuion-dy-dx-2x-y-1-x-2y-3-

Tinku Tara 0 Comments
Pin




Question Number 37913 by gunawan last updated on 19/Jun/18
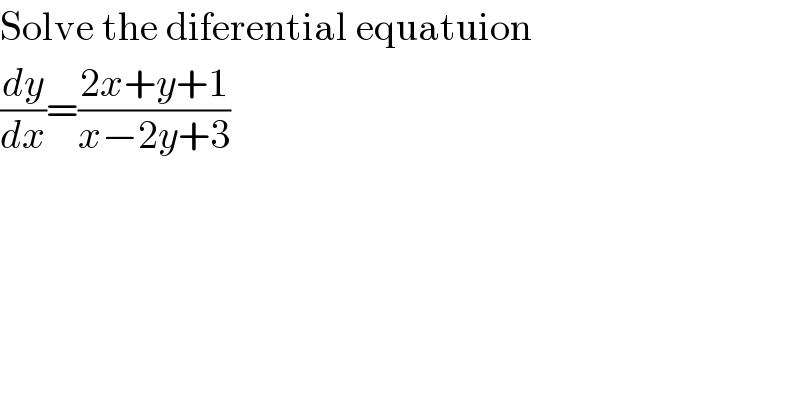
Solve the diferential equatuion (dy/dx)=((2x+y+1)/(x−2y+3))
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{diferential}\:\mathrm{equatuion} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{2}{x}+{y}+\mathrm{1}}{{x}−\mathrm{2}{y}+\mathrm{3}}\: \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Jun/18
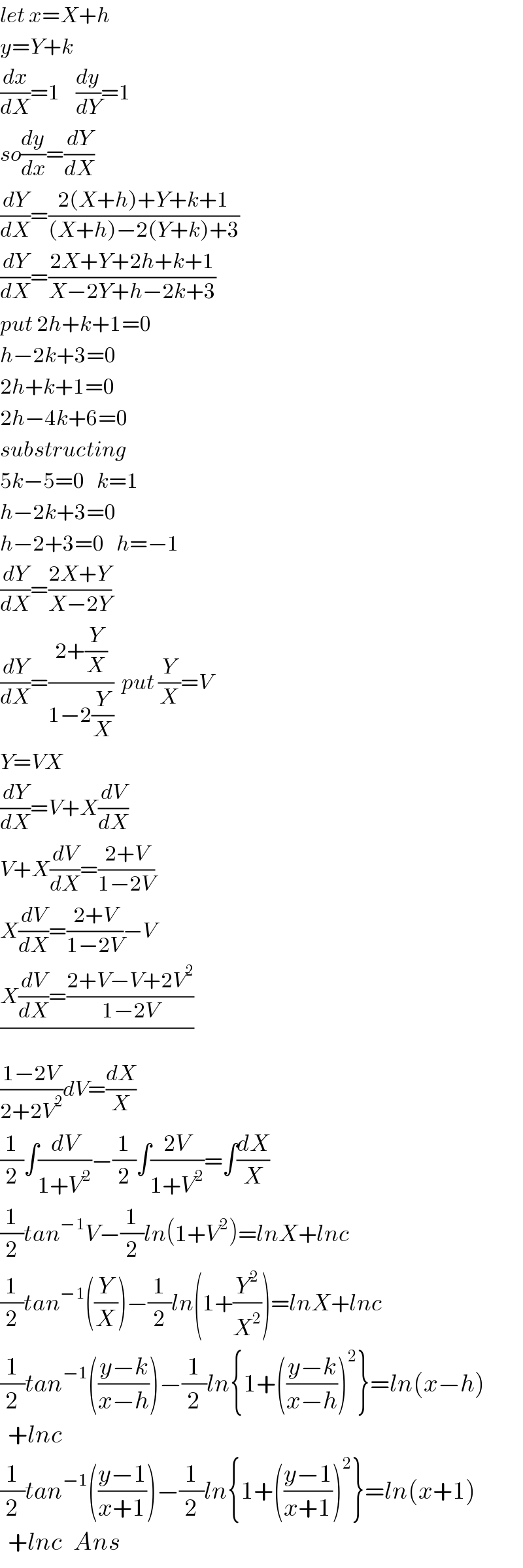
let x=X+h y=Y+k (dx/dX)=1 (dy/dY)=1 so(dy/dx)=(dY/dX) (dY/dX)=((2(X+h)+Y+k+1)/((X+h)−2(Y+k)+3)) (dY/dX)=((2X+Y+2h+k+1)/(X−2Y+h−2k+3)) put 2h+k+1=0 h−2k+3=0 2h+k+1=0 2h−4k+6=0 substructing 5k−5=0 k=1 h−2k+3=0 h−2+3=0 h=−1 (dY/dX)=((2X+Y)/(X−2Y)) (dY/dX)=((2+(Y/X))/(1−2(Y/X))) put (Y/X)=V Y=VX (dY/dX)=V+X(dV/dX) V+X(dV/dX)=((2+V)/(1−2V)) X(dV/dX)=((2+V)/(1−2V))−V ((X(dV/dX)=((2+V−V+2V^2 )/(1−2V)))/) ((1−2V)/(2+2V^2 ))dV=(dX/X) (1/2)∫(dV/(1+V^2 ))−(1/2)∫((2V)/(1+V^2 ))=∫(dX/X) (1/2)tan^(−1) V−(1/2)ln(1+V^2 )=lnX+lnc (1/2)tan^(−1) ((Y/X))−(1/2)ln(1+(Y^2 /X^2 ))=lnX+lnc (1/2)tan^(−1) (((y−k)/(x−h)))−(1/2)ln{1+(((y−k)/(x−h)))^2 }=ln(x−h) +lnc (1/2)tan^(−1) (((y−1)/(x+1)))−(1/2)ln{1+(((y−1)/(x+1)))^2 }=ln(x+1) +lnc Ans
$${let}\:{x}={X}+{h}\:\: \\ $$$${y}={Y}+{k} \\ $$$$\frac{{dx}}{{dX}}=\mathrm{1}\:\:\:\:\frac{{dy}}{{dY}}=\mathrm{1} \\ $$$${so}\frac{{dy}}{{dx}}=\frac{{dY}}{{dX}} \\ $$$$\frac{{dY}}{{dX}}=\frac{\mathrm{2}\left({X}+{h}\right)+{Y}+{k}+\mathrm{1}}{\left({X}+{h}\right)−\mathrm{2}\left({Y}+{k}\right)+\mathrm{3}} \\ $$$$\frac{{dY}}{{dX}}=\frac{\mathrm{2}{X}+{Y}+\mathrm{2}{h}+{k}+\mathrm{1}}{{X}−\mathrm{2}{Y}+{h}−\mathrm{2}{k}+\mathrm{3}} \\ $$$${put}\:\mathrm{2}{h}+{k}+\mathrm{1}=\mathrm{0} \\ $$$${h}−\mathrm{2}{k}+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{2}{h}+{k}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{2}{h}−\mathrm{4}{k}+\mathrm{6}=\mathrm{0} \\ $$$${substructing} \\ $$$$\mathrm{5}{k}−\mathrm{5}=\mathrm{0}\:\:\:{k}=\mathrm{1}\:\: \\ $$$${h}−\mathrm{2}{k}+\mathrm{3}=\mathrm{0} \\ $$$${h}−\mathrm{2}+\mathrm{3}=\mathrm{0}\:\:\:{h}=−\mathrm{1} \\ $$$$\frac{{dY}}{{dX}}=\frac{\mathrm{2}{X}+{Y}}{{X}−\mathrm{2}{Y}} \\ $$$$\frac{{dY}}{{dX}}=\frac{\mathrm{2}+\frac{{Y}}{{X}}}{\mathrm{1}−\mathrm{2}\frac{{Y}}{{X}}}\:\:{put}\:\frac{{Y}}{{X}}={V} \\ $$$${Y}={VX} \\ $$$$\frac{{dY}}{{dX}}={V}+{X}\frac{{dV}}{{dX}} \\ $$$${V}+{X}\frac{{dV}}{{dX}}=\frac{\mathrm{2}+{V}}{\mathrm{1}−\mathrm{2}{V}} \\ $$$${X}\frac{{dV}}{{dX}}=\frac{\mathrm{2}+{V}}{\mathrm{1}−\mathrm{2}{V}}−{V} \\ $$$$\frac{{X}\frac{{dV}}{{dX}}=\frac{\mathrm{2}+{V}−{V}+\mathrm{2}{V}^{\mathrm{2}} }{\mathrm{1}−\mathrm{2}{V}}}{} \\ $$$$\frac{\mathrm{1}−\mathrm{2}{V}}{\mathrm{2}+\mathrm{2}{V}^{\mathrm{2}} }{dV}=\frac{{dX}}{{X}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dV}}{\mathrm{1}+{V}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{V}}{\mathrm{1}+{V}^{\mathrm{2}} }=\int\frac{{dX}}{{X}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} {V}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{V}^{\mathrm{2}} \right)={lnX}+{lnc} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\frac{{Y}}{{X}}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+\frac{{Y}^{\mathrm{2}} }{{X}^{\mathrm{2}} }\right)={lnX}+{lnc} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\frac{{y}−{k}}{{x}−{h}}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left\{\mathrm{1}+\left(\frac{{y}−{k}}{{x}−{h}}\right)^{\mathrm{2}} \right\}={ln}\left({x}−{h}\right) \\ $$$$\:\:+{lnc} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\frac{{y}−\mathrm{1}}{{x}+\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left\{\mathrm{1}+\left(\frac{{y}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{\mathrm{2}} \right\}={ln}\left({x}+\mathrm{1}\right) \\ $$$$\:\:+{lnc}\:\:\:{Ans} \\ $$
Commented by gunawan last updated on 19/Jun/18
Wow, Nice Sir
$$\mathrm{Wow},\:\mathrm{Nice}\:\mathrm{Sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *