Menu Close

solve-the-differencial-equation-1-x-2-y-xy-1-

Tinku Tara 0 Comments
Pin




Question Number 27594 by abdo imad last updated on 10/Jan/18
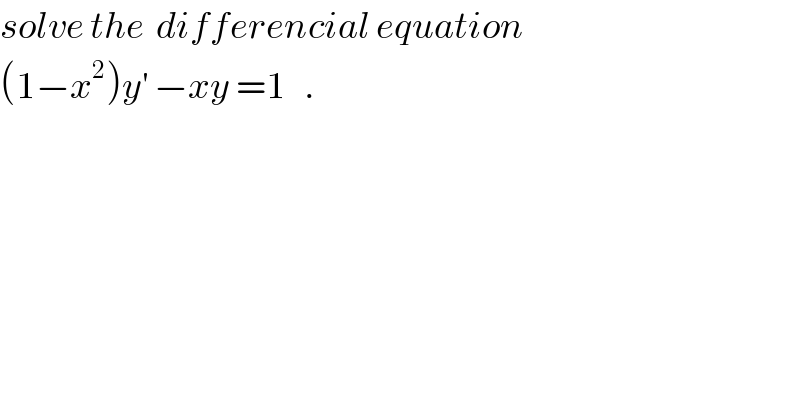
solve the differencial equation (1−x^2 )y^′ −xy =1 .
$${solve}\:{the}\:\:{differencial}\:{equation} \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y}^{'} \:−{xy}\:=\mathrm{1}\:\:\:. \\ $$
Commented by abdo imad last updated on 12/Jan/18
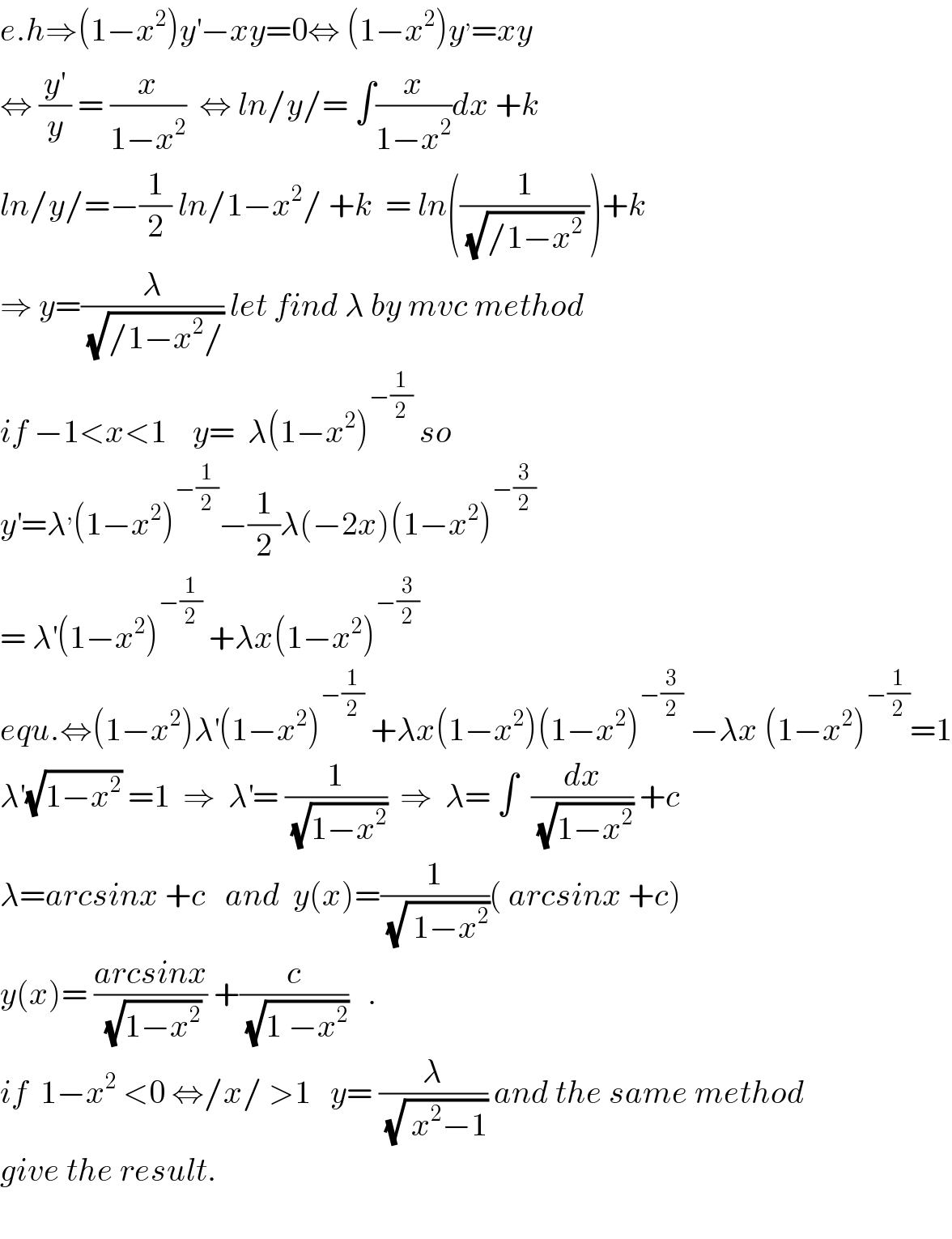
e.h⇒(1−x^2 )y^′ −xy=0⇔ (1−x^2 )y^, =xy ⇔ (y^′ /y) = (x/(1−x^2 )) ⇔ ln/y/= ∫(x/(1−x^2 ))dx +k ln/y/=−(1/2) ln/1−x^2 / +k = ln((1/( (√(/1−x^2 )) )))+k ⇒ y=(λ/( (√(/1−x^2 /)))) let find λ by mvc method if −1<x<1 y= λ(1−x^2 )^(−(1/2)) so y^′ =λ^, (1−x^2 )^(−(1/2)) −(1/2)λ(−2x)(1−x^2 )^(−(3/2)) = λ^′ (1−x^2 )^(−(1/2)) +λx(1−x^2 )^(−(3/2)) equ.⇔(1−x^2 )λ^′ (1−x^2 )^(−(1/2)) +λx(1−x^2 )(1−x^2 )^(−(3/2)) −λx (1−x^2 )^(−(1/2)) =1 λ′(√(1−x^2 )) =1 ⇒ λ^′ = (1/( (√(1−x^2 )))) ⇒ λ= ∫ (dx/( (√(1−x^2 )))) +c λ=arcsinx +c and y(x)=(1/( (√( 1−x^2 ))))( arcsinx +c) y(x)= ((arcsinx)/( (√(1−x^2 )))) +(c/( (√(1 −x^2 )))) . if 1−x^2 <0 ⇔/x/ >1 y= (λ/( (√( x^2 −1)))) and the same method give the result.
$${e}.{h}\Rightarrow\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y}^{'} −{xy}=\mathrm{0}\Leftrightarrow\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y}^{,} ={xy}\: \\ $$$$\Leftrightarrow\:\frac{{y}^{'} }{{y}}\:=\:\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\:\:\Leftrightarrow\:{ln}/{y}/=\:\int\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}\:+{k} \\ $$$${ln}/{y}/=−\frac{\mathrm{1}}{\mathrm{2}}\:{ln}/\mathrm{1}−{x}^{\mathrm{2}} /\:+{k}\:\:=\:{ln}\left(\frac{\mathrm{1}}{\:\sqrt{/\mathrm{1}−{x}^{\mathrm{2}} }\:}\right)+{k} \\ $$$$\Rightarrow\:{y}=\frac{\lambda}{\:\sqrt{/\mathrm{1}−{x}^{\mathrm{2}} /}}\:{let}\:{find}\:\lambda\:{by}\:{mvc}\:{method} \\ $$$${if}\:−\mathrm{1}<{x}<\mathrm{1}\:\:\:\:{y}=\:\:\lambda\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:{so} \\ $$$${y}^{'} =\lambda^{,} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{2}}\lambda\left(−\mathrm{2}{x}\right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$=\:\lambda^{'} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:+\lambda{x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$${equ}.\Leftrightarrow\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\lambda^{'} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:+\lambda{x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:−\lambda{x}\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{1} \\ $$$$\lambda'\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:=\mathrm{1}\:\:\Rightarrow\:\:\lambda^{'} =\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\:\Rightarrow\:\:\lambda=\:\int\:\:\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:+{c} \\ $$$$\lambda={arcsinx}\:+{c}\:\:\:{and}\:\:{y}\left({x}\right)=\frac{\mathrm{1}}{\:\sqrt{\:\mathrm{1}−{x}^{\mathrm{2}} }}\left(\:{arcsinx}\:+{c}\right) \\ $$$${y}\left({x}\right)=\:\frac{{arcsinx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:+\frac{{c}}{\:\sqrt{\mathrm{1}\:−{x}^{\mathrm{2}} }}\:\:\:. \\ $$$${if}\:\:\mathrm{1}−{x}^{\mathrm{2}} \:<\mathrm{0}\:\Leftrightarrow/{x}/\:>\mathrm{1}\:\:\:{y}=\:\frac{\lambda}{\:\sqrt{\:{x}^{\mathrm{2}} −\mathrm{1}}}\:{and}\:{the}\:{same}\:{method}\: \\ $$$${give}\:{the}\:{result}. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *