Menu Close

solve-the-differential-equation-a-d-2-y-dx-2-sin-2-x-y-b-d-2-y-dx-2-cos-x-y-

Tinku Tara 0 Comments
Pin




Question Number 81054 by peter frank last updated on 09/Feb/20
solve the differential equation (a)(d^2 y/dx^2 )=sin^2 (x+y) (b)(d^2 y/dx^2 )=cos (x+y)
$${solve}\:{the}\:{differential} \\ $$$${equation} \\ $$$$\left({a}\right)\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\mathrm{sin}\:^{\mathrm{2}} \left({x}+{y}\right) \\ $$$$\left({b}\right)\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\mathrm{cos}\:\left({x}+{y}\right) \\ $$
Commented by mr W last updated on 14/Feb/20
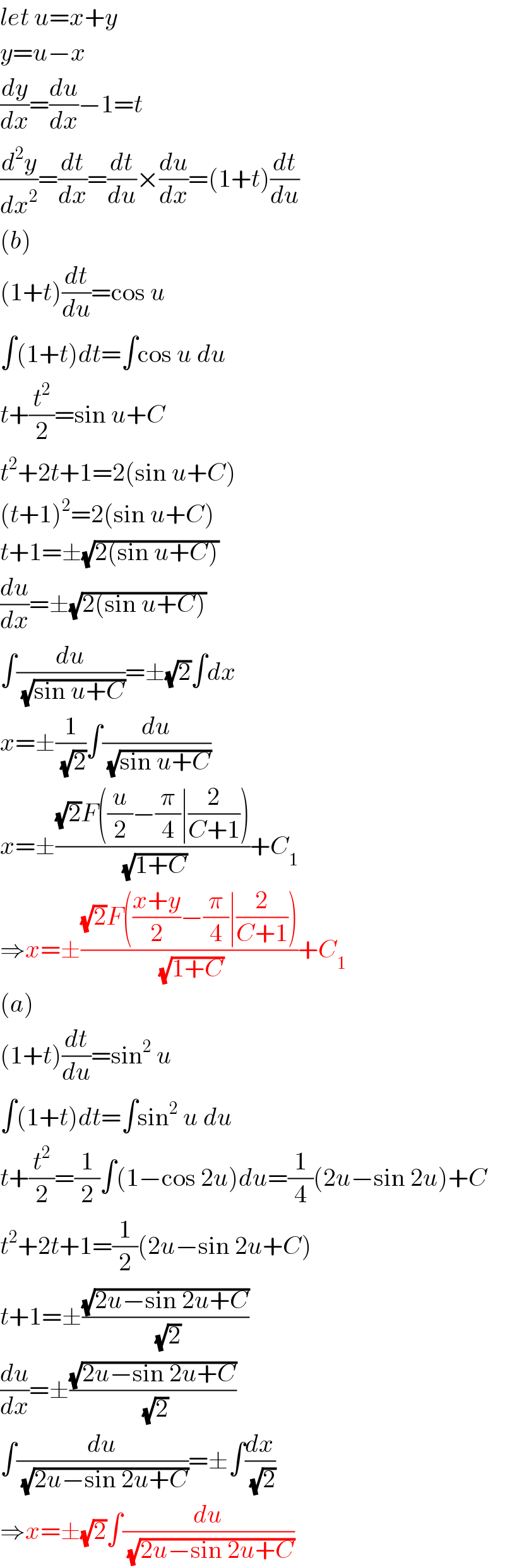
let u=x+y y=u−x (dy/dx)=(du/dx)−1=t (d^2 y/dx^2 )=(dt/dx)=(dt/du)×(du/dx)=(1+t)(dt/du) (b) (1+t)(dt/du)=cos u ∫(1+t)dt=∫cos u du t+(t^2 /2)=sin u+C t^2 +2t+1=2(sin u+C) (t+1)^2 =2(sin u+C) t+1=±(√(2(sin u+C))) (du/dx)=±(√(2(sin u+C))) ∫(du/( (√(sin u+C))))=±(√2)∫dx x=±(1/( (√2)))∫(du/( (√(sin u+C)))) x=±(((√2)F((u/2)−(π/4)∣(2/(C+1))))/( (√(1+C))))+C_1 ⇒x=±(((√2)F(((x+y)/2)−(π/4)∣(2/(C+1))))/( (√(1+C))))+C_1 (a) (1+t)(dt/du)=sin^2 u ∫(1+t)dt=∫sin^2 u du t+(t^2 /2)=(1/2)∫(1−cos 2u)du=(1/4)(2u−sin 2u)+C t^2 +2t+1=(1/2)(2u−sin 2u+C) t+1=±((√(2u−sin 2u+C))/( (√2))) (du/dx)=±((√(2u−sin 2u+C))/( (√2))) ∫(du/( (√(2u−sin 2u+C))))=±∫(dx/( (√2))) ⇒x=±(√2)∫(du/( (√(2u−sin 2u+C))))
$${let}\:{u}={x}+{y} \\ $$$${y}={u}−{x} \\ $$$$\frac{{dy}}{{dx}}=\frac{{du}}{{dx}}−\mathrm{1}={t} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{dt}}{{dx}}=\frac{{dt}}{{du}}×\frac{{du}}{{dx}}=\left(\mathrm{1}+{t}\right)\frac{{dt}}{{du}} \\ $$$$\left({b}\right) \\ $$$$\left(\mathrm{1}+{t}\right)\frac{{dt}}{{du}}=\mathrm{cos}\:{u} \\ $$$$\int\left(\mathrm{1}+{t}\right){dt}=\int\mathrm{cos}\:{u}\:{du} \\ $$$${t}+\frac{{t}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{sin}\:{u}+{C} \\ $$$${t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}=\mathrm{2}\left(\mathrm{sin}\:{u}+{C}\right) \\ $$$$\left({t}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2}\left(\mathrm{sin}\:{u}+{C}\right) \\ $$$${t}+\mathrm{1}=\pm\sqrt{\mathrm{2}\left(\mathrm{sin}\:{u}+{C}\right)} \\ $$$$\frac{{du}}{{dx}}=\pm\sqrt{\mathrm{2}\left(\mathrm{sin}\:{u}+{C}\right)} \\ $$$$\int\frac{{du}}{\:\sqrt{\mathrm{sin}\:{u}+{C}}}=\pm\sqrt{\mathrm{2}}\int{dx} \\ $$$${x}=\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{du}}{\:\sqrt{\mathrm{sin}\:{u}+{C}}} \\ $$$${x}=\pm\frac{\sqrt{\mathrm{2}}{F}\left(\frac{{u}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\mid\frac{\mathrm{2}}{{C}+\mathrm{1}}\right)}{\:\sqrt{\mathrm{1}+{C}}}+{C}_{\mathrm{1}} \\ $$$$\Rightarrow{x}=\pm\frac{\sqrt{\mathrm{2}}{F}\left(\frac{{x}+{y}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\mid\frac{\mathrm{2}}{{C}+\mathrm{1}}\right)}{\:\sqrt{\mathrm{1}+{C}}}+{C}_{\mathrm{1}} \\ $$$$\left({a}\right) \\ $$$$\left(\mathrm{1}+{t}\right)\frac{{dt}}{{du}}=\mathrm{sin}^{\mathrm{2}} \:{u} \\ $$$$\int\left(\mathrm{1}+{t}\right){dt}=\int\mathrm{sin}^{\mathrm{2}} \:{u}\:{du} \\ $$$${t}+\frac{{t}^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{u}\right){du}=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}{u}−\mathrm{sin}\:\mathrm{2}{u}\right)+{C} \\ $$$${t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{u}−\mathrm{sin}\:\mathrm{2}{u}+{C}\right) \\ $$$${t}+\mathrm{1}=\pm\frac{\sqrt{\mathrm{2}{u}−\mathrm{sin}\:\mathrm{2}{u}+{C}}}{\:\sqrt{\mathrm{2}}} \\ $$$$\frac{{du}}{{dx}}=\pm\frac{\sqrt{\mathrm{2}{u}−\mathrm{sin}\:\mathrm{2}{u}+{C}}}{\:\sqrt{\mathrm{2}}} \\ $$$$\int\frac{{du}}{\:\sqrt{\mathrm{2}{u}−\mathrm{sin}\:\mathrm{2}{u}+{C}}}=\pm\int\frac{{dx}}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow{x}=\pm\sqrt{\mathrm{2}}\int\frac{{du}}{\:\sqrt{\mathrm{2}{u}−\mathrm{sin}\:\mathrm{2}{u}+{C}}} \\ $$
Commented by peter frank last updated on 14/Feb/20
thank you
$${thank}\:{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *