Menu Close

Solve-the-differential-equation-a-x-x-y-dy-dx-x-2-xy-3y-2-b-y-xy-2-x-dy-dx-0-c-x-2-d-2-y-dx-2-2x-dy-dx-2-2x-2-1-y-24x-3-given-that-dy-dx-6-d-2-y-dx-2-0-

Tinku Tara 0 Comments
Pin




Question Number 50140 by peter frank last updated on 14/Dec/18
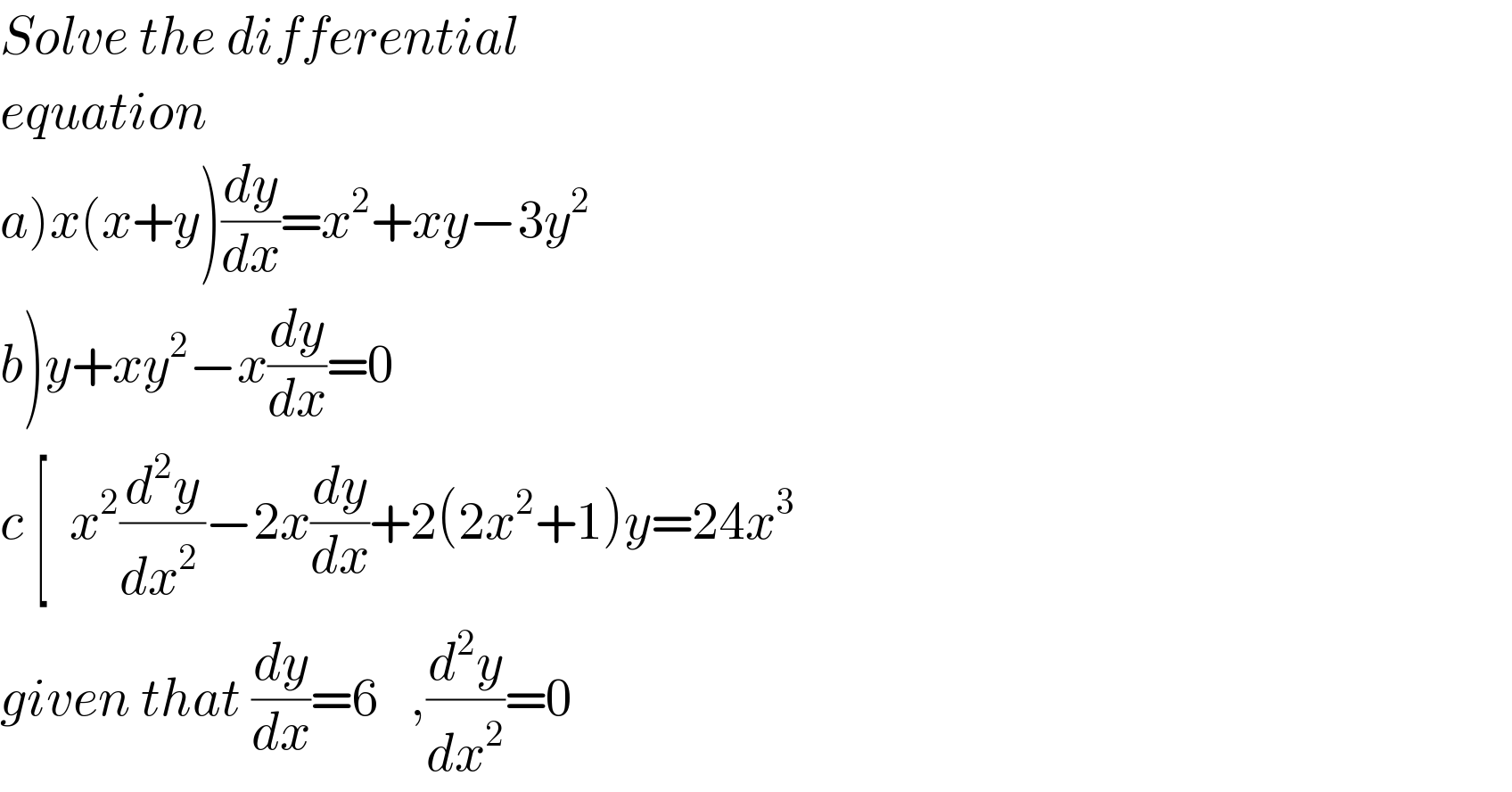
Solve the differential equation a)x(x+y)(dy/dx)=x^2 +xy−3y^2 b)y+xy^2 −x(dy/dx)=0 c [ x^2 (d^2 y/dx^(2 ) )−2x(dy/dx)+2(2x^2 +1)y=24x^3 given that (dy/dx)=6 ,(d^2 y/dx^2 )=0
$${Solve}\:{the}\:{differential} \\ $$$${equation} \\ $$$$\left.{a}\right){x}\left({x}+{y}\right)\frac{{dy}}{{dx}}={x}^{\mathrm{2}} +{xy}−\mathrm{3}{y}^{\mathrm{2}} \\ $$$$\left.{b}\right){y}+{xy}^{\mathrm{2}} −{x}\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$${c}\:\left[\:\:{x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}\:} }−\mathrm{2}{x}\frac{{dy}}{{dx}}+\mathrm{2}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right){y}=\mathrm{24}{x}^{\mathrm{3}} \right. \\ $$$${given}\:{that}\:\frac{{dy}}{{dx}}=\mathrm{6}\:\:\:,\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\mathrm{0} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Dec/18
a)(dy/dx)=((x^2 +xy−3y^2 )/(x^2 +xy))=((1+(y/x)−((3y^2 )/x^2 ))/(1+(y/x))) [deviding N_r and D_r by x^2 ] (y/x)=t y=tx so (dy/dx)=t+x(dt/dx) t+x(dt/dx)=((1+t−3t^2 )/(1+t)) x(dt/dx)=((1+t−3t^2 )/(1+t))−t x(dt/dx)=((1+t−3t^2 −t−t^2 )/(1+t)) ((1+t)/(1−4t^2 ))dt=(dx/x) (1/4)∫((1+t)/((1/4)−t^2 ))dt=∫(dx/x) (1/4)∫(dt/(((1/2))^2 −t^2 ))+(1/4)×((−1)/2)∫((d((1/4)−t^2 ))/((1/4)−t^2 ))=∫(dx/x) (1/4)∫(dt/(((1/2))^2 −t^2 ))−(1/8)∫((d((1/4)−t^2 ))/((1/4)−t^2 ))=∫(dx/x) (1/4)×(1/(2×(1/2)))ln((((1/2)+t)/((1/2)−t)))−(1/8)ln((1/4)−t^2 )=lnx+lnc (1/4)ln(((1+2t)/(1−2t)))−(1/8)ln((1/4)−t^2 )=lnx+lnc (1/4)ln(((1+((2y)/x))/(1−((2y)/x))))−(1/8)ln((1/4)−(y^2 /x^2 ))=lnx+lnc ln{(((x+2y)/(x−2y)))}^(1/4) −ln(((x^2 −4y^2 )/(4x^2 )))^(1/8) =ln(xc) (((x+2y)/(x−2y)))^(1/4) ×(((4x^2 )/(x^2 −4y^2 )))^(1/8) =xc (x+2y)^((1/4)−(1/8)) ×(1/((x−2y)^((1/4)+(1/8)) ))×(4x^2 )^(1/8) =xc (x+2y)^(1/8) ×(1/((x−2y)^(3/8) ))×(4x^2 )^(1/8) =xc
$$\left.{a}\right)\frac{{dy}}{{dx}}=\frac{{x}^{\mathrm{2}} +{xy}−\mathrm{3}{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{xy}}=\frac{\mathrm{1}+\frac{{y}}{{x}}−\frac{\mathrm{3}{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }}{\mathrm{1}+\frac{{y}}{{x}}}\:\:\left[{deviding}\:{N}_{{r}} {and}\:{D}_{{r}} \:{by}\:{x}^{\mathrm{2}} \right] \\ $$$$\frac{{y}}{{x}}={t}\:\:\:\:{y}={tx}\:\:{so}\:\:\frac{{dy}}{{dx}}={t}+{x}\frac{{dt}}{{dx}} \\ $$$${t}+{x}\frac{{dt}}{{dx}}=\frac{\mathrm{1}+{t}−\mathrm{3}{t}^{\mathrm{2}} }{\mathrm{1}+{t}} \\ $$$${x}\frac{{dt}}{{dx}}=\frac{\mathrm{1}+{t}−\mathrm{3}{t}^{\mathrm{2}} }{\mathrm{1}+{t}}−{t} \\ $$$${x}\frac{{dt}}{{dx}}=\frac{\mathrm{1}+{t}−\mathrm{3}{t}^{\mathrm{2}} −{t}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}} \\ $$$$\frac{\mathrm{1}+{t}}{\mathrm{1}−\mathrm{4}{t}^{\mathrm{2}} }{dt}=\frac{{dx}}{{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{1}+{t}}{\frac{\mathrm{1}}{\mathrm{4}}−{t}^{\mathrm{2}} }{dt}=\int\frac{{dx}}{{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dt}}{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}}×\frac{−\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left(\frac{\mathrm{1}}{\mathrm{4}}−{t}^{\mathrm{2}} \right)}{\frac{\mathrm{1}}{\mathrm{4}}−{t}^{\mathrm{2}} }=\int\frac{{dx}}{{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dt}}{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{8}}\int\frac{{d}\left(\frac{\mathrm{1}}{\mathrm{4}}−{t}^{\mathrm{2}} \right)}{\frac{\mathrm{1}}{\mathrm{4}}−{t}^{\mathrm{2}} }=\int\frac{{dx}}{{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{1}}{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}}{ln}\left(\frac{\frac{\mathrm{1}}{\mathrm{2}}+{t}}{\frac{\mathrm{1}}{\mathrm{2}}−{t}}\right)−\frac{\mathrm{1}}{\mathrm{8}}{ln}\left(\frac{\mathrm{1}}{\mathrm{4}}−{t}^{\mathrm{2}} \right)={lnx}+{lnc} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{\mathrm{1}+\mathrm{2}{t}}{\mathrm{1}−\mathrm{2}{t}}\right)−\frac{\mathrm{1}}{\mathrm{8}}{ln}\left(\frac{\mathrm{1}}{\mathrm{4}}−{t}^{\mathrm{2}} \right)={lnx}+{lnc} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{\mathrm{1}+\frac{\mathrm{2}{y}}{{x}}}{\mathrm{1}−\frac{\mathrm{2}{y}}{{x}}}\right)−\frac{\mathrm{1}}{\mathrm{8}}{ln}\left(\frac{\mathrm{1}}{\mathrm{4}}−\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)={lnx}+{lnc} \\ $$$${ln}\left\{\left(\frac{{x}+\mathrm{2}{y}}{{x}−\mathrm{2}{y}}\right)\right\}^{\frac{\mathrm{1}}{\mathrm{4}}} −{ln}\left(\frac{{x}^{\mathrm{2}} −\mathrm{4}{y}^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{\mathrm{8}}} ={ln}\left({xc}\right) \\ $$$$\left(\frac{{x}+\mathrm{2}{y}}{{x}−\mathrm{2}{y}}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} ×\left(\frac{\mathrm{4}{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −\mathrm{4}{y}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{\mathrm{8}}} ={xc} \\ $$$$\left({x}+\mathrm{2}{y}\right)^{\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{8}}} ×\frac{\mathrm{1}}{\left({x}−\mathrm{2}{y}\right)^{\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}} }×\left(\mathrm{4}{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{8}}} ={xc} \\ $$$$\left({x}+\mathrm{2}{y}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} ×\frac{\mathrm{1}}{\left({x}−\mathrm{2}{y}\right)^{\frac{\mathrm{3}}{\mathrm{8}}} }×\left(\mathrm{4}{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{8}}} ={xc} \\ $$$$ \\ $$
Commented by peter frank last updated on 14/Dec/18
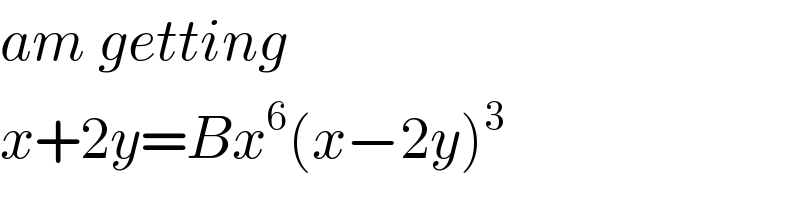
am getting x+2y=Bx^6 (x−2y)^3
$${am}\:{getting}\: \\ $$$${x}+\mathrm{2}{y}={Bx}^{\mathrm{6}} \left({x}−\mathrm{2}{y}\right)^{\mathrm{3}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 14/Dec/18
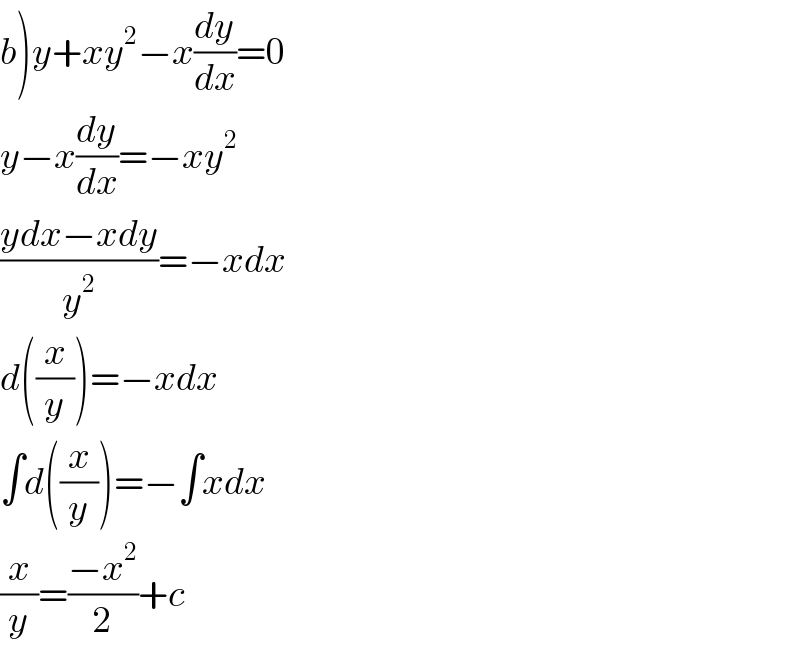
b)y+xy^2 −x(dy/dx)=0 y−x(dy/dx)=−xy^2 ((ydx−xdy)/y^2 )=−xdx d((x/y))=−xdx ∫d((x/y))=−∫xdx (x/y)=((−x^2 )/2)+c
$$\left.{b}\right){y}+{xy}^{\mathrm{2}} −{x}\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$${y}−{x}\frac{{dy}}{{dx}}=−{xy}^{\mathrm{2}} \\ $$$$\frac{{ydx}−{xdy}}{{y}^{\mathrm{2}} }=−{xdx} \\ $$$${d}\left(\frac{{x}}{{y}}\right)=−{xdx} \\ $$$$\int{d}\left(\frac{{x}}{{y}}\right)=−\int{xdx} \\ $$$$\frac{{x}}{{y}}=\frac{−{x}^{\mathrm{2}} }{\mathrm{2}}+{c} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 14/Dec/18
c)x=e^t (dx/dt)=e^t (dy/dx)=(dy/dt)×(dt/dx)=(1/e^t )(dy/dt) e^t (dy/dx)=(dy/dt) x(dy/dx)=(dy/dt) (d/dx)((dy/dx))=(d/dt)((dy/dx))×(dt/dx) =(d/dt)((1/e^t )×(dy/dt))×(1/e^t ) =(1/e^t )[(1/e^t )×(d^2 y/dt^2 )+(dy/dt)×e^(−t) ×−1] =((1/e^t ))^2 ×(d^2 y/dt^2 )−((1/e^t ))^2 ×(dy/dt) (e^t )^2 (d^2 y/dx^2 )=(d^2 y/dt^2 )−(dy/dt) let (d/dt)=θ x^2 (d^2 y/dx^2 )=(θ^2 −θ)y wait busy...
$$\left.{c}\right){x}={e}^{{t}} \:\:\:\frac{{dx}}{{dt}}={e}^{{t}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{dy}}{{dt}}×\frac{{dt}}{{dx}}=\frac{\mathrm{1}}{{e}^{{t}} }\frac{{dy}}{{dt}} \\ $$$${e}^{{t}} \frac{{dy}}{{dx}}=\frac{{dy}}{{dt}} \\ $$$${x}\frac{{dy}}{{dx}}=\frac{{dy}}{{dt}} \\ $$$$\frac{{d}}{{dx}}\left(\frac{{dy}}{{dx}}\right)=\frac{{d}}{{dt}}\left(\frac{{dy}}{{dx}}\right)×\frac{{dt}}{{dx}} \\ $$$$=\frac{{d}}{{dt}}\left(\frac{\mathrm{1}}{{e}^{{t}} }×\frac{{dy}}{{dt}}\right)×\frac{\mathrm{1}}{{e}^{{t}} } \\ $$$$=\frac{\mathrm{1}}{{e}^{{t}} }\left[\frac{\mathrm{1}}{{e}^{{t}} }×\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }+\frac{{dy}}{{dt}}×{e}^{−{t}} ×−\mathrm{1}\right] \\ $$$$=\left(\frac{\mathrm{1}}{{e}^{{t}} }\right)^{\mathrm{2}} ×\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }−\left(\frac{\mathrm{1}}{{e}^{{t}} }\right)^{\mathrm{2}} ×\frac{{dy}}{{dt}} \\ $$$$\left({e}^{{t}} \right)^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }−\frac{{dy}}{{dt}} \\ $$$${let}\:\frac{{d}}{{dt}}=\theta\: \\ $$$${x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\left(\theta^{\mathrm{2}} −\theta\right){y} \\ $$$${wait}\:{busy}… \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 14/Dec/18
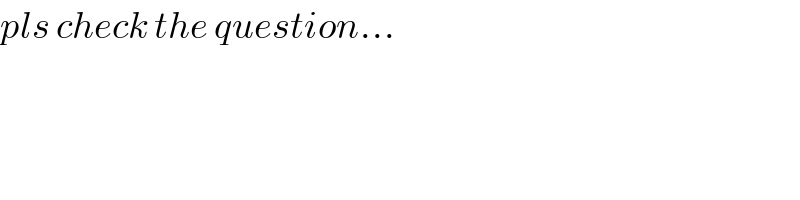
pls check the question...
$${pls}\:{check}\:{the}\:{question}… \\ $$
Commented by peter frank last updated on 14/Dec/18
yes sir am arleady check
$$\mathrm{yes}\:\mathrm{sir}\:\mathrm{am}\:\mathrm{arleady}\:\mathrm{check}\: \\ $$
Answered by peter frank last updated on 14/Dec/18
c) y=vx (dy/dx)=v+x(dv/dx) ......(i) (d^2 y/dx^2 )=2(dv/dx) +x(d^2 y/dx^2 )....(ii) x^2 (d^2 y/dx^(2 ) )−2x(dy/dx)+2(2x^2 +1)y=24x^3 x^2 (2(dv/dx)+x(d^2 y/dx^2 ))−2x(v+x(dv/dx))+2vx(2x^2 +1)=24x^3 x^3 (d^2 v/dx^2 )+4vx^3 =24x^3 (d^2 v/dx^2 )+4v=24 (d^2 v/dx^2 )+4(v−6)=0 t=u−6 (dt/dx)=(du/dx) (d^2 t/dx^2 )=(d^2 u/dx^2 ) t^2 +4t=0 t=0±2i t=e^(px) (Acos qx+Bsin qx)= t=Acos 2x+Bsin 2x u−6=Acos 2x+Bsin 2x (y/x)−6=Acos 2x+Bsin 2x y=Acos 2x+Bsin 2x+6x .....(i) (dy/dx)=−2Axsin 2x+Acos 2x+2Bxcos 2x+Bsin 2x.....(ii) (d^2 y/dx^2 )=−4Axcos2x−2Asin 2x−2Asin 2x+2Bcos 2x−4Bxsin 2x.....(iii) from ii) (dy/dx)=−2Axsin 2x+Acos 2x+2Bxcos 2x+Bsin 2x.....(ii) given x=0,(dy/dx)=6 6=A+6 A=0 from iii (d^2 y/dx^2 )=−4Axcos2x−2Asin 2x−2Asin 2x+2Bcos 2x−4Bxsin 2x.....(iii) 4=2B+2B B=1 from( i) y=Acos 2x+Bsin 2x+6x .....(i) put A=0 B=1 y=xsin 2x+6x required solution
$$\left.\mathrm{c}\right)\:{y}={vx} \\ $$$$\frac{{dy}}{{dx}}={v}+{x}\frac{{dv}}{{dx}}\:……\left({i}\right) \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\mathrm{2}\frac{{dv}}{{dx}}\:\:+{x}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }….\left({ii}\right) \\ $$$$\:{x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}\:} }−\mathrm{2}{x}\frac{{dy}}{{dx}}+\mathrm{2}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right){y}=\mathrm{24}{x}^{\mathrm{3}} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{2}\frac{{dv}}{{dx}}+{x}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\right)−\mathrm{2}{x}\left({v}+{x}\frac{{dv}}{{dx}}\right)+\mathrm{2}{vx}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{24}{x}^{\mathrm{3}} \\ $$$${x}^{\mathrm{3}} \frac{{d}^{\mathrm{2}} {v}}{{dx}^{\mathrm{2}} }+\mathrm{4}{vx}^{\mathrm{3}} =\mathrm{24}{x}^{\mathrm{3}} \\ $$$$\frac{{d}^{\mathrm{2}} {v}}{{dx}^{\mathrm{2}} }+\mathrm{4}{v}=\mathrm{24} \\ $$$$\frac{{d}^{\mathrm{2}} {v}}{{dx}^{\mathrm{2}} }+\mathrm{4}\left({v}−\mathrm{6}\right)=\mathrm{0} \\ $$$${t}={u}−\mathrm{6} \\ $$$$\frac{{dt}}{{dx}}=\frac{{du}}{{dx}} \\ $$$$\frac{{d}^{\mathrm{2}} {t}}{{dx}^{\mathrm{2}} }=\frac{{d}^{\mathrm{2}} {u}}{{dx}^{\mathrm{2}} } \\ $$$${t}^{\mathrm{2}} +\mathrm{4}{t}=\mathrm{0} \\ $$$${t}=\mathrm{0}\pm\mathrm{2}{i} \\ $$$${t}={e}^{{px}} \left({A}\mathrm{cos}\:\mathrm{qx}+{B}\mathrm{sin}\:{qx}\right)= \\ $$$${t}={A}\mathrm{cos}\:\mathrm{2}{x}+{B}\mathrm{sin}\:\mathrm{2}{x} \\ $$$${u}−\mathrm{6}={A}\mathrm{cos}\:\mathrm{2}{x}+{B}\mathrm{sin}\:\mathrm{2}{x} \\ $$$$\frac{{y}}{{x}}−\mathrm{6}={A}\mathrm{cos}\:\mathrm{2}{x}+{B}\mathrm{sin}\:\mathrm{2}{x} \\ $$$${y}={A}\mathrm{cos}\:\mathrm{2}{x}+{B}\mathrm{sin}\:\mathrm{2}{x}+\mathrm{6}{x}\:…..\left(\mathrm{i}\right) \\ $$$$\frac{{dy}}{{dx}}=−\mathrm{2}{Ax}\mathrm{sin}\:\mathrm{2}{x}+{A}\mathrm{cos}\:\mathrm{2}{x}+\mathrm{2}{Bx}\mathrm{cos}\:\mathrm{2}{x}+{B}\mathrm{sin}\:\mathrm{2}{x}…..\left(\mathrm{ii}\right) \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=−\mathrm{4}{A}\mathrm{xcos2x}−\mathrm{2Asin}\:\mathrm{2x}−\mathrm{2Asin}\:\mathrm{2x}+\mathrm{2Bcos}\:\mathrm{2x}−\mathrm{4Bxsin}\:\mathrm{2x}…..\left(\mathrm{iii}\right) \\ $$$$\left.{from}\:{ii}\right) \\ $$$$\frac{{dy}}{{dx}}=−\mathrm{2}{Ax}\mathrm{sin}\:\mathrm{2}{x}+{A}\mathrm{cos}\:\mathrm{2}{x}+\mathrm{2}{Bx}\mathrm{cos}\:\mathrm{2}{x}+{B}\mathrm{sin}\:\mathrm{2}{x}…..\left(\mathrm{ii}\right) \\ $$$${given}\:{x}=\mathrm{0},\frac{{dy}}{{dx}}=\mathrm{6}\: \\ $$$$\mathrm{6}={A}+\mathrm{6}\:\:\mathrm{A}=\mathrm{0} \\ $$$${from}\:{iii} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=−\mathrm{4}{A}\mathrm{xcos2x}−\mathrm{2Asin}\:\mathrm{2x}−\mathrm{2Asin}\:\mathrm{2x}+\mathrm{2Bcos}\:\mathrm{2x}−\mathrm{4Bxsin}\:\mathrm{2x}…..\left(\mathrm{iii}\right) \\ $$$$\mathrm{4}=\mathrm{2}{B}+\mathrm{2}{B}\:\:\:\:\mathrm{B}=\mathrm{1} \\ $$$${from}\left(\:{i}\right) \\ $$$${y}={A}\mathrm{cos}\:\mathrm{2}{x}+{B}\mathrm{sin}\:\mathrm{2}{x}+\mathrm{6}{x}\:…..\left(\mathrm{i}\right) \\ $$$${put}\:{A}=\mathrm{0}\:\:\:\:{B}=\mathrm{1} \\ $$$${y}={x}\mathrm{sin}\:\mathrm{2}{x}+\mathrm{6}{x} \\ $$$${required}\:{solution} \\ $$$$ \\ $$$$ \\ $$
Answered by peter frank last updated on 14/Dec/18
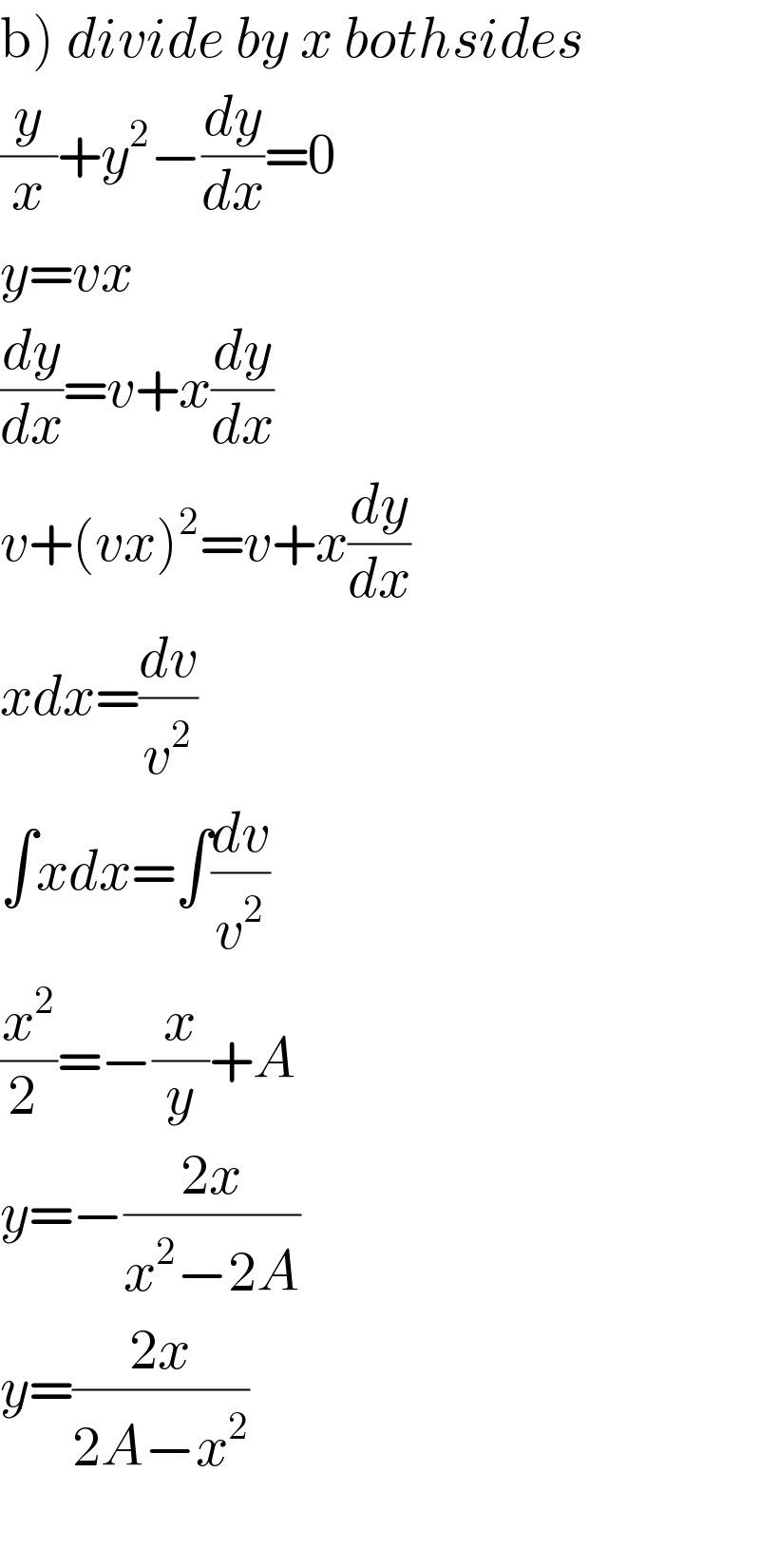
b) divide by x bothsides (y/x)+y^2 −(dy/dx)=0 y=vx (dy/dx)=v+x(dy/dx) v+(vx)^2 =v+x(dy/dx) xdx=(dv/v^2 ) ∫xdx=∫(dv/v^2 ) (x^2 /(2 ))=−(x/y)+A y=−((2x)/(x^2 −2A)) y=((2x)/(2A−x^2 ))
$$\left.\mathrm{b}\right)\:{divide}\:{by}\:{x}\:{bothsides} \\ $$$$\frac{{y}}{{x}}+{y}^{\mathrm{2}} −\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$${y}={vx} \\ $$$$\frac{{dy}}{{dx}}={v}+{x}\frac{{dy}}{{dx}} \\ $$$${v}+\left({vx}\right)^{\mathrm{2}} ={v}+{x}\frac{{dy}}{{dx}} \\ $$$${xdx}=\frac{{dv}}{{v}^{\mathrm{2}} } \\ $$$$\int{xdx}=\int\frac{{dv}}{{v}^{\mathrm{2}} } \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{2}\:}=−\frac{{x}}{{y}}+{A} \\ $$$${y}=−\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} −\mathrm{2}{A}} \\ $$$${y}=\frac{\mathrm{2}{x}}{\mathrm{2}{A}−{x}^{\mathrm{2}} } \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *