Question Number 175888 by Mastermind last updated on 08/Sep/22
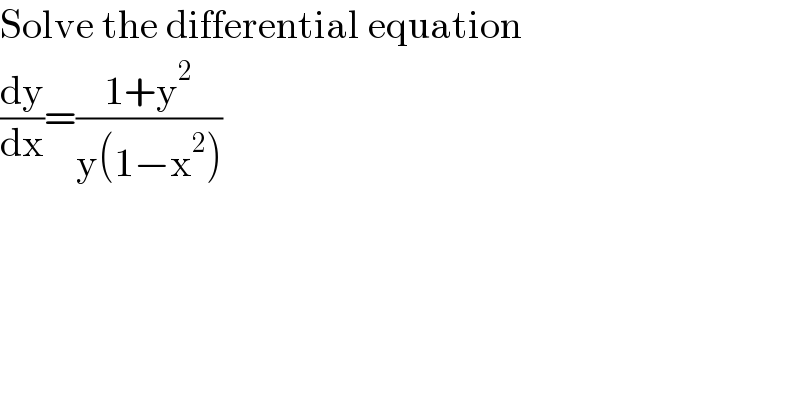
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equation} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }{\mathrm{y}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)} \\ $$
Answered by mahdipoor last updated on 08/Sep/22
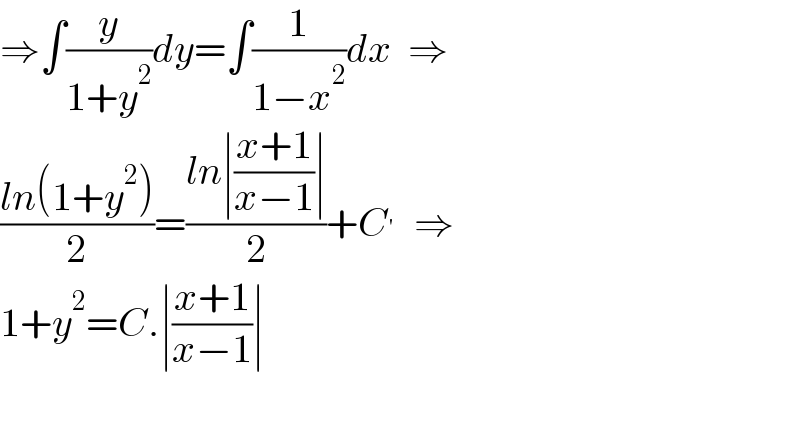
$$\Rightarrow\int\frac{{y}}{\mathrm{1}+{y}^{\mathrm{2}} }{dy}=\int\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}\:\:\Rightarrow \\ $$$$\frac{{ln}\left(\mathrm{1}+{y}^{\mathrm{2}} \right)}{\mathrm{2}}=\frac{{ln}\mid\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\mid}{\mathrm{2}}+{C}^{'} \:\:\Rightarrow\: \\ $$$$\mathrm{1}+{y}^{\mathrm{2}} ={C}.\mid\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\mid \\ $$$$ \\ $$
