Question Number 165849 by daus last updated on 09/Feb/22
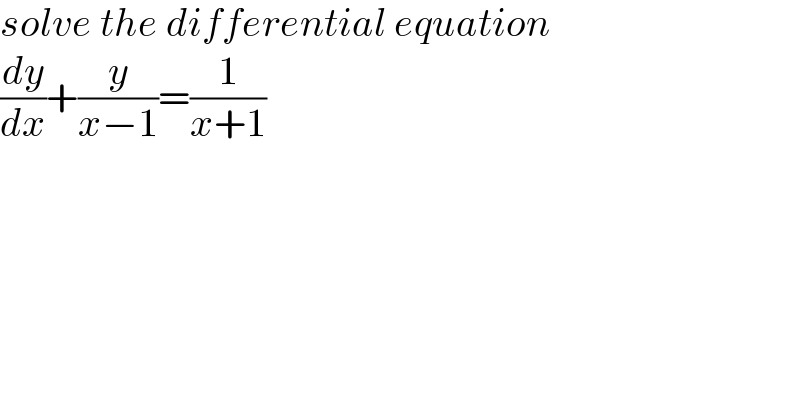
$${solve}\:{the}\:{differential}\:{equation} \\ $$$$\frac{{dy}}{{dx}}+\frac{{y}}{{x}−\mathrm{1}}=\frac{\mathrm{1}}{{x}+\mathrm{1}} \\ $$
Commented by mkam last updated on 10/Feb/22

$$\boldsymbol{{p}}\left(\boldsymbol{{x}}\right)=\:\frac{\mathrm{1}}{\boldsymbol{{x}}−\mathrm{1}}\:\:,\:\boldsymbol{{Q}}\left(\boldsymbol{{x}}\right)\:=\:\frac{\mathrm{1}}{\boldsymbol{{x}}+\mathrm{1}} \\ $$$$ \\ $$$$\left(\boldsymbol{{I}}.\boldsymbol{{f}}\right)\:=\:\boldsymbol{{e}}^{\int\boldsymbol{{P}}\left(\boldsymbol{{x}}\right)\boldsymbol{{dx}}} \:=\:\boldsymbol{{e}}\:^{\int\:\frac{\mathrm{1}}{\boldsymbol{{x}}−\mathrm{1}}\:\boldsymbol{{dx}}} =\:\boldsymbol{{e}}^{\boldsymbol{{ln}}\mid\boldsymbol{{x}}−\mathrm{1}\mid\:} =\:\boldsymbol{{x}}−\mathrm{1} \\ $$$$ \\ $$$$\left(\boldsymbol{{I}}.\boldsymbol{{f}}\right)\:\boldsymbol{{y}}\:=\:\int\:\left(\boldsymbol{{I}}.\boldsymbol{{f}}\right)\:.\:\boldsymbol{{Q}}\left(\boldsymbol{{x}}\right)\:\boldsymbol{{dx}} \\ $$$$ \\ $$$$\left(\boldsymbol{{x}}−\mathrm{1}\right)\boldsymbol{{y}}\:=\:\int\:\left(\:\frac{\boldsymbol{{x}}−\mathrm{1}}{\boldsymbol{{x}}+\mathrm{1}}\right)\boldsymbol{{dx}}\Rightarrow\:\left(\:\boldsymbol{{x}}−\mathrm{1}\right)\:\boldsymbol{{y}}\:=\:\int\:\left(\mathrm{1}\:−\:\frac{\mathrm{2}}{\boldsymbol{{x}}+\mathrm{1}}\right)\boldsymbol{{dx}} \\ $$$$ \\ $$$$\therefore\left(\:\boldsymbol{{x}}\:−\:\mathrm{1}\:\right)\boldsymbol{{y}}\:=\:\boldsymbol{{x}}\:−\mathrm{2}\:\boldsymbol{{ln}}\:\mid\:\boldsymbol{{x}}\:+\mathrm{1}\:\mid\:+\:\boldsymbol{{C}} \\ $$$$ \\ $$$$\boldsymbol{{y}}\:=\:\frac{\boldsymbol{{x}}}{\boldsymbol{{x}}−\mathrm{1}}\:−\:\frac{\mathrm{2}\:\boldsymbol{{ln}}\mid\boldsymbol{{x}}+\mathrm{1}\mid}{\boldsymbol{{x}}−\mathrm{1}}\:+\:\frac{\boldsymbol{{C}}}{\boldsymbol{{x}}\:−\:\mathrm{1}} \\ $$$$ \\ $$$$\square\:\boldsymbol{{mohammad}}\:\boldsymbol{{aldolaimy}} \\ $$
