Question Number 95600 by Tony Lin last updated on 26/May/20
$${solve}\:{the}\:{differential}\:{equation} \\ $$$${L}\frac{{d}^{\mathrm{2}} {q}}{{dt}^{\mathrm{2}} }+{R}\frac{{dq}}{{dt}}+\frac{\mathrm{1}}{{C}}{q}=\varepsilon{cos}\omega{t} \\ $$$${which}\:{is}\:{in}\:{R}.{L}.{C}\:{circuit}\:{with}\:{forced}\:{oscillation} \\ $$$${where}\:{L}\:{is}\:{inductance} \\ $$$${R}\:{is}\:{resistance} \\ $$$${C}\:{is}\:{capacitanace} \\ $$$${q}\:{is}\:{charge} \\ $$$$\varepsilon\:{is}\:{motion}\:{emf} \\ $$$${t}\:{is}\:{time} \\ $$
Answered by mathmax by abdo last updated on 26/May/20
![we take q=x and L =δ so (e)⇒δx^(′′) +r x^′ +cx =ξcos(wt) (c=(1/C)) let solve by laplace transform ⇒ δL(x^(′′) )+rL(x^′ )+cL(x) =ξL(cos(wt)) ⇒ δ(t^2 L(x)−tx(0)−x^′ (0))+r(tL(x)−x(0))+cL(x) =ξL(cos(wt)) ⇒ (δt^2 +rt +c)L(x)−δt x(0)−δx^′ (0)−rx(0) =ξL(cos(wt) L(cos(wt) =∫_0 ^∞ cos(wu)e^(−tu) du =Re(∫_0 ^∞ e^(iwu−tu) du) but ∫_0 ^∞ e^((iw−t)u) du =[(1/(iw−t)) e^((−t+iw)u) ]_0 ^∞ =−(1/(iw−t)) =(1/(t−iw)) =((t+iw)/(t^2 +w^2 )) ⇒L(cos(wt)) =(t/(t^2 +w^2 )) ⇒ (δt^2 +rt +c)L(x) =((ξt)/(t^2 +w^2 )) +(δt +r)x(0)+δx^′ (0) ⇒ L(x) =((ξt)/((t^2 +w^2 )(δt^2 +rt +c))) +((δt +r)/(δt^2 +rt +c))x(0) +((δx^′ (0))/(δt^2 +rt +c)) ⇒ x(t) =ξL^(−1) ((1/((t^2 +w^2 )(δt^2 +rt +c)))) +L^(−1) (((δt +r)/(δt^2 +rt +c))x(0)) +L^(−1) ( ((δx^′ (0))/(δt^2 +rt +c))) δt^2 +rt +c =0→Δ =r^2 −4δc if Δ>0 ⇒t_1 =((−r +(√(r^2 −4δc)))/(2δ)) and t_2 =((−r−(√(r^2 −4δc)))/(2δ)) ⇒ ((δx^′ (0))/(δt^2 +rt +c)) =((x^′ (0))/((t−t_1 )(t−t_2 ))) =δ((x^′ (0))/( (√(r^2 −4δc))))((1/(t−t_1 ))−(1/(t−t_2 ))) ⇒ L^(−1) (....) =((δx^′ (0))/( (√(r^2 −4δc)))){ L^(−1) ((1/(t−t_1 )))−L^(−1) ((1/(t−t_2 )))} =((δx^′ (0))/( (√(r^2 −4δc)))){e^(t_1 t) −e^(t_2 t) }...be continued....](https://www.tinkutara.com/question/Q95623.png)
$$\mathrm{we}\:\mathrm{take}\:\mathrm{q}=\mathrm{x}\:\mathrm{and}\:\mathrm{L}\:=\delta\:\:\mathrm{so}\:\left(\mathrm{e}\right)\Rightarrow\delta\mathrm{x}^{''} \:+\mathrm{r}\:\mathrm{x}^{'} \:+\mathrm{cx}\:=\xi\mathrm{cos}\left(\mathrm{wt}\right)\:\left(\mathrm{c}=\frac{\mathrm{1}}{\mathrm{C}}\right) \\ $$$$\mathrm{let}\:\mathrm{solve}\:\mathrm{by}\:\mathrm{laplace}\:\mathrm{transform}\:\Rightarrow \\ $$$$\delta\mathrm{L}\left(\mathrm{x}^{''} \right)+\mathrm{rL}\left(\mathrm{x}^{'} \right)+\mathrm{cL}\left(\mathrm{x}\right)\:=\xi\mathrm{L}\left(\mathrm{cos}\left(\mathrm{wt}\right)\right)\:\Rightarrow \\ $$$$\delta\left(\mathrm{t}^{\mathrm{2}} \mathrm{L}\left(\mathrm{x}\right)−\mathrm{tx}\left(\mathrm{0}\right)−\mathrm{x}^{'} \left(\mathrm{0}\right)\right)+\mathrm{r}\left(\mathrm{tL}\left(\mathrm{x}\right)−\mathrm{x}\left(\mathrm{0}\right)\right)+\mathrm{cL}\left(\mathrm{x}\right)\:=\xi\mathrm{L}\left(\mathrm{cos}\left(\mathrm{wt}\right)\right)\:\Rightarrow \\ $$$$\left(\delta\mathrm{t}^{\mathrm{2}} +\mathrm{rt}\:+\mathrm{c}\right)\mathrm{L}\left(\mathrm{x}\right)−\delta\mathrm{t}\:\mathrm{x}\left(\mathrm{0}\right)−\delta\mathrm{x}^{'} \left(\mathrm{0}\right)−\mathrm{rx}\left(\mathrm{0}\right)\:=\xi\mathrm{L}\left(\mathrm{cos}\left(\mathrm{wt}\right)\right. \\ $$$$\mathrm{L}\left(\mathrm{cos}\left(\mathrm{wt}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{cos}\left(\mathrm{wu}\right)\mathrm{e}^{−\mathrm{tu}} \:\mathrm{du}\right. \\ $$$$=\mathrm{Re}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\mathrm{iwu}−\mathrm{tu}} \mathrm{du}\right)\:\mathrm{but}\:\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(\mathrm{iw}−\mathrm{t}\right)\mathrm{u}} \:\mathrm{du}\:=\left[\frac{\mathrm{1}}{\mathrm{iw}−\mathrm{t}}\:\mathrm{e}^{\left(−\mathrm{t}+\mathrm{iw}\right)\mathrm{u}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{iw}−\mathrm{t}}\:=\frac{\mathrm{1}}{\mathrm{t}−\mathrm{iw}}\:=\frac{\mathrm{t}+\mathrm{iw}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{w}^{\mathrm{2}} }\:\Rightarrow\mathrm{L}\left(\mathrm{cos}\left(\mathrm{wt}\right)\right)\:=\frac{\mathrm{t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{w}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\left(\delta\mathrm{t}^{\mathrm{2}} \:+\mathrm{rt}\:+\mathrm{c}\right)\mathrm{L}\left(\mathrm{x}\right)\:=\frac{\xi\mathrm{t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{w}^{\mathrm{2}} }\:+\left(\delta\mathrm{t}\:+\mathrm{r}\right)\mathrm{x}\left(\mathrm{0}\right)+\delta\mathrm{x}^{'} \left(\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{x}\right)\:=\frac{\xi\mathrm{t}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{w}^{\mathrm{2}} \right)\left(\delta\mathrm{t}^{\mathrm{2}} \:+\mathrm{rt}\:+\mathrm{c}\right)}\:+\frac{\delta\mathrm{t}\:+\mathrm{r}}{\delta\mathrm{t}^{\mathrm{2}} \:+\mathrm{rt}\:+\mathrm{c}}\mathrm{x}\left(\mathrm{0}\right)\:+\frac{\delta\mathrm{x}^{'} \left(\mathrm{0}\right)}{\delta\mathrm{t}^{\mathrm{2}} \:+\mathrm{rt}\:+\mathrm{c}}\:\Rightarrow \\ $$$$\mathrm{x}\left(\mathrm{t}\right)\:=\xi\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{w}^{\mathrm{2}} \right)\left(\delta\mathrm{t}^{\mathrm{2}} \:+\mathrm{rt}\:+\mathrm{c}\right)}\right)\:+\mathrm{L}^{−\mathrm{1}} \left(\frac{\delta\mathrm{t}\:+\mathrm{r}}{\delta\mathrm{t}^{\mathrm{2}} \:+\mathrm{rt}\:+\mathrm{c}}\mathrm{x}\left(\mathrm{0}\right)\right) \\ $$$$+\mathrm{L}^{−\mathrm{1}} \left(\:\frac{\delta\mathrm{x}^{'} \left(\mathrm{0}\right)}{\delta\mathrm{t}^{\mathrm{2}} \:+\mathrm{rt}\:+\mathrm{c}}\right) \\ $$$$\delta\mathrm{t}^{\mathrm{2}} \:+\mathrm{rt}\:+\mathrm{c}\:=\mathrm{0}\rightarrow\Delta\:=\mathrm{r}^{\mathrm{2}} −\mathrm{4}\delta\mathrm{c} \\ $$$$\mathrm{if}\:\Delta>\mathrm{0}\:\Rightarrow\mathrm{t}_{\mathrm{1}} =\frac{−\mathrm{r}\:+\sqrt{\mathrm{r}^{\mathrm{2}} −\mathrm{4}\delta\mathrm{c}}}{\mathrm{2}\delta}\:\mathrm{and}\:\mathrm{t}_{\mathrm{2}} =\frac{−\mathrm{r}−\sqrt{\mathrm{r}^{\mathrm{2}} −\mathrm{4}\delta\mathrm{c}}}{\mathrm{2}\delta}\:\Rightarrow \\ $$$$\frac{\delta\mathrm{x}^{'} \left(\mathrm{0}\right)}{\delta\mathrm{t}^{\mathrm{2}} +\mathrm{rt}\:+\mathrm{c}}\:=\frac{\mathrm{x}^{'} \left(\mathrm{0}\right)}{\left(\mathrm{t}−\mathrm{t}_{\mathrm{1}} \right)\left(\mathrm{t}−\mathrm{t}_{\mathrm{2}} \right)}\:=\delta\frac{\mathrm{x}^{'} \left(\mathrm{0}\right)}{\:\sqrt{\mathrm{r}^{\mathrm{2}} −\mathrm{4}\delta\mathrm{c}}}\left(\frac{\mathrm{1}}{\mathrm{t}−\mathrm{t}_{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{t}−\mathrm{t}_{\mathrm{2}} }\right)\:\Rightarrow \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(….\right)\:=\frac{\delta\mathrm{x}^{'} \left(\mathrm{0}\right)}{\:\sqrt{\mathrm{r}^{\mathrm{2}} −\mathrm{4}\delta\mathrm{c}}}\left\{\:\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{t}−\mathrm{t}_{\mathrm{1}} }\right)−\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{t}−\mathrm{t}_{\mathrm{2}} }\right)\right\} \\ $$$$=\frac{\delta\mathrm{x}^{'} \left(\mathrm{0}\right)}{\:\sqrt{\mathrm{r}^{\mathrm{2}} −\mathrm{4}\delta\mathrm{c}}}\left\{\mathrm{e}^{\mathrm{t}_{\mathrm{1}} \mathrm{t}} −\mathrm{e}^{\mathrm{t}_{\mathrm{2}} \mathrm{t}} \right\}…\mathrm{be}\:\mathrm{continued}…. \\ $$
Commented by mathmax by abdo last updated on 26/May/20
$$\mathrm{wroskien}\:\mathrm{method}\:\:\left(\mathrm{e}\right)\:\Rightarrow\mathrm{x}^{''} \:+\frac{\mathrm{r}}{\delta}\mathrm{x}^{'} \:+\frac{\mathrm{c}}{\delta}\:\mathrm{x}\:=\frac{\xi}{\delta}\mathrm{cos}\left(\mathrm{wt}\right) \\ $$$$\left(\mathrm{he}\right)\rightarrow\mathrm{r}^{\mathrm{2}} \:+\frac{\mathrm{r}}{\delta}\mathrm{r}\:+\frac{\mathrm{c}}{\delta}\:=\mathrm{0}\:\rightarrow\Delta\:=\frac{\mathrm{r}^{\mathrm{2}} }{\delta^{\mathrm{2}} }\:−\frac{\mathrm{4c}}{\delta}\: \\ $$$$\mathrm{if}\:\Delta>\mathrm{0}\:\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\frac{−\frac{\mathrm{r}}{\delta}+\sqrt{\Delta}}{\mathrm{2}}\:\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\frac{−\frac{\mathrm{r}}{\delta}−\sqrt{\Delta}}{\mathrm{2}} \\ $$$$\mathrm{y}_{\mathrm{h}} =\alpha\mathrm{e}^{\mathrm{r}_{\mathrm{1}} \mathrm{t}} \:+\beta\:\mathrm{e}^{\mathrm{r}_{\mathrm{2}} \mathrm{t}} \:=\alpha\mathrm{u}_{\mathrm{1}} +\beta\mathrm{u}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{u}_{\mathrm{1}} \:\:\:\:\:\:\:\mathrm{u}_{\mathrm{2}} }\\{\mathrm{u}_{\mathrm{1}} ^{'} \:\:\:\:\:\:\:\:\mathrm{u}_{\mathrm{2}} ^{'} }\end{vmatrix}\:=\begin{vmatrix}{\mathrm{e}^{\mathrm{r}_{\mathrm{1}} \mathrm{t}} \:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{r}_{\mathrm{2}} \mathrm{t}} \:}\\{\mathrm{r}_{\mathrm{1}} \mathrm{e}^{\mathrm{r}_{\mathrm{1}} \mathrm{t}} \:\:\:\mathrm{r}_{\mathrm{2}} \mathrm{e}^{\mathrm{r}_{\mathrm{2}} \mathrm{t}} }\end{vmatrix} \\ $$$$=\left(\mathrm{r}_{\mathrm{2}} −\mathrm{r}_{\mathrm{1}} \right)\mathrm{e}^{\left(\mathrm{r}_{\mathrm{1}} +\mathrm{r}_{\mathrm{2}} \right)\mathrm{t}} \:\:=\sqrt{\Delta}\mathrm{e}^{−\frac{\mathrm{r}}{\delta}\mathrm{t}} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{r}_{\mathrm{2}} \mathrm{t}\:} }\\{\frac{\xi}{\delta}\mathrm{cos}\left(\mathrm{wt}\right)\:\:\:\:\mathrm{r}_{\mathrm{2}} \mathrm{e}^{\mathrm{r}_{\mathrm{2}} \mathrm{t}} }\end{vmatrix}=−\frac{\xi}{\delta}\mathrm{cos}\left(\mathrm{wt}\right)\mathrm{e}^{\mathrm{r}_{\mathrm{2}} \mathrm{t}} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{r}_{\mathrm{1}} \mathrm{t}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{r}_{\mathrm{1}} \mathrm{e}^{\mathrm{r}_{\mathrm{1}} \mathrm{t}} \:\:\:\:\:\:\:\frac{\xi}{\delta}\mathrm{cos}\left(\mathrm{wt}\right)}\end{vmatrix}=\frac{\xi}{\delta}\mathrm{cos}\left(\mathrm{wt}\right)\mathrm{e}^{\mathrm{r}_{\mathrm{1}} \mathrm{t}} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{W}}\mathrm{dt}\:=−\frac{\xi}{\delta}\int\:\:\frac{\mathrm{cos}\left(\mathrm{wt}\right)\mathrm{e}^{\mathrm{r}_{\mathrm{2}} \mathrm{t}} }{\:\sqrt{\Delta}\mathrm{e}^{−\frac{\mathrm{r}}{\delta}\mathrm{t}} }\:=−\frac{\xi}{\delta\sqrt{\Delta}}\:\int\:\mathrm{cos}\left(\mathrm{wt}\right)\mathrm{e}^{\left(\mathrm{r}_{\mathrm{2}} +\frac{\mathrm{r}}{\delta}\right)\mathrm{t}} \mathrm{dt} \\ $$$$=−\frac{\xi}{\delta\sqrt{\Delta}}\mathrm{Re}\left(\int\:\:\mathrm{e}^{\mathrm{iwt}+\left(\mathrm{r}_{\mathrm{2}} +\frac{\mathrm{r}}{\delta}\right)\mathrm{t}} \mathrm{dt}\right)=…. \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{W}}\mathrm{dt}\:=\frac{\xi}{\delta\sqrt{\Delta}}\int\:\:\:\frac{\mathrm{cos}\left(\mathrm{wt}\right)\mathrm{e}^{\mathrm{r}_{\mathrm{1}} \mathrm{t}} }{\mathrm{e}^{−\frac{\mathrm{r}}{\delta}} }\:\mathrm{dt}\:=\frac{\xi}{\delta\sqrt{\Delta}}\:\int\:\mathrm{cos}\left(\mathrm{wt}\right)\mathrm{e}^{\left(\mathrm{r}_{\mathrm{1}} +\frac{\mathrm{r}}{\delta}\right)\mathrm{t}} \:\mathrm{dt} \\ $$$$…\:\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$
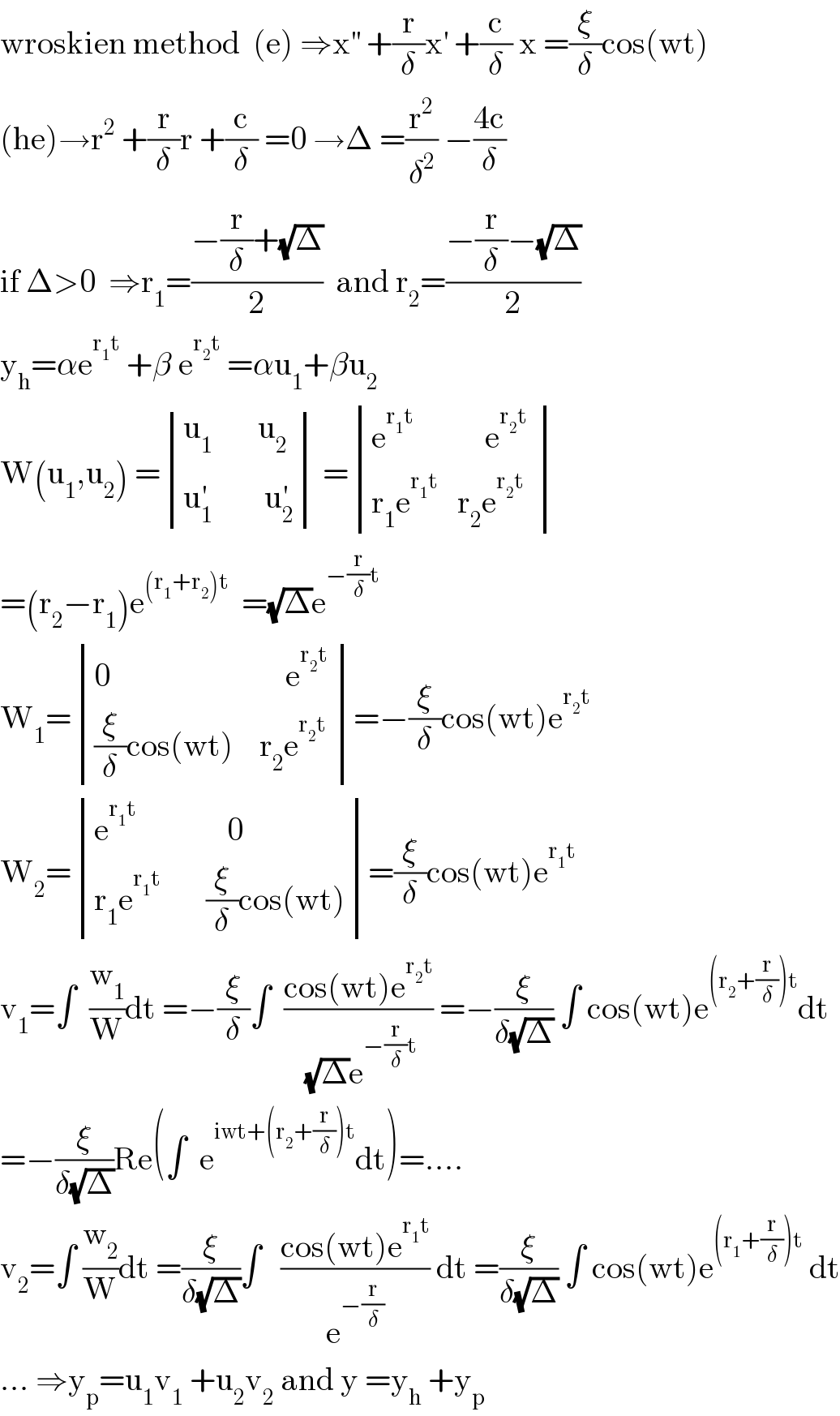
Commented by Tony Lin last updated on 26/May/20
$${thanks}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 27/May/20
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}. \\ $$