Question Number 181218 by Mastermind last updated on 23/Nov/22

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{Differential}\:\mathrm{equation}: \\ $$$$\mathrm{x}\frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{y}=\mathrm{2y}\left(\mathrm{lnx}−\mathrm{lny}\right) \\ $$$$ \\ $$$$. \\ $$
Answered by qaz last updated on 23/Nov/22
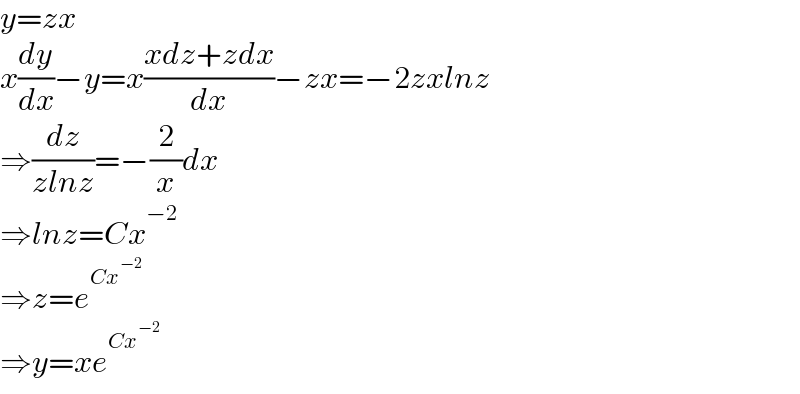
$${y}={zx} \\ $$$${x}\frac{{dy}}{{dx}}−{y}={x}\frac{{xdz}+{zdx}}{{dx}}−{zx}=−\mathrm{2}{zxlnz} \\ $$$$\Rightarrow\frac{{dz}}{{zlnz}}=−\frac{\mathrm{2}}{{x}}{dx} \\ $$$$\Rightarrow{lnz}={Cx}^{−\mathrm{2}} \\ $$$$\Rightarrow{z}={e}^{{Cx}^{−\mathrm{2}} } \\ $$$$\Rightarrow{y}={xe}^{{Cx}^{−\mathrm{2}} } \\ $$
Commented by universe last updated on 23/Nov/22

$${good}\:{solution}\:{sir} \\ $$
