Question Number 175036 by Mastermind last updated on 16/Aug/22
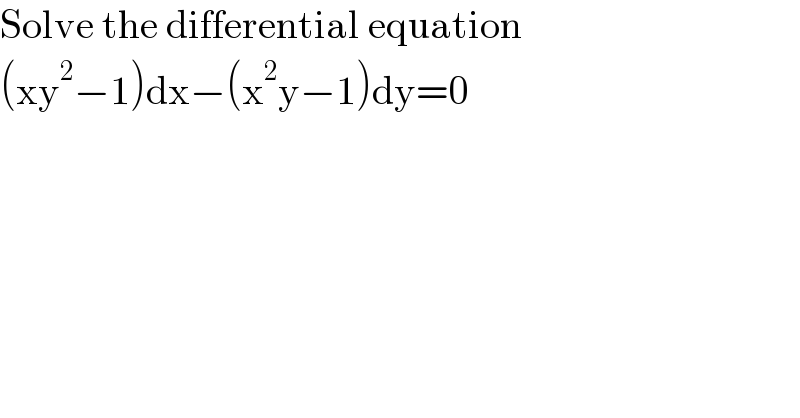
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equation} \\ $$$$\left(\mathrm{xy}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{dx}−\left(\mathrm{x}^{\mathrm{2}} \mathrm{y}−\mathrm{1}\right)\mathrm{dy}=\mathrm{0} \\ $$
Answered by ajfour last updated on 17/Aug/22

$${xy}\left({ydx}−{xdy}\right)={dx}−{dy} \\ $$$$\Rightarrow\:\:{xy}^{\mathrm{3}} {d}\left(\frac{{x}}{{y}}\right)={d}\left({x}−{y}\right) \\ $$$$\Rightarrow\:\:{y}^{\mathrm{4}} \left(\frac{{x}}{{y}}\right){d}\left(\frac{{x}}{{y}}\right)={d}\left({x}−{y}\right) \\ $$$$\:\:\:\:\:\:\:{x}^{\mathrm{4}} \left(\frac{{y}}{{x}}\right)^{\mathrm{3}} {d}\left(\frac{{x}}{{y}}\right)={d}\left({x}−{y}\right) \\ $$$$\:\:\:\:−\mathrm{3}{x}^{\mathrm{3}} {y}\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} {d}\left(\frac{{x}}{{y}}\right)=−\mathrm{3}{d}\left({x}−{y}\right) \\ $$$$\:\:\:\mathrm{3}{xy}^{\mathrm{3}} {d}\left(\frac{{x}}{{y}}\right)=\mathrm{3}{d}\left({x}−{y}\right) \\ $$$${rearranging}\:\&\:{adding} \\ $$$${and}\:{with}\:\:\:{t}=\frac{{x}}{{y}} \\ $$$$\left({x}−{y}\right)^{\mathrm{4}} {dt}=\left(\mathrm{3}+\frac{\mathrm{1}}{{t}}+{t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} \right){d}\left({x}−{y}\right) \\ $$$${say}\:{if}\:{x}−{y}={z} \\ $$$$\frac{{dz}}{{z}^{\mathrm{4}} }=\frac{{dt}}{\mathrm{3}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)+{t}\left({t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)} \\ $$$$.. \\ $$
