Menu Close

Solve-the-differential-equation-y-2ay-1-a-2-y-te-at-sint-

Tinku Tara 0 Comments
Pin




Question Number 105646 by Ar Brandon last updated on 30/Jul/20
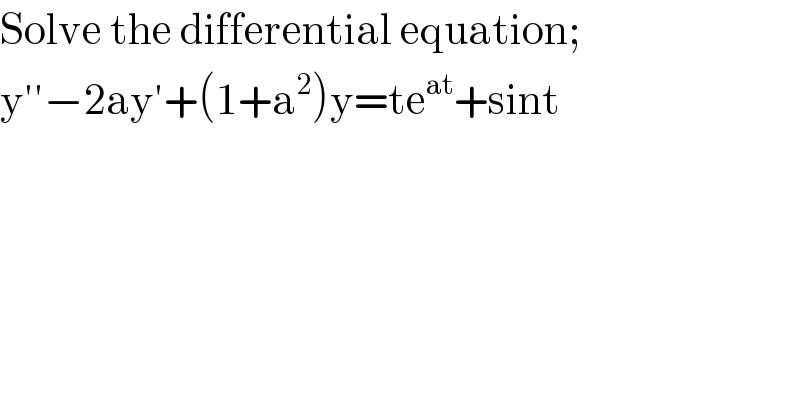
Solve the differential equation; y′′−2ay′+(1+a^2 )y=te^(at) +sint
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equation}; \\ $$$$\mathrm{y}''−\mathrm{2ay}'+\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)\mathrm{y}=\mathrm{te}^{\mathrm{at}} +\mathrm{sint} \\ $$
Answered by mathmax by abdo last updated on 30/Jul/20
y^((2)) −2ay^((1)) +(1+a^2 )y =te^(at) +sint h→r^2 −2ar+(1+a^2 )=0→Δ^′ =a^2 −(1+a^2 ) =−1 ⇒ r_1 =a+i and r_2 =a−i ⇒y_h =e^(ax) {αcosx +βsinx} =αu_(1 ) +βu_2 W(u_1 ,u_2 ) = determinant (((e^(ax) cosx e^(ax) sinx)),(((acosx−sinx)e^(ax) (cosx +asinx)e^(ax) ))) =(cos^2 x+asinx cosx)e^(ax) −(acosxsinx−sin^2 x)e^(ax) =e^(ax) ≠0 W_1 = determinant (((o e^(ax) sinx)),((xe^(ax) +sinx (cosx+asinx)e^(ax) ))) =−e^(ax) sinx(xe^(ax) +sinx) W_2 = determinant (((e^(ax) cosx 0)),(((acosx−sinx)e^(ax) xe^(ax) +sinx)))=e^(ax) cosx(xe^(ax) +sinx) v_1 =∫ (w_1 /w)dx =−∫ ((e^(ax) sinx(xe^(ax) +sinx))/e^(ax) )dx =−∫ (xe^(ax) sinx dx +sin^2 x)dx =−∫ xe^(ax) sinx dx +∫((1+cos(2x))/2)dx ∫xe^(ax) sinx dx =Im(∫ x e^(ax+ix) dx) and ∫ x e^((a+i)x) dx =(x/(a+i))e^((a+i)x) −∫ (1/(a+i))e^((a+i)x) dx =(1/(a+i)) x e^((a+i)x) −(1/((a+i)^2 )) e^((a+i)x) rest to extract im(...) v_2 =∫ (w_2 /w)dx =∫ ((e^(ax) cosx(xe^(ax) +sinx))/e^(ax) )dx =∫ x e^(ax) cosx dx +∫ cosx sinx dx ∫ cosx sinx dx =(1/2)∫ sin(2x)dx =−(1/4)cos(2x) ∫ x e^(ax) cosx dx =Re(∫ x e^((a+i)x) dx) ∫ x e^((a+i)x) dx =(x/(a+i))e^((a+i)x) −∫(1/(a+i))e^((a+i)x) dx =(((a−i)x)/(a^2 +1)) e^(ax) {cosx +isinx}−(((a−i)^2 )/((a^2 +1)^2 )) e^(ax) {cosx +isinx} rest to extract Re (...) ⇒y_p =u_1 v_1 +u_2 v_2 and general solution is y =y_h +y_p
$$\mathrm{y}^{\left(\mathrm{2}\right)} −\mathrm{2ay}^{\left(\mathrm{1}\right)} \:+\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)\mathrm{y}\:=\mathrm{te}^{\mathrm{at}} \:+\mathrm{sint} \\ $$$$\mathrm{h}\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{2ar}+\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)=\mathrm{0}\rightarrow\Delta^{'} \:=\mathrm{a}^{\mathrm{2}} −\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)\:=−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{r}_{\mathrm{1}} =\mathrm{a}+\mathrm{i}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\mathrm{a}−\mathrm{i}\:\Rightarrow\mathrm{y}_{\mathrm{h}} =\mathrm{e}^{\mathrm{ax}} \left\{\alpha\mathrm{cosx}\:+\beta\mathrm{sinx}\right\}\:=\alpha\mathrm{u}_{\mathrm{1}\:} \:+\beta\mathrm{u}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} \:,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{e}^{\mathrm{ax}} \mathrm{cosx}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{ax}} \mathrm{sinx}}\\{\left(\mathrm{acosx}−\mathrm{sinx}\right)\mathrm{e}^{\mathrm{ax}} \:\:\:\:\left(\mathrm{cosx}\:+\mathrm{asinx}\right)\mathrm{e}^{\mathrm{ax}} }\end{vmatrix} \\ $$$$=\left(\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{asinx}\:\mathrm{cosx}\right)\mathrm{e}^{\mathrm{ax}} −\left(\mathrm{acosxsinx}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)\mathrm{e}^{\mathrm{ax}} \:=\mathrm{e}^{\mathrm{ax}} \:\:\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{ax}} \mathrm{sinx}}\\{\mathrm{xe}^{\mathrm{ax}} \:+\mathrm{sinx}\:\:\:\:\:\left(\mathrm{cosx}+\mathrm{asinx}\right)\mathrm{e}^{\mathrm{ax}} }\end{vmatrix} \\ $$$$=−\mathrm{e}^{\mathrm{ax}} \mathrm{sinx}\left(\mathrm{xe}^{\mathrm{ax}} \:+\mathrm{sinx}\right) \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{ax}} \:\mathrm{cosx}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\left(\mathrm{acosx}−\mathrm{sinx}\right)\mathrm{e}^{\mathrm{ax}} \:\:\:\:\:\:\:\:\mathrm{xe}^{\mathrm{ax}} \:+\mathrm{sinx}}\end{vmatrix}=\mathrm{e}^{\mathrm{ax}} \mathrm{cosx}\left(\mathrm{xe}^{\mathrm{ax}} \:+\mathrm{sinx}\right) \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=−\int\:\frac{\mathrm{e}^{\mathrm{ax}} \mathrm{sinx}\left(\mathrm{xe}^{\mathrm{ax}} \:+\mathrm{sinx}\right)}{\mathrm{e}^{\mathrm{ax}} }\mathrm{dx} \\ $$$$=−\int\:\left(\mathrm{xe}^{\mathrm{ax}} \mathrm{sinx}\:\mathrm{dx}\:+\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dx}\:=−\int\:\mathrm{xe}^{\mathrm{ax}} \mathrm{sinx}\:\mathrm{dx}\:+\int\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}\mathrm{dx} \\ $$$$\int\mathrm{xe}^{\mathrm{ax}} \mathrm{sinx}\:\mathrm{dx}\:=\mathrm{Im}\left(\int\:\mathrm{x}\:\mathrm{e}^{\mathrm{ax}+\mathrm{ix}} \mathrm{dx}\right)\:\mathrm{and} \\ $$$$\int\:\mathrm{x}\:\mathrm{e}^{\left(\mathrm{a}+\mathrm{i}\right)\mathrm{x}} \mathrm{dx}\:=\frac{\mathrm{x}}{\mathrm{a}+\mathrm{i}}\mathrm{e}^{\left(\mathrm{a}+\mathrm{i}\right)\mathrm{x}} \:−\int\:\frac{\mathrm{1}}{\mathrm{a}+\mathrm{i}}\mathrm{e}^{\left(\mathrm{a}+\mathrm{i}\right)\mathrm{x}} \mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{a}+\mathrm{i}}\:\mathrm{x}\:\mathrm{e}^{\left(\mathrm{a}+\mathrm{i}\right)\mathrm{x}} −\frac{\mathrm{1}}{\left(\mathrm{a}+\mathrm{i}\right)^{\mathrm{2}} }\:\mathrm{e}^{\left(\mathrm{a}+\mathrm{i}\right)\mathrm{x}} \:\:\mathrm{rest}\:\mathrm{to}\:\mathrm{extract}\:\mathrm{im}\left(…\right) \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\frac{\mathrm{e}^{\mathrm{ax}} \mathrm{cosx}\left(\mathrm{xe}^{\mathrm{ax}} \:+\mathrm{sinx}\right)}{\mathrm{e}^{\mathrm{ax}} }\mathrm{dx} \\ $$$$=\int\:\:\mathrm{x}\:\mathrm{e}^{\mathrm{ax}} \:\mathrm{cosx}\:\mathrm{dx}\:+\int\:\mathrm{cosx}\:\mathrm{sinx}\:\mathrm{dx} \\ $$$$\int\:\mathrm{cosx}\:\mathrm{sinx}\:\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{sin}\left(\mathrm{2x}\right)\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\left(\mathrm{2x}\right) \\ $$$$\int\:\mathrm{x}\:\mathrm{e}^{\mathrm{ax}} \:\mathrm{cosx}\:\mathrm{dx}\:=\mathrm{Re}\left(\int\:\mathrm{x}\:\mathrm{e}^{\left(\mathrm{a}+\mathrm{i}\right)\mathrm{x}} \mathrm{dx}\right) \\ $$$$\int\:\mathrm{x}\:\mathrm{e}^{\left(\mathrm{a}+\mathrm{i}\right)\mathrm{x}} \mathrm{dx}\:=\frac{\mathrm{x}}{\mathrm{a}+\mathrm{i}}\mathrm{e}^{\left(\mathrm{a}+\mathrm{i}\right)\mathrm{x}} −\int\frac{\mathrm{1}}{\mathrm{a}+\mathrm{i}}\mathrm{e}^{\left(\mathrm{a}+\mathrm{i}\right)\mathrm{x}} \mathrm{dx} \\ $$$$=\frac{\left(\mathrm{a}−\mathrm{i}\right)\mathrm{x}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\:\mathrm{e}^{\mathrm{ax}} \left\{\mathrm{cosx}\:+\mathrm{isinx}\right\}−\frac{\left(\mathrm{a}−\mathrm{i}\right)^{\mathrm{2}} }{\left(\mathrm{a}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{e}^{\mathrm{ax}} \left\{\mathrm{cosx}\:+\mathrm{isinx}\right\} \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{extract}\:\mathrm{Re}\:\left(…\right)\:\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$
Commented by Ar Brandon last updated on 30/Jul/20
Thanks
Commented by mathmax by abdo last updated on 31/Jul/20
you are welcome
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *