Question Number 25572 by hoangnampham13 last updated on 11/Dec/17

$${Solve}\:{the}\:{differential}\:{equation}: \\ $$$${y}'\:=\:{cosh}\left({x}+{y}\right) \\ $$
Answered by prakash jain last updated on 11/Dec/17
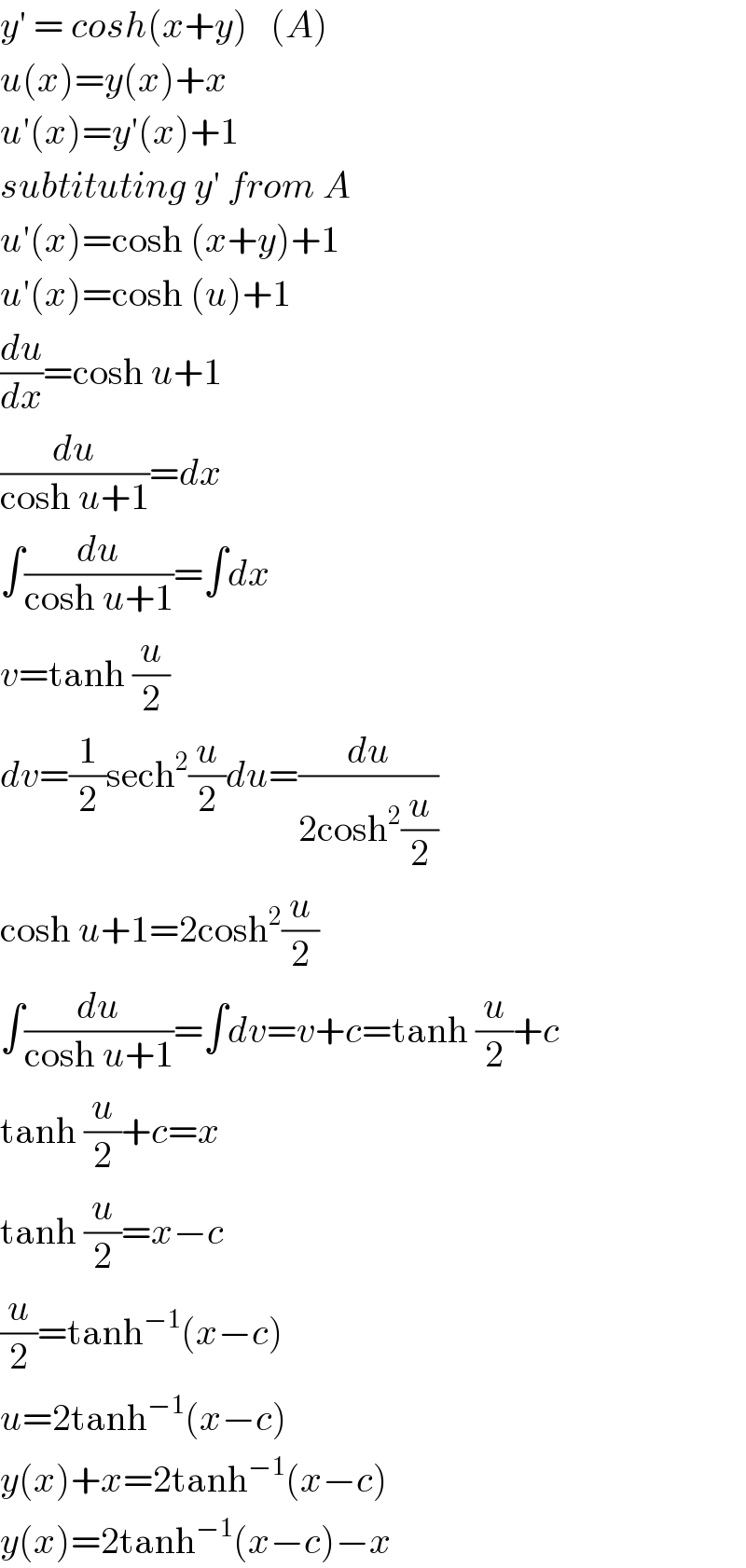
$${y}'\:=\:{cosh}\left({x}+{y}\right)\:\:\:\left({A}\right) \\ $$$${u}\left({x}\right)={y}\left({x}\right)+{x} \\ $$$${u}'\left({x}\right)={y}'\left({x}\right)+\mathrm{1} \\ $$$${subtituting}\:{y}'\:{from}\:{A} \\ $$$${u}'\left({x}\right)=\mathrm{cosh}\:\left({x}+{y}\right)+\mathrm{1} \\ $$$${u}'\left({x}\right)=\mathrm{cosh}\:\left({u}\right)+\mathrm{1} \\ $$$$\frac{{du}}{{dx}}=\mathrm{cosh}\:{u}+\mathrm{1} \\ $$$$\frac{{du}}{\mathrm{cosh}\:{u}+\mathrm{1}}={dx} \\ $$$$\int\frac{{du}}{\mathrm{cosh}\:{u}+\mathrm{1}}=\int{dx} \\ $$$${v}=\mathrm{tanh}\:\frac{{u}}{\mathrm{2}} \\ $$$${dv}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sech}^{\mathrm{2}} \frac{{u}}{\mathrm{2}}{du}=\frac{{du}}{\mathrm{2cosh}^{\mathrm{2}} \frac{{u}}{\mathrm{2}}} \\ $$$$\mathrm{cosh}\:{u}+\mathrm{1}=\mathrm{2cosh}^{\mathrm{2}} \frac{{u}}{\mathrm{2}} \\ $$$$\int\frac{{du}}{\mathrm{cosh}\:{u}+\mathrm{1}}=\int{dv}={v}+{c}=\mathrm{tanh}\:\frac{{u}}{\mathrm{2}}+{c} \\ $$$$\mathrm{tanh}\:\frac{{u}}{\mathrm{2}}+{c}={x} \\ $$$$\mathrm{tanh}\:\frac{{u}}{\mathrm{2}}={x}−{c} \\ $$$$\frac{{u}}{\mathrm{2}}=\mathrm{tanh}^{−\mathrm{1}} \left({x}−{c}\right) \\ $$$${u}=\mathrm{2tanh}^{−\mathrm{1}} \left({x}−{c}\right) \\ $$$${y}\left({x}\right)+{x}=\mathrm{2tanh}^{−\mathrm{1}} \left({x}−{c}\right) \\ $$$${y}\left({x}\right)=\mathrm{2tanh}^{−\mathrm{1}} \left({x}−{c}\right)−{x} \\ $$
