Question Number 100594 by Coronavirus last updated on 27/Jun/20
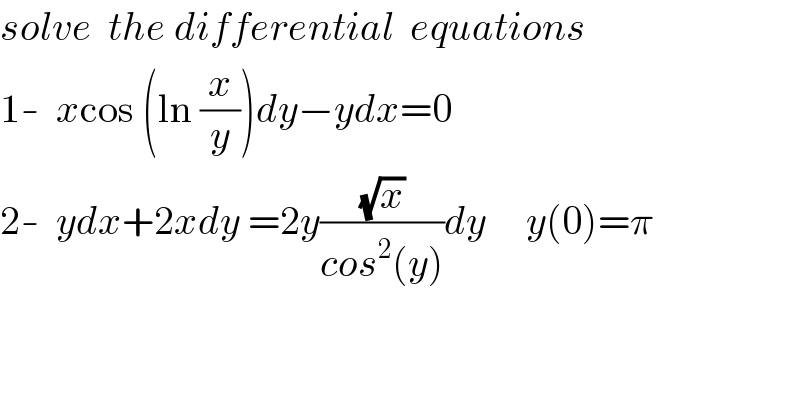
$${solve}\:\:{the}\:{differential}\:\:{equations} \\ $$$$\mathrm{1}-\:\:{x}\mathrm{cos}\:\left(\mathrm{ln}\:\frac{{x}}{{y}}\right){dy}−{ydx}=\mathrm{0} \\ $$$$\mathrm{2}-\:\:{ydx}+\mathrm{2}{xdy}\:=\mathrm{2}{y}\frac{\sqrt{{x}}}{{cos}^{\mathrm{2}} \left({y}\right)}{dy}\:\:\:\:\:{y}\left(\mathrm{0}\right)=\pi \\ $$
Answered by smridha last updated on 27/Jun/20
![2.[(dx/(2(√x)))+((√x)/y)dy=sec^2 (y)dy] mult: by y both sides and integrating ∫d(y.(√x))=∫y.sec^2 (y)dy ⇒y(√x)=ytan(y)+ln[cos(y)]+c put the condition y(0)=𝛑 ⇒0=0+ln(−1)+c so c=+_− i𝛑 so the solution y(√x)=ytan(y)+ln[cos(y)]+_− i𝛑](https://www.tinkutara.com/question/Q100619.png)
$$\mathrm{2}.\left[\frac{\boldsymbol{{dx}}}{\mathrm{2}\sqrt{\boldsymbol{{x}}}}+\frac{\sqrt{\boldsymbol{{x}}}}{\boldsymbol{{y}}}\boldsymbol{{dy}}=\boldsymbol{{sec}}^{\mathrm{2}} \left(\boldsymbol{{y}}\right)\boldsymbol{{dy}}\right] \\ $$$$\boldsymbol{{mult}}:\:\boldsymbol{{by}}\:\boldsymbol{{y}}\:\boldsymbol{{both}}\:\boldsymbol{{sides}}\:\boldsymbol{{and}}\:\boldsymbol{{integrating}} \\ $$$$\int\boldsymbol{{d}}\left(\boldsymbol{{y}}.\sqrt{\boldsymbol{{x}}}\right)=\int\boldsymbol{{y}}.\boldsymbol{{sec}}^{\mathrm{2}} \left(\boldsymbol{{y}}\right)\boldsymbol{{dy}} \\ $$$$\Rightarrow\boldsymbol{{y}}\sqrt{\boldsymbol{{x}}}=\boldsymbol{{ytan}}\left(\boldsymbol{{y}}\right)+\boldsymbol{{ln}}\left[\boldsymbol{{cos}}\left(\boldsymbol{{y}}\right)\right]+\boldsymbol{{c}} \\ $$$$\boldsymbol{{put}}\:\boldsymbol{{the}}\:\boldsymbol{{condition}}\:\boldsymbol{{y}}\left(\mathrm{0}\right)=\boldsymbol{\pi} \\ $$$$\Rightarrow\mathrm{0}=\mathrm{0}+\boldsymbol{{ln}}\left(−\mathrm{1}\right)+\boldsymbol{{c}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{c}}=\underset{−} {+}\boldsymbol{{i}\pi} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{the}}\:\boldsymbol{{solution}}\: \\ $$$$\boldsymbol{{y}}\sqrt{\boldsymbol{{x}}}=\boldsymbol{{ytan}}\left(\boldsymbol{{y}}\right)+\boldsymbol{{ln}}\left[\boldsymbol{{cos}}\left(\boldsymbol{{y}}\right)\right]\underset{−} {+}\boldsymbol{{i}\pi} \\ $$
Answered by smridha last updated on 28/Jun/20
![(1).(dx/dy)=(x/(2y))[((x/y))^i +((x/y))^(−i) ] let (x/y)=v so (dx/dy)=v+y.(dv/dy) now v+y.(dv/dy)=(v/2)[((v^(2i) +1)/v^i )] y.(dv/dy)=v[(((v^i −1)^2 )/(2v^i ))] (dy/y)=((2v^(i−1) )/((v^i −1)^2 ))dv integrating both sides we get.. ln(y)=2i.(1/((v^i −1)))+ln(c) so y=c.e^((2i)/([((x/y))^i −1]))](https://www.tinkutara.com/question/Q100688.png)
$$\left(\mathrm{1}\right).\frac{\boldsymbol{{dx}}}{\boldsymbol{{dy}}}=\frac{\boldsymbol{{x}}}{\mathrm{2}\boldsymbol{{y}}}\left[\left(\frac{\boldsymbol{{x}}}{\boldsymbol{{y}}}\right)^{\boldsymbol{{i}}} +\left(\frac{\boldsymbol{{x}}}{\boldsymbol{{y}}}\right)^{−\boldsymbol{{i}}} \right] \\ $$$$\boldsymbol{{let}}\:\:\:\frac{\boldsymbol{{x}}}{\boldsymbol{{y}}}=\boldsymbol{{v}}\:\boldsymbol{{so}}\:\frac{\boldsymbol{{dx}}}{\boldsymbol{{dy}}}=\boldsymbol{{v}}+\boldsymbol{{y}}.\frac{\boldsymbol{{dv}}}{\boldsymbol{{dy}}} \\ $$$$\boldsymbol{{now}}\: \\ $$$$\:\:\:\boldsymbol{{v}}+\boldsymbol{{y}}.\frac{\boldsymbol{{dv}}}{\boldsymbol{{dy}}}=\frac{\boldsymbol{{v}}}{\mathrm{2}}\left[\frac{\boldsymbol{{v}}^{\mathrm{2}\boldsymbol{{i}}} +\mathrm{1}}{\boldsymbol{{v}}^{\boldsymbol{{i}}} }\right] \\ $$$$\boldsymbol{{y}}.\frac{\boldsymbol{{dv}}}{\boldsymbol{{dy}}}=\boldsymbol{{v}}\left[\frac{\left(\boldsymbol{{v}}^{\boldsymbol{{i}}} −\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}\boldsymbol{{v}}^{\boldsymbol{{i}}} }\right] \\ $$$$\frac{\boldsymbol{{dy}}}{\boldsymbol{{y}}}=\frac{\mathrm{2}\boldsymbol{{v}}^{\boldsymbol{{i}}−\mathrm{1}} }{\left(\boldsymbol{{v}}^{\boldsymbol{{i}}} −\mathrm{1}\right)^{\mathrm{2}} }\boldsymbol{{dv}} \\ $$$$\boldsymbol{{integrating}}\:\boldsymbol{{both}}\:\boldsymbol{{sides}}\:\boldsymbol{{we}}\:\boldsymbol{{get}}.. \\ $$$$\boldsymbol{{ln}}\left(\boldsymbol{{y}}\right)=\mathrm{2}\boldsymbol{{i}}.\frac{\mathrm{1}}{\left(\boldsymbol{{v}}^{\boldsymbol{{i}}} −\mathrm{1}\right)}+\boldsymbol{{ln}}\left(\boldsymbol{{c}}\right) \\ $$$$\boldsymbol{{so}}\:\:\:\boldsymbol{{y}}=\boldsymbol{{c}}.\boldsymbol{{e}}^{\frac{\mathrm{2}\boldsymbol{{i}}}{\left[\left(\frac{\boldsymbol{{x}}}{\boldsymbol{{y}}}\right)^{\boldsymbol{{i}}} −\mathrm{1}\right]}} \\ $$
