Question Number 89908 by I want to learn more last updated on 19/Apr/20
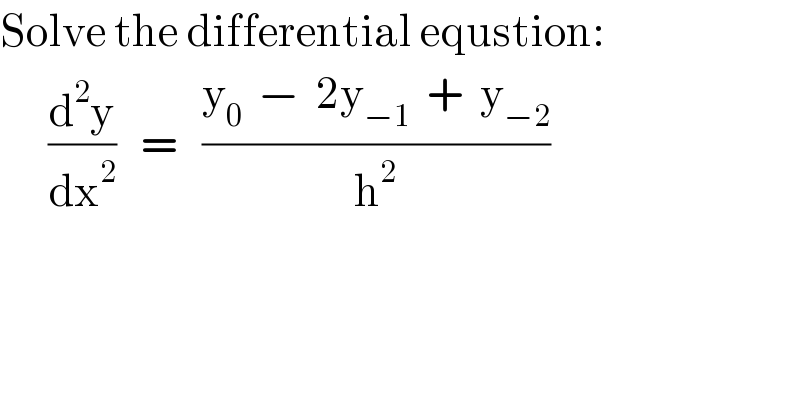
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equstion}: \\ $$$$\:\:\:\:\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:\:\:=\:\:\:\frac{\mathrm{y}_{\mathrm{0}} \:\:−\:\:\mathrm{2y}_{−\mathrm{1}} \:\:+\:\:\mathrm{y}_{−\mathrm{2}} }{\mathrm{h}^{\mathrm{2}} } \\ $$
Commented by I want to learn more last updated on 19/Apr/20
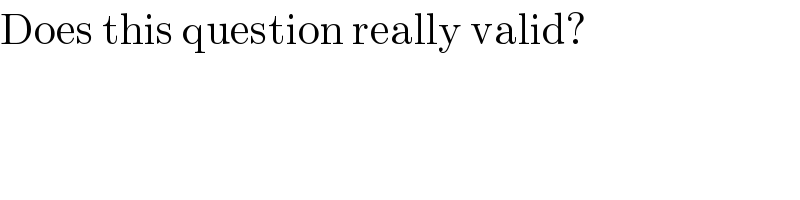
$$\mathrm{Does}\:\mathrm{this}\:\mathrm{question}\:\mathrm{really}\:\mathrm{valid}? \\ $$
Commented by MJS last updated on 20/Apr/20
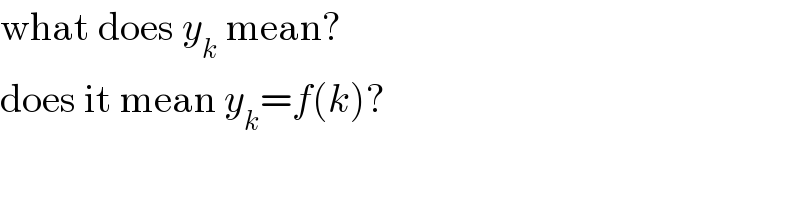
$$\mathrm{what}\:\mathrm{does}\:{y}_{{k}} \:\mathrm{mean}? \\ $$$$\mathrm{does}\:\mathrm{it}\:\mathrm{mean}\:{y}_{{k}} ={f}\left({k}\right)? \\ $$
Commented by I want to learn more last updated on 20/Apr/20

$$\mathrm{Yes}\:\mathrm{sir} \\ $$
Commented by I want to learn more last updated on 20/Apr/20

$$\mathrm{Please}\:\mathrm{help}\:\mathrm{me} \\ $$
Commented by mr W last updated on 20/Apr/20
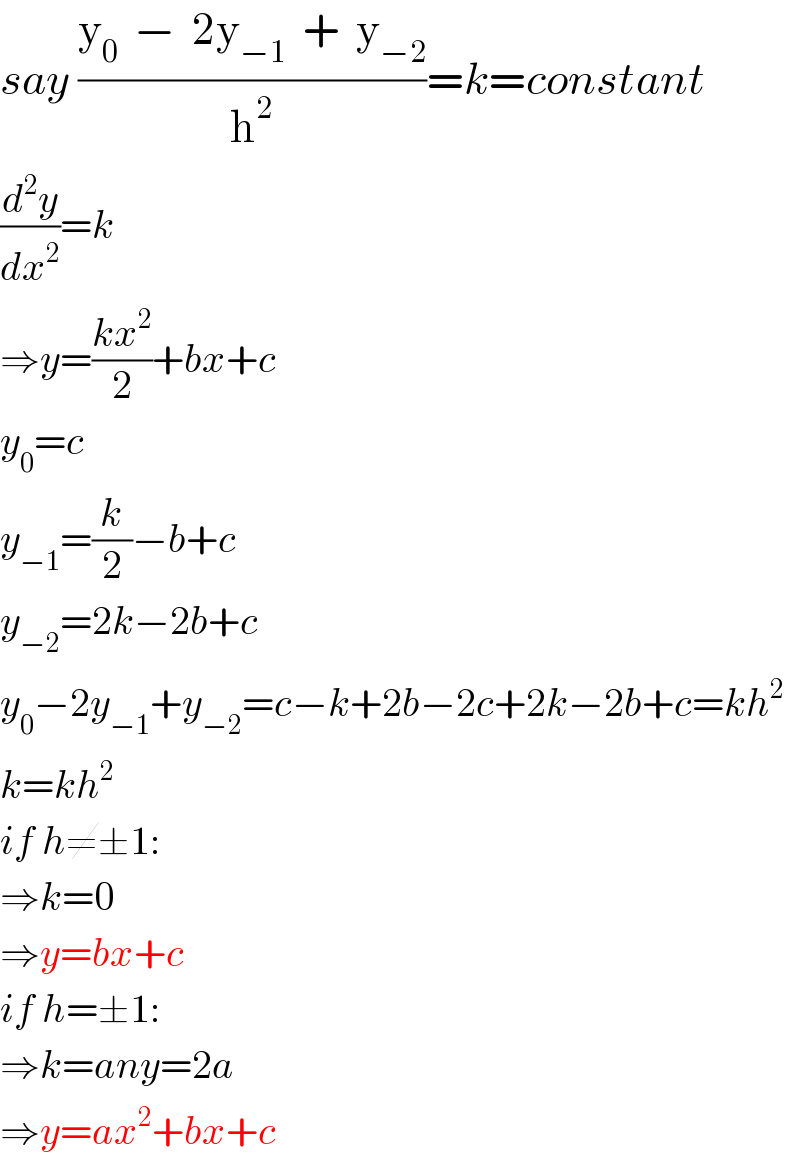
$${say}\:\frac{\mathrm{y}_{\mathrm{0}} \:\:−\:\:\mathrm{2y}_{−\mathrm{1}} \:\:+\:\:\mathrm{y}_{−\mathrm{2}} }{\mathrm{h}^{\mathrm{2}} }={k}={constant} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }={k} \\ $$$$\Rightarrow{y}=\frac{{kx}^{\mathrm{2}} }{\mathrm{2}}+{bx}+{c} \\ $$$${y}_{\mathrm{0}} ={c} \\ $$$${y}_{−\mathrm{1}} =\frac{{k}}{\mathrm{2}}−{b}+{c} \\ $$$${y}_{−\mathrm{2}} =\mathrm{2}{k}−\mathrm{2}{b}+{c} \\ $$$${y}_{\mathrm{0}} −\mathrm{2}{y}_{−\mathrm{1}} +{y}_{−\mathrm{2}} ={c}−{k}+\mathrm{2}{b}−\mathrm{2}{c}+\mathrm{2}{k}−\mathrm{2}{b}+{c}={kh}^{\mathrm{2}} \\ $$$${k}={kh}^{\mathrm{2}} \\ $$$${if}\:{h}\neq\pm\mathrm{1}: \\ $$$$\Rightarrow{k}=\mathrm{0} \\ $$$$\Rightarrow{y}={bx}+{c} \\ $$$${if}\:{h}=\pm\mathrm{1}: \\ $$$$\Rightarrow{k}={any}=\mathrm{2}{a} \\ $$$$\Rightarrow{y}={ax}^{\mathrm{2}} +{bx}+{c} \\ $$
Commented by I want to learn more last updated on 20/Apr/20
$$\mathrm{Wow},\:\:\mathrm{i}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
