Question Number 27782 by abdo imad last updated on 14/Jan/18
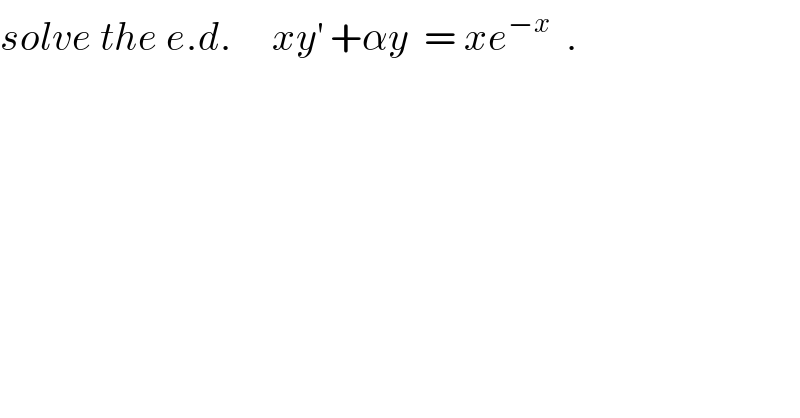
$${solve}\:{the}\:{e}.{d}.\:\:\:\:\:{xy}^{'} \:+\alpha{y}\:\:=\:{xe}^{−{x}} \:\:. \\ $$
Commented by abdo imad last updated on 18/Jan/18

$${if}\:\alpha=\mathrm{0}\:\:\:\:{e}\:\:\Leftrightarrow\:\:{xy}^{'} =\:{x}\:{e}^{−{x}} \Rightarrow\:{y}^{'} \:=\:{e}^{−{x}} \:\Rightarrow{y}=\:\int\:{e}^{−{x}} {dx}\:+{k} \\ $$$${y}=\:−{e}^{−{x}} +{k} \\ $$$${if}\:\alpha\neq\mathrm{0}\:\:\:{h}.{e}\:\:\:\:\:\:\:\:\:\:{xy}^{'} \:+\alpha{y}=\mathrm{0}\:\Leftrightarrow\:\frac{{y}^{'} }{{y}}=\frac{−\alpha}{{x}}\:\:\Rightarrow{ln}/{y}/=−\alpha\:{ln}/{x}/+{k} \\ $$$$\Rightarrow\:{y}=\:\:\frac{\lambda}{/{x}/^{\alpha} }\:\:\:\left({x}\neq\mathrm{0}\right)\: \\ $$$${case}\:\mathrm{1}\:\:\:\:\:\:\:\:\:{x}>\mathrm{0}\:\:\Rightarrow\:{y}\:=\:\frac{\lambda}{{x}^{\alpha} }\:\:{let}\:{use}\:{m}.{v}.{c}\:{mehod} \\ $$$${y}^{'} =\:\lambda^{'} \:{x}^{−\alpha} \:\:−\alpha\:\lambda\:{x}^{−\alpha−\mathrm{1}} \\ $$$$\left({e}\right)\:\Leftrightarrow\:\:\:\lambda^{'} \:{x}^{\mathrm{1}−\alpha} \:−\alpha\lambda\:{x}^{−\alpha} \:+\alpha\lambda\:{x}^{−\alpha} \:\:={x}\:{e}^{−{x}} \\ $$$$\Leftrightarrow\:\:\lambda^{'} =\:\:\frac{{x}}{{x}^{\mathrm{1}−\alpha} }\:{e}^{−{x}} \:\:=\:{x}^{\alpha} \:{e}^{−{x}} \:\Rightarrow\:\lambda\:=\:\int\:{x}^{\alpha} \:{e}^{−{x}} {dx}\:+{c} \\ $$$${y}=\:\:\frac{\int\:{x}^{\alpha} \:{e}^{−{x}} {dx}\:+{c}}{{x}^{\alpha} } \\ $$$${case}\:\mathrm{2}\:\:\:\:{if}\:\:{x}<\mathrm{0}\:\:{we}\:{folow}\:{the}\:{same}\:{method}\:{to}\:{find}\:{the}\:{solution}. \\ $$$$ \\ $$
