Menu Close

solve-the-eqn-dr-d-r-a-2-r-2-a-2-r-2-cot-hint-let-a-2-r-2-a-2-r-2-2r-2-

Tinku Tara 0 Comments
Pin




Question Number 14630 by Don sai last updated on 03/Jun/17
solve the eqn dr/dθ=[r(a^2 −r^2 )/a^2 +r^2 ]cotθ hint. let a^2 +r^2 =a^2 −r^2 +2r^2 .
$$\mathrm{solve}\:\mathrm{the}\:\mathrm{eqn} \\ $$$$\mathrm{dr}/\mathrm{d}\theta=\left[\mathrm{r}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{r}^{\mathrm{2}} \right)/\mathrm{a}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} \right]\mathrm{cot}\theta \\ $$$$\mathrm{hint}.\:\mathrm{let}\:\mathrm{a}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} −\mathrm{r}^{\mathrm{2}} +\mathrm{2r}^{\mathrm{2}} . \\ $$
Commented by prakash jain last updated on 03/Jun/17
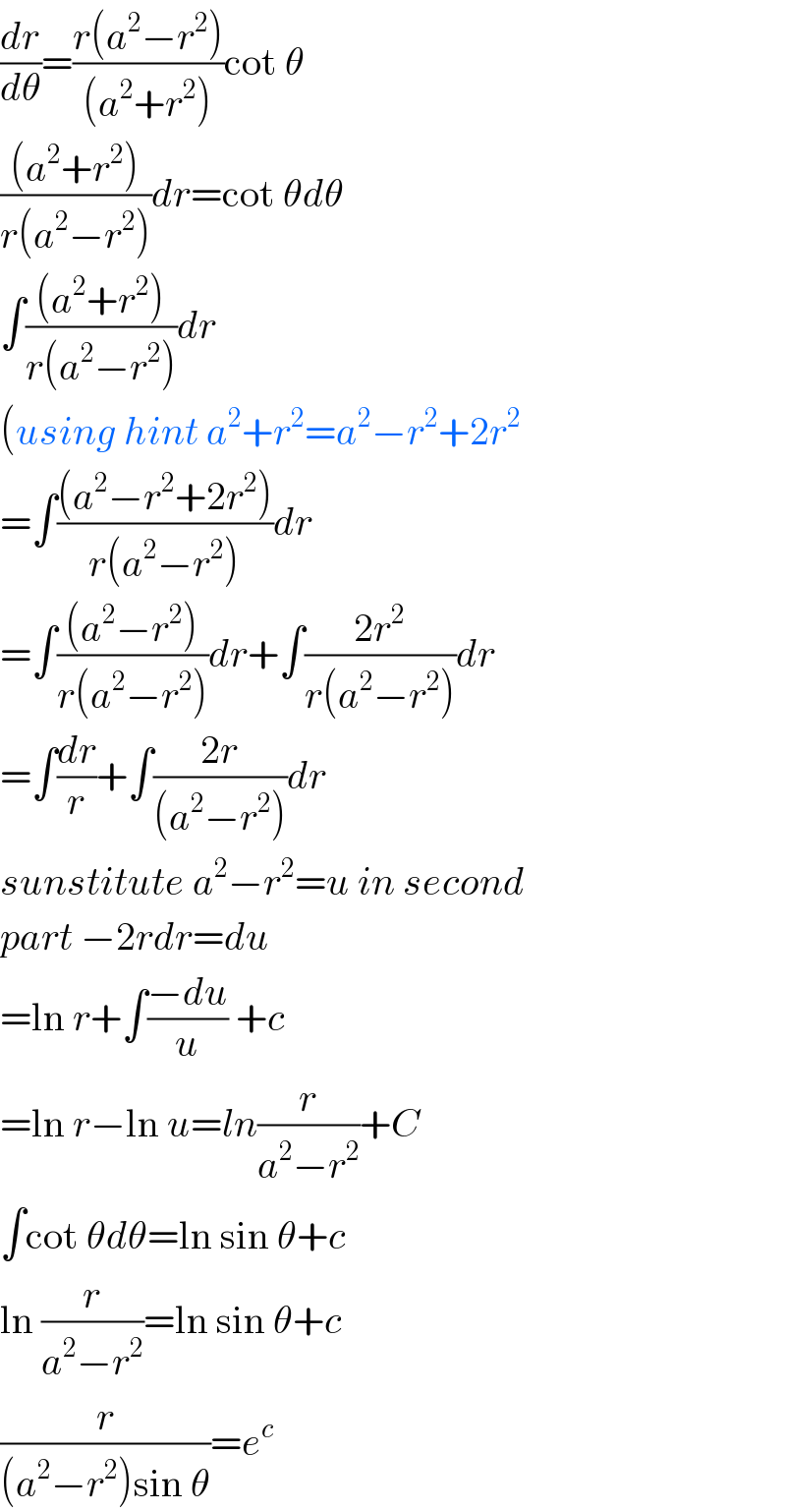
(dr/dθ)=((r(a^2 −r^2 ))/((a^2 +r^2 )))cot θ (((a^2 +r^2 ))/(r(a^2 −r^2 )))dr=cot θdθ ∫(((a^2 +r^2 ))/(r(a^2 −r^2 )))dr (using hint a^2 +r^2 =a^2 −r^2 +2r^2 =∫(((a^2 −r^2 +2r^2 ))/(r(a^2 −r^2 )))dr =∫(((a^2 −r^2 ))/(r(a^2 −r^2 )))dr+∫((2r^2 )/(r(a^2 −r^2 )))dr =∫(dr/r)+∫((2r)/((a^2 −r^2 )))dr sunstitute a^2 −r^2 =u in second part −2rdr=du =ln r+∫((−du)/u) +c =ln r−ln u=ln(r/(a^2 −r^2 ))+C ∫cot θdθ=ln sin θ+c ln (r/(a^2 −r^2 ))=ln sin θ+c (r/((a^2 −r^2 )sin θ))=e^c
$$\frac{{dr}}{{d}\theta}=\frac{{r}\left({a}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)}{\left({a}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)}\mathrm{cot}\:\theta \\ $$$$\frac{\left({a}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)}{{r}\left({a}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)}{dr}=\mathrm{cot}\:\theta{d}\theta \\ $$$$\int\frac{\left({a}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)}{{r}\left({a}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)}{dr} \\ $$$$\left({using}\:{hint}\:{a}^{\mathrm{2}} +{r}^{\mathrm{2}} ={a}^{\mathrm{2}} −{r}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{2}} \right. \\ $$$$=\int\frac{\left({a}^{\mathrm{2}} −{r}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{2}} \right)}{{r}\left({a}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)}{dr} \\ $$$$=\int\frac{\left({a}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)}{{r}\left({a}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)}{dr}+\int\frac{\mathrm{2}{r}^{\mathrm{2}} }{{r}\left({a}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)}{dr} \\ $$$$=\int\frac{{dr}}{{r}}+\int\frac{\mathrm{2}{r}}{\left({a}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)}{dr} \\ $$$${sunstitute}\:{a}^{\mathrm{2}} −{r}^{\mathrm{2}} ={u}\:{in}\:{second} \\ $$$${part}\:−\mathrm{2}{rdr}={du} \\ $$$$=\mathrm{ln}\:{r}+\int\frac{−{du}}{{u}}\:+{c} \\ $$$$=\mathrm{ln}\:{r}−\mathrm{ln}\:{u}={ln}\frac{{r}}{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }+{C} \\ $$$$\int\mathrm{cot}\:\theta{d}\theta=\mathrm{ln}\:\mathrm{sin}\:\theta+{c} \\ $$$$\mathrm{ln}\:\frac{{r}}{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }=\mathrm{ln}\:\mathrm{sin}\:\theta+{c} \\ $$$$\frac{{r}}{\left({a}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)\mathrm{sin}\:\theta}={e}^{{c}} \\ $$
Commented by Don sai last updated on 06/Jun/17
Thank you
$$\mathrm{Thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *