Question Number 14633 by Tinkutara last updated on 03/Jun/17
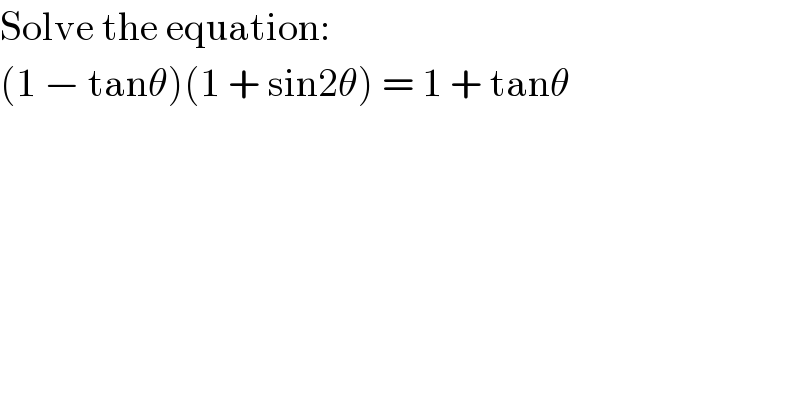
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}: \\ $$$$\left(\mathrm{1}\:−\:\mathrm{tan}\theta\right)\left(\mathrm{1}\:+\:\mathrm{sin2}\theta\right)\:=\:\mathrm{1}\:+\:\mathrm{tan}\theta \\ $$
Commented by myintkhaing last updated on 03/Jun/17
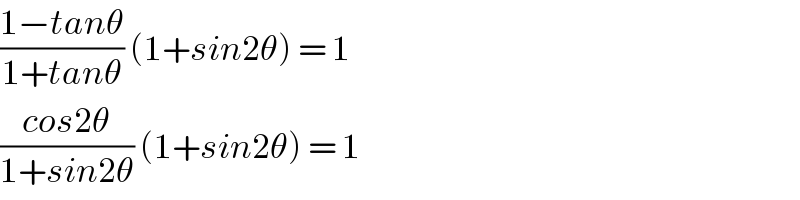
$$\frac{\mathrm{1}−{tan}\theta}{\mathrm{1}+{tan}\theta}\:\left(\mathrm{1}+{sin}\mathrm{2}\theta\right)\:=\:\mathrm{1} \\ $$$$\frac{{cos}\mathrm{2}\theta}{\mathrm{1}+{sin}\mathrm{2}\theta}\:\left(\mathrm{1}+{sin}\mathrm{2}\theta\right)\:=\:\mathrm{1} \\ $$
Answered by ajfour last updated on 03/Jun/17
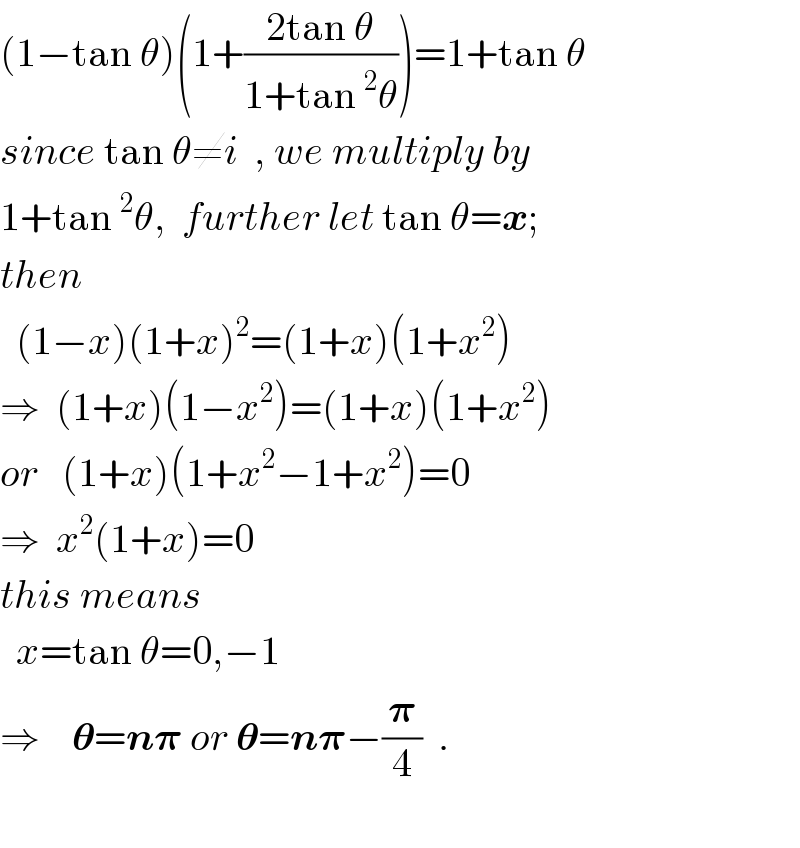
$$\left(\mathrm{1}−\mathrm{tan}\:\theta\right)\left(\mathrm{1}+\frac{\mathrm{2tan}\:\theta}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta}\right)=\mathrm{1}+\mathrm{tan}\:\theta \\ $$$${since}\:\mathrm{tan}\:\theta\neq{i}\:\:,\:{we}\:{multiply}\:{by} \\ $$$$\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta,\:\:{further}\:{let}\:\mathrm{tan}\:\theta=\boldsymbol{{x}}; \\ $$$${then} \\ $$$$\:\:\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}\right)^{\mathrm{2}} =\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\:\left(\mathrm{1}+{x}\right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right)=\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right) \\ $$$${or}\:\:\:\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{1}+{x}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)=\mathrm{0} \\ $$$${this}\:{means} \\ $$$$\:\:{x}=\mathrm{tan}\:\theta=\mathrm{0},−\mathrm{1} \\ $$$$\Rightarrow\:\:\:\:\boldsymbol{\theta}=\boldsymbol{{n}\pi}\:{or}\:\boldsymbol{\theta}=\boldsymbol{{n}\pi}−\frac{\boldsymbol{\pi}}{\mathrm{4}}\:\:. \\ $$$$ \\ $$
Commented by ajfour last updated on 03/Jun/17
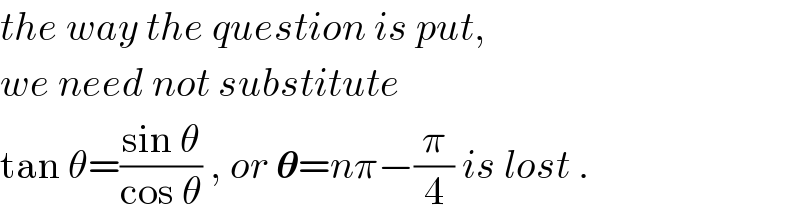
$${the}\:{way}\:{the}\:{question}\:{is}\:{put}, \\ $$$${we}\:{need}\:{not}\:{substitute}\: \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}\:,\:{or}\:\boldsymbol{\theta}={n}\pi−\frac{\pi}{\mathrm{4}}\:{is}\:{lost}\:. \\ $$
Commented by Tinkutara last updated on 03/Jun/17
$$\mathrm{Thanks}\:\mathrm{Sir}\:\mathrm{for}\:\mathrm{the}\:\mathrm{exact}\:\mathrm{solution}! \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 03/Jun/17
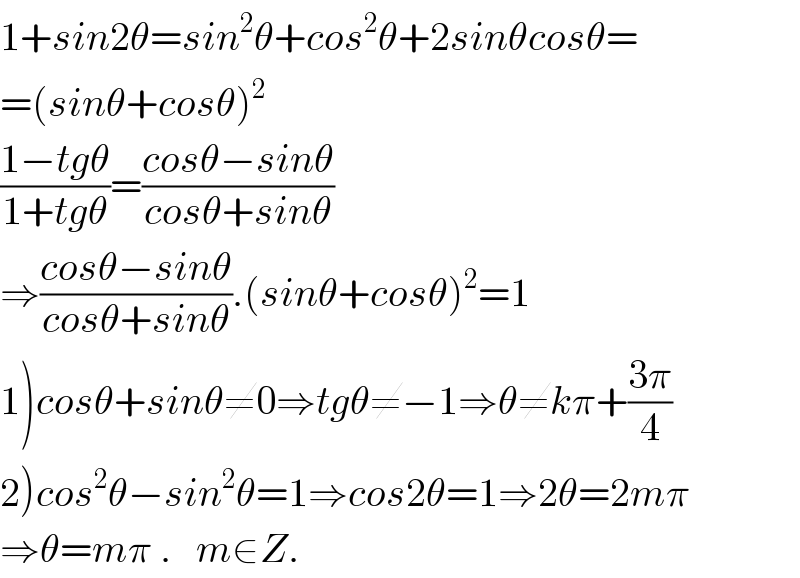
$$\mathrm{1}+{sin}\mathrm{2}\theta={sin}^{\mathrm{2}} \theta+{cos}^{\mathrm{2}} \theta+\mathrm{2}{sin}\theta{cos}\theta= \\ $$$$=\left({sin}\theta+{cos}\theta\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}−{tg}\theta}{\mathrm{1}+{tg}\theta}=\frac{{cos}\theta−{sin}\theta}{{cos}\theta+{sin}\theta} \\ $$$$\Rightarrow\frac{{cos}\theta−{sin}\theta}{{cos}\theta+{sin}\theta}.\left({sin}\theta+{cos}\theta\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\left.\mathrm{1}\right){cos}\theta+{sin}\theta\neq\mathrm{0}\Rightarrow{tg}\theta\neq−\mathrm{1}\Rightarrow\theta\neq{k}\pi+\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$$\left.\mathrm{2}\right){cos}^{\mathrm{2}} \theta−{sin}^{\mathrm{2}} \theta=\mathrm{1}\Rightarrow{cos}\mathrm{2}\theta=\mathrm{1}\Rightarrow\mathrm{2}\theta=\mathrm{2}{m}\pi \\ $$$$\Rightarrow\theta={m}\pi\:.\:\:\:{m}\in{Z}. \\ $$
Commented by Tinkutara last updated on 03/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
Answered by 1kanika# last updated on 03/Jun/17
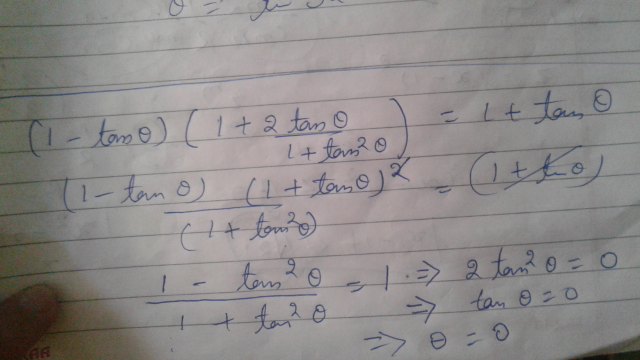
Commented by 1kanika# last updated on 03/Jun/17
$$\mathrm{sorry}…..\: \\ $$$$\:\theta=\mathrm{n}\pi\:\:\: \\ $$$${where}\:\:{n}\:\mathrm{belongs}\:\mathrm{to}\:\:\mathrm{Z} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 03/Jun/17
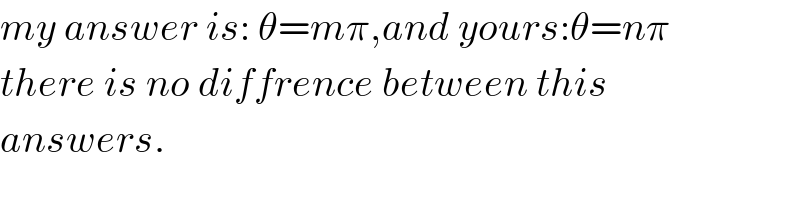
$${my}\:{answer}\:{is}:\:\theta={m}\pi,{and}\:{yours}:\theta={n}\pi \\ $$$${there}\:{is}\:{no}\:{diffrence}\:{between}\:{this}\: \\ $$$${answers}. \\ $$
Commented by Tinkutara last updated on 03/Jun/17
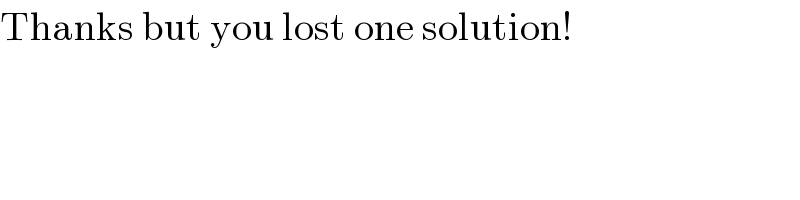
$$\mathrm{Thanks}\:\mathrm{but}\:\mathrm{you}\:\mathrm{lost}\:\mathrm{one}\:\mathrm{solution}! \\ $$
