Menu Close

Solve-the-equation-15-4-1-x-4-1-x-32-

Tinku Tara 0 Comments
Pin




Question Number 17271 by VEGAMIND last updated on 03/Jul/17
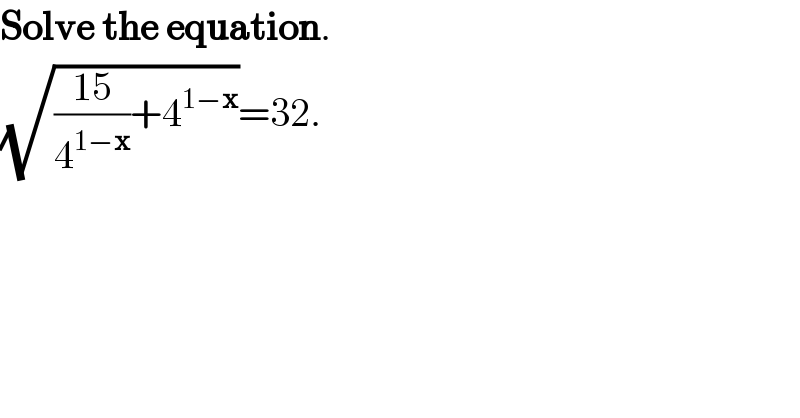
Solve the equation. (√(((15)/4^(1−x) )+4^(1−x) ))=32.
$$\boldsymbol{\mathrm{Solve}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{equation}}. \\ $$$$\sqrt{\frac{\mathrm{15}}{\mathrm{4}^{\mathrm{1}−\boldsymbol{\mathrm{x}}} }+\mathrm{4}^{\mathrm{1}−\boldsymbol{\mathrm{x}}} }=\mathrm{32}. \\ $$
Answered by RasheedSoomro last updated on 03/Jul/17
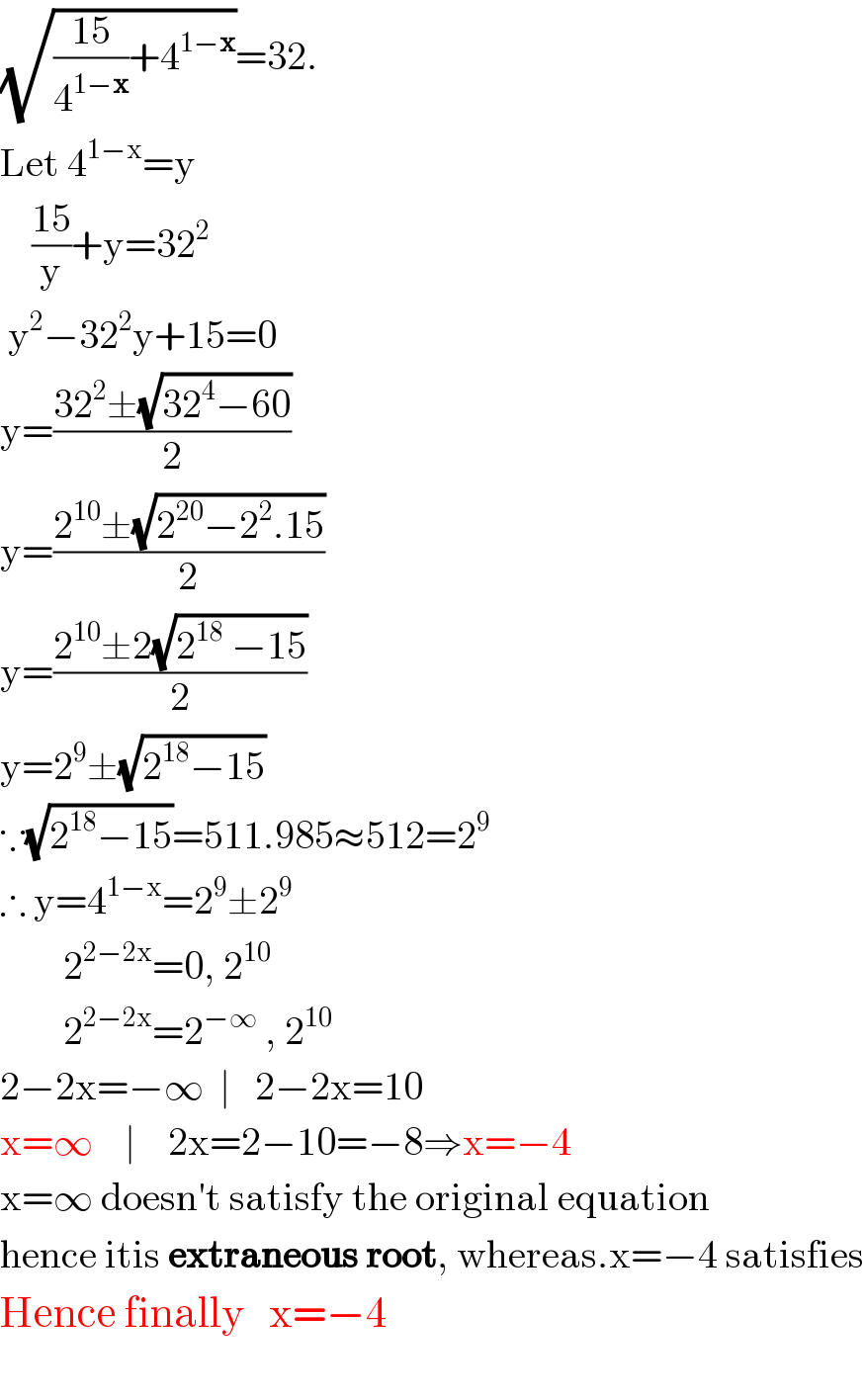
(√(((15)/4^(1−x) )+4^(1−x) ))=32. Let 4^(1−x) =y ((15)/y)+y=32^2 y^2 −32^2 y+15=0 y=((32^2 ±(√(32^4 −60)))/2) y=((2^(10) ±(√(2^(20) −2^2 .15)))/2) y=((2^(10) ±2(√(2^(18) −15)))/2) y=2^9 ±(√(2^(18) −15)) ∵(√(2^(18) −15))=511.985≈512=2^9 ∴ y=4^(1−x) =2^9 ±2^9 2^(2−2x) =0, 2^(10) 2^(2−2x) =2^(−∞) , 2^(10) 2−2x=−∞ ∣ 2−2x=10 x=∞ ∣ 2x=2−10=−8⇒x=−4 x=∞ doesn′t satisfy the original equation hence itis extraneous root, whereas.x=−4 satisfies Hence finally x=−4
$$\sqrt{\frac{\mathrm{15}}{\mathrm{4}^{\mathrm{1}−\boldsymbol{\mathrm{x}}} }+\mathrm{4}^{\mathrm{1}−\boldsymbol{\mathrm{x}}} }=\mathrm{32}. \\ $$$$\mathrm{Let}\:\mathrm{4}^{\mathrm{1}−\mathrm{x}} =\mathrm{y} \\ $$$$\:\:\:\:\frac{\mathrm{15}}{\mathrm{y}}+\mathrm{y}=\mathrm{32}^{\mathrm{2}} \\ $$$$\:\mathrm{y}^{\mathrm{2}} −\mathrm{32}^{\mathrm{2}} \mathrm{y}+\mathrm{15}=\mathrm{0} \\ $$$$\mathrm{y}=\frac{\mathrm{32}^{\mathrm{2}} \pm\sqrt{\mathrm{32}^{\mathrm{4}} −\mathrm{60}}}{\mathrm{2}} \\ $$$$\mathrm{y}=\frac{\mathrm{2}^{\mathrm{10}} \pm\sqrt{\mathrm{2}^{\mathrm{20}} −\mathrm{2}^{\mathrm{2}} .\mathrm{15}}}{\mathrm{2}} \\ $$$$\mathrm{y}=\frac{\mathrm{2}^{\mathrm{10}} \pm\mathrm{2}\sqrt{\mathrm{2}^{\mathrm{18}} \:−\mathrm{15}}}{\mathrm{2}} \\ $$$$\mathrm{y}=\mathrm{2}^{\mathrm{9}} \pm\sqrt{\mathrm{2}^{\mathrm{18}} −\mathrm{15}} \\ $$$$\because\sqrt{\mathrm{2}^{\mathrm{18}} −\mathrm{15}}=\mathrm{511}.\mathrm{985}\approx\mathrm{512}=\mathrm{2}^{\mathrm{9}} \\ $$$$\therefore\:\mathrm{y}=\mathrm{4}^{\mathrm{1}−\mathrm{x}} =\mathrm{2}^{\mathrm{9}} \pm\mathrm{2}^{\mathrm{9}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}^{\mathrm{2}−\mathrm{2x}} =\mathrm{0},\:\mathrm{2}^{\mathrm{10}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}^{\mathrm{2}−\mathrm{2x}} =\mathrm{2}^{−\infty} \:,\:\mathrm{2}^{\mathrm{10}} \\ $$$$\mathrm{2}−\mathrm{2x}=−\infty\:\:\mid\:\:\:\mathrm{2}−\mathrm{2x}=\mathrm{10} \\ $$$$\mathrm{x}=\infty\:\:\:\:\mid\:\:\:\:\mathrm{2x}=\mathrm{2}−\mathrm{10}=−\mathrm{8}\Rightarrow\mathrm{x}=−\mathrm{4} \\ $$$$\mathrm{x}=\infty\:\mathrm{doesn}'\mathrm{t}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{original}\:\mathrm{equation} \\ $$$$\mathrm{hence}\:\mathrm{itis}\:\boldsymbol{\mathrm{extraneous}}\:\boldsymbol{\mathrm{root}},\:\mathrm{whereas}.\mathrm{x}=−\mathrm{4}\:\mathrm{satisfies} \\ $$$$\mathrm{Hence}\:\mathrm{finally}\:\:\:\mathrm{x}=−\mathrm{4}\:\:\:\:\:\: \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *