Question Number 23445 by tawa tawa last updated on 30/Oct/17
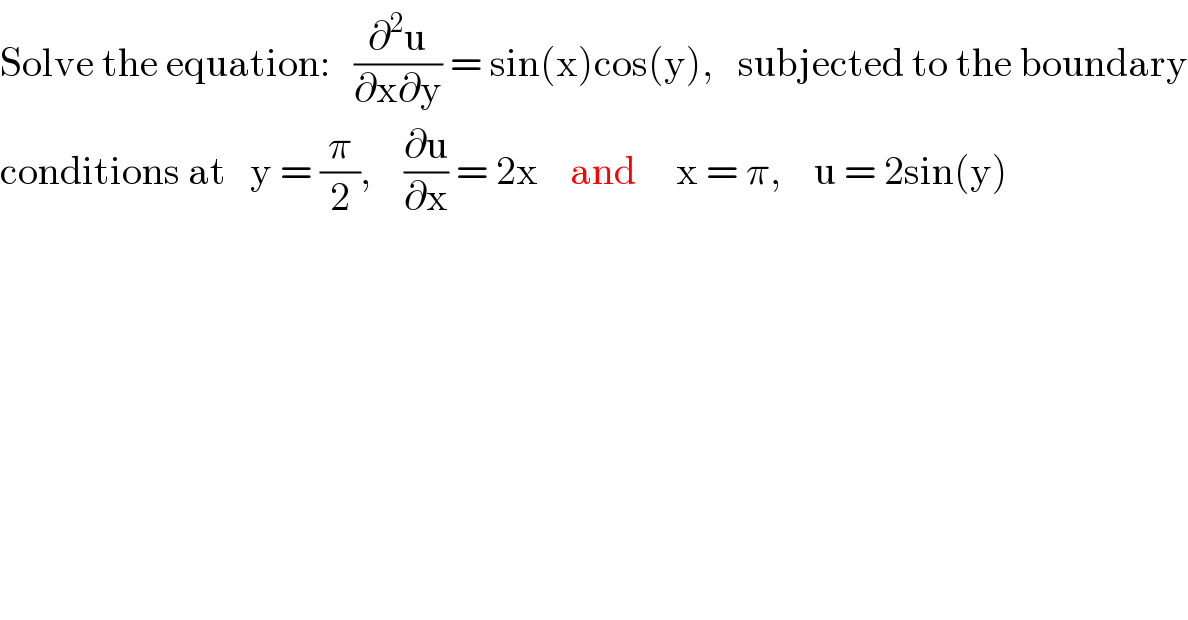
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}:\:\:\:\frac{\partial^{\mathrm{2}} \mathrm{u}}{\partial\mathrm{x}\partial\mathrm{y}}\:=\:\mathrm{sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{y}\right),\:\:\:\mathrm{subjected}\:\mathrm{to}\:\mathrm{the}\:\mathrm{boundary} \\ $$$$\mathrm{conditions}\:\mathrm{at}\:\:\:\mathrm{y}\:=\:\frac{\pi}{\mathrm{2}},\:\:\:\:\frac{\partial\mathrm{u}}{\partial\mathrm{x}}\:=\:\mathrm{2x}\:\:\:\:\mathrm{and}\:\:\:\:\:\mathrm{x}\:=\:\pi,\:\:\:\:\mathrm{u}\:=\:\mathrm{2sin}\left(\mathrm{y}\right) \\ $$
Answered by mrW1 last updated on 31/Oct/17
![(∂^2 u/(∂x∂y)) = sin(x)cos(y) ⇒(∂u/∂x)=∫sin (x) cos (y) dy=sin (x) sin (y)+f(x) sin (x) sin ((π/2))+f(x)=2x ⇒f(x)=2x−sin (x) (∂u/∂x)=sin (x) [sin (y)−1]+2x ⇒u=∫{sin (x) [sin (y)−1]+2x}dx =−cos (x)[sin (y)−1]+x^2 +C −cos (π)[sin (y)−1]+π^2 +C=2 sin (y) ⇒C= sin (y)+1−π^2 ⇒u(x,y)=cos (x)+[1−cos (x)] sin (y)+x^2 +1−π^2](https://www.tinkutara.com/question/Q23446.png)
$$\:\frac{\partial^{\mathrm{2}} \mathrm{u}}{\partial\mathrm{x}\partial\mathrm{y}}\:=\:\mathrm{sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{y}\right) \\ $$$$\Rightarrow\frac{\partial\mathrm{u}}{\partial\mathrm{x}}=\int\mathrm{sin}\:\left(\mathrm{x}\right)\:\mathrm{cos}\:\left(\mathrm{y}\right)\:\mathrm{dy}=\mathrm{sin}\:\left(\mathrm{x}\right)\:\mathrm{sin}\:\left(\mathrm{y}\right)+\mathrm{f}\left(\mathrm{x}\right) \\ $$$$ \\ $$$$\mathrm{sin}\:\left(\mathrm{x}\right)\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}\right)+\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2x} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2x}−\mathrm{sin}\:\left(\mathrm{x}\right) \\ $$$$\frac{\partial\mathrm{u}}{\partial\mathrm{x}}=\mathrm{sin}\:\left(\mathrm{x}\right)\:\left[\mathrm{sin}\:\left(\mathrm{y}\right)−\mathrm{1}\right]+\mathrm{2x} \\ $$$$\Rightarrow\mathrm{u}=\int\left\{\mathrm{sin}\:\left(\mathrm{x}\right)\:\left[\mathrm{sin}\:\left(\mathrm{y}\right)−\mathrm{1}\right]+\mathrm{2x}\right\}\mathrm{dx} \\ $$$$=−\mathrm{cos}\:\left(\mathrm{x}\right)\left[\mathrm{sin}\:\left(\mathrm{y}\right)−\mathrm{1}\right]+\mathrm{x}^{\mathrm{2}} +\mathrm{C} \\ $$$$ \\ $$$$−\mathrm{cos}\:\left(\pi\right)\left[\mathrm{sin}\:\left(\mathrm{y}\right)−\mathrm{1}\right]+\pi^{\mathrm{2}} +\mathrm{C}=\mathrm{2}\:\mathrm{sin}\:\left(\mathrm{y}\right) \\ $$$$\Rightarrow\mathrm{C}=\:\mathrm{sin}\:\left(\mathrm{y}\right)+\mathrm{1}−\pi^{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow\mathrm{u}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{cos}\:\left(\mathrm{x}\right)+\left[\mathrm{1}−\mathrm{cos}\:\left(\mathrm{x}\right)\right]\:\mathrm{sin}\:\left(\mathrm{y}\right)+\mathrm{x}^{\mathrm{2}} +\mathrm{1}−\pi^{\mathrm{2}} \\ $$
Commented by tawa tawa last updated on 31/Oct/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
