Menu Close

Solve-the-equation-2-x-3-x-4-x-6-x-9-x-1-

Tinku Tara 0 Comments
Pin




Question Number 176592 by Shrinava last updated on 22/Sep/22
Solve the equation: 2^x + 3^x − 4^x + 6^x − 9^x = 1
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}: \\ $$$$\mathrm{2}^{\boldsymbol{\mathrm{x}}} \:+\:\mathrm{3}^{\boldsymbol{\mathrm{x}}} \:−\:\mathrm{4}^{\boldsymbol{\mathrm{x}}} \:+\:\mathrm{6}^{\boldsymbol{\mathrm{x}}} \:−\:\mathrm{9}^{\boldsymbol{\mathrm{x}}} \:=\:\mathrm{1} \\ $$
Answered by Frix last updated on 22/Sep/22
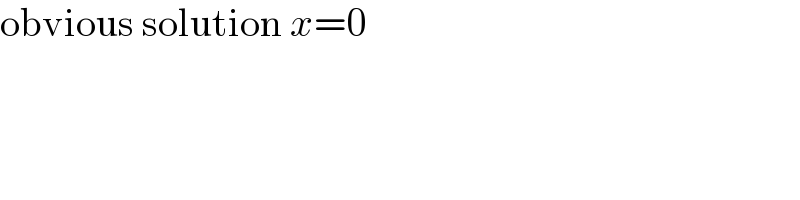
obvious solution x=0
$$\mathrm{obvious}\:\mathrm{solution}\:{x}=\mathrm{0} \\ $$
Answered by a.lgnaoui last updated on 23/Sep/22
posons a=2^x b=3^x a^2 =2^(2x) b^2 =3^(2x) ab=2^x 3^x =6^x (a+b)−(a^2 +b^2 )+ab=1 (a+b)−[(a+b)^2 −2ab]+ab=1 (a+b)−(a+b)^2 +3ab=1 (I) 2^x +3^x −(2^x +3^x )^2 =1−3×6^x (2^x +3^x )(1−2^x −3^x )=1−3×6^x (2^x +3^x )(2^(2x) +3^(2x) )=3×6^x −1 (2^x +3^x )[(2^(2x) +3^(2x) +2×6^x )−2×6^x ]=3×6^x −1 (2^x +3^x )^3 −2×6^x (2^x +3^x )=3×6^x −1 3ab=1+(a+b)^2 −(a+b) 3×6^x =1+(2^x +3^x )^2 −(2^x +3^x ) (2^x +3^x )^3 −2(2^x +3^x )((1+(2^x +3^x )^2 −(2^x +3^x ))/3)=(2^x +3^x )^2 −(2^x +3^x ) on pose (2^x +3^x =z) z^3 −(2/)(([z(1+2z^2 −z])/3)=z^2 −z z^2 −((2(1+2z^2 −z))/3)=z−1 3z^2 −4z^2 +2z−2=3z−3 z^2 +z+1=0 z=0 2^x =−3^x (−(2/3))^x =1⇒x=0 Δ=1−4=[(√3) i]^2 z1=((−1±(√3) i)/2) 2^x +3^x =(1/2)+((√3)/2)i 2(2^x +3^x )=1+(√3) i ....solutions via coshx ?
$${posons}\:\:{a}=\mathrm{2}^{{x}} \:\:{b}=\mathrm{3}^{{x}} \:\:{a}^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}{x}} \:\:{b}^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}{x}} \:\:{ab}=\mathrm{2}^{{x}} \mathrm{3}^{{x}} =\mathrm{6}^{{x}} \\ $$$$\left({a}+{b}\right)−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)+{ab}=\mathrm{1}\:\: \\ $$$$ \\ $$$$\left({a}+{b}\right)−\left[\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{2}{ab}\right]+{ab}=\mathrm{1} \\ $$$$\left({a}+{b}\right)−\left({a}+{b}\right)^{\mathrm{2}} +\mathrm{3}{ab}=\mathrm{1}\:\:\:\:\:\left(\boldsymbol{\mathrm{I}}\right) \\ $$$$\mathrm{2}^{{x}} +\mathrm{3}^{{x}} −\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)^{\mathrm{2}} =\mathrm{1}−\mathrm{3}×\mathrm{6}^{{x}} \\ $$$$\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)\left(\mathrm{1}−\mathrm{2}^{{x}} −\mathrm{3}^{{x}} \right)=\mathrm{1}−\mathrm{3}×\mathrm{6}^{{x}} \\ $$$$\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)\left(\mathrm{2}^{\mathrm{2}{x}} +\mathrm{3}^{\mathrm{2}{x}} \right)=\mathrm{3}×\mathrm{6}^{{x}} −\mathrm{1} \\ $$$$\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)\left[\left(\mathrm{2}^{\mathrm{2}{x}} +\mathrm{3}^{\mathrm{2}{x}} +\mathrm{2}×\mathrm{6}^{{x}} \right)−\mathrm{2}×\mathrm{6}^{{x}} \right]=\mathrm{3}×\mathrm{6}^{{x}} −\mathrm{1} \\ $$$$\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)^{\mathrm{3}} −\mathrm{2}×\mathrm{6}^{{x}} \left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)=\mathrm{3}×\mathrm{6}^{{x}} −\mathrm{1} \\ $$$$\mathrm{3}{ab}=\mathrm{1}+\left({a}+{b}\right)^{\mathrm{2}} −\left({a}+{b}\right) \\ $$$$\mathrm{3}×\mathrm{6}^{{x}} =\mathrm{1}+\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)^{\mathrm{2}} −\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right) \\ $$$$\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)^{\mathrm{3}} −\mathrm{2}\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)\frac{\mathrm{1}+\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)^{\mathrm{2}} −\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)}{\mathrm{3}}=\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)^{\mathrm{2}} −\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right) \\ $$$${on}\:{pose}\:\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} ={z}\right) \\ $$$${z}^{\mathrm{3}} −\frac{\mathrm{2}}{}\frac{\left[{z}\left(\mathrm{1}+\mathrm{2}{z}^{\mathrm{2}} −{z}\right]\right.}{\mathrm{3}}={z}^{\mathrm{2}} −{z} \\ $$$${z}^{\mathrm{2}} −\frac{\mathrm{2}\left(\mathrm{1}+\mathrm{2}{z}^{\mathrm{2}} −{z}\right)}{\mathrm{3}}={z}−\mathrm{1} \\ $$$$\mathrm{3}{z}^{\mathrm{2}} −\mathrm{4}{z}^{\mathrm{2}} +\mathrm{2}{z}−\mathrm{2}=\mathrm{3}{z}−\mathrm{3} \\ $$$${z}^{\mathrm{2}} +{z}+\mathrm{1}=\mathrm{0}\:\:\:\:\:\:{z}=\mathrm{0} \\ $$$$\mathrm{2}^{{x}} =−\mathrm{3}^{{x}} \:\:\:\:\left(−\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} =\mathrm{1}\Rightarrow{x}=\mathrm{0} \\ $$$$\Delta=\mathrm{1}−\mathrm{4}=\left[\sqrt{\mathrm{3}}\:{i}\right]^{\mathrm{2}} \\ $$$${z}\mathrm{1}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{3}}\:{i}}{\mathrm{2}} \\ $$$$\mathrm{2}^{{x}} +\mathrm{3}^{{x}} =\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i} \\ $$$$\mathrm{2}\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)=\mathrm{1}+\sqrt{\mathrm{3}}\:{i} \\ $$$$….{solutions}\:\:{via}\:\:\:\:{coshx}\:? \\ $$
Commented by Shrinava last updated on 23/Sep/22
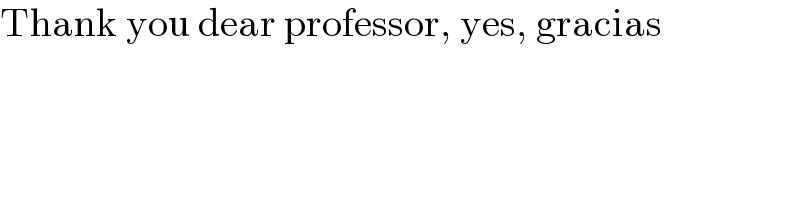
Thank you dear professor, yes, gracias
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor},\:\mathrm{yes},\:\mathrm{gracias} \\ $$
Commented by Frix last updated on 23/Sep/22
(a+b)−(a^2 +b^2 )+ab=1 a=u−v∧b=u+v 2u−(2u^2 +2v^2 )+u^2 −v^2 =1 2u−u^2 −3v^2 =1 v^2 =−(((u−1)^2 )/3) v=±((u−1)/( (√3)))i a=u±(((√3)(u−1))/3)i∧b=u∓(((√3)(u−1))/3)i 2^x =u±(((√3)(u−1))/3)i∧3^x =u∓(((√3)(u−1))/3)i again obviously x=0∧u=1 x=((ln (u±(((√3)(u−1))/3)i) +2n_1 πi)/(ln 2))∧x=((ln (u∓(((√3)(u−1))/3)i) +2n_2 πi)/(ln 3)) I don′t think we can find n_1 , n_2 ∈Z for u≠1 p±qi=(√(p^2 +q^2 ))e^(±i tan^(−1) (q/p)) ln (p±qi) =((ln (p^2 +q^2 ))/2)+(2nπ±tan^(−1) (q/p))i we have ((ln (p−qi))/(ln 2))=((ln (p+qi))/(ln 3)) we need ((2n_1 π−tan^(−1) t)/(ln 2))=((2n_2 π+tan^(−1) t)/(ln 3)) ⇔ n_2 =((1−((ln 3)/(ln 2)))/(2π))tan^(−1) t +((ln 3)/(ln 2))n_1 with n_1 , n_2 ∈Z
$$\left({a}+{b}\right)−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)+{ab}=\mathrm{1} \\ $$$${a}={u}−{v}\wedge{b}={u}+{v} \\ $$$$\mathrm{2}{u}−\left(\mathrm{2}{u}^{\mathrm{2}} +\mathrm{2}{v}^{\mathrm{2}} \right)+{u}^{\mathrm{2}} −{v}^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{2}{u}−{u}^{\mathrm{2}} −\mathrm{3}{v}^{\mathrm{2}} =\mathrm{1} \\ $$$${v}^{\mathrm{2}} =−\frac{\left({u}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}} \\ $$$${v}=\pm\frac{{u}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{i} \\ $$$${a}={u}\pm\frac{\sqrt{\mathrm{3}}\left({u}−\mathrm{1}\right)}{\mathrm{3}}\mathrm{i}\wedge{b}={u}\mp\frac{\sqrt{\mathrm{3}}\left({u}−\mathrm{1}\right)}{\mathrm{3}}\mathrm{i} \\ $$$$\mathrm{2}^{{x}} ={u}\pm\frac{\sqrt{\mathrm{3}}\left({u}−\mathrm{1}\right)}{\mathrm{3}}\mathrm{i}\wedge\mathrm{3}^{{x}} ={u}\mp\frac{\sqrt{\mathrm{3}}\left({u}−\mathrm{1}\right)}{\mathrm{3}}\mathrm{i} \\ $$$$\mathrm{again}\:\mathrm{obviously}\:{x}=\mathrm{0}\wedge{u}=\mathrm{1} \\ $$$${x}=\frac{\mathrm{ln}\:\left({u}\pm\frac{\sqrt{\mathrm{3}}\left({u}−\mathrm{1}\right)}{\mathrm{3}}\mathrm{i}\right)\:+\mathrm{2}{n}_{\mathrm{1}} \pi\mathrm{i}}{\mathrm{ln}\:\mathrm{2}}\wedge{x}=\frac{\mathrm{ln}\:\left({u}\mp\frac{\sqrt{\mathrm{3}}\left({u}−\mathrm{1}\right)}{\mathrm{3}}\mathrm{i}\right)\:+\mathrm{2}{n}_{\mathrm{2}} \pi\mathrm{i}}{\mathrm{ln}\:\mathrm{3}} \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:{n}_{\mathrm{1}} ,\:{n}_{\mathrm{2}} \in\mathbb{Z}\:\mathrm{for}\:{u}\neq\mathrm{1} \\ $$$${p}\pm{q}\mathrm{i}=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }\mathrm{e}^{\pm\mathrm{i}\:\mathrm{tan}^{−\mathrm{1}} \:\frac{{q}}{{p}}} \\ $$$$\mathrm{ln}\:\left({p}\pm{q}\mathrm{i}\right)\:=\frac{\mathrm{ln}\:\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)}{\mathrm{2}}+\left(\mathrm{2}{n}\pi\pm\mathrm{tan}^{−\mathrm{1}} \:\frac{{q}}{{p}}\right)\mathrm{i} \\ $$$$\mathrm{we}\:\mathrm{have} \\ $$$$\frac{\mathrm{ln}\:\left({p}−{q}\mathrm{i}\right)}{\mathrm{ln}\:\mathrm{2}}=\frac{\mathrm{ln}\:\left({p}+{q}\mathrm{i}\right)}{\mathrm{ln}\:\mathrm{3}} \\ $$$$\mathrm{we}\:\mathrm{need} \\ $$$$\frac{\mathrm{2}{n}_{\mathrm{1}} \pi−\mathrm{tan}^{−\mathrm{1}} \:{t}}{\mathrm{ln}\:\mathrm{2}}=\frac{\mathrm{2}{n}_{\mathrm{2}} \pi+\mathrm{tan}^{−\mathrm{1}} \:{t}}{\mathrm{ln}\:\mathrm{3}} \\ $$$$\Leftrightarrow \\ $$$${n}_{\mathrm{2}} =\frac{\mathrm{1}−\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{2}}}{\mathrm{2}\pi}\mathrm{tan}^{−\mathrm{1}} \:{t}\:+\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{2}}{n}_{\mathrm{1}} \:\mathrm{with}\:{n}_{\mathrm{1}} ,\:{n}_{\mathrm{2}} \in\mathbb{Z} \\ $$
Commented by a.lgnaoui last updated on 23/Sep/22
thank you
$${thank}\:{you} \\ $$
Commented by Tawa11 last updated on 23/Sep/22
Great sirs
$$\mathrm{Great}\:\mathrm{sirs} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *