Question Number 100879 by Tony6400 last updated on 29/Jun/20
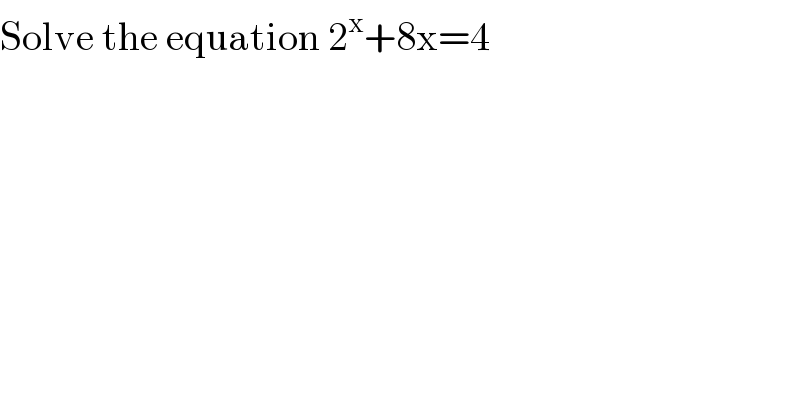
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{2}^{\mathrm{x}} +\mathrm{8x}=\mathrm{4} \\ $$
Commented by bemath last updated on 29/Jun/20
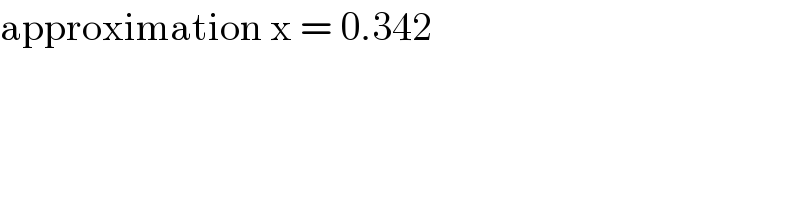
$$\mathrm{approximation}\:\mathrm{x}\:=\:\mathrm{0}.\mathrm{342} \\ $$
Answered by 1549442205 last updated on 07/Jul/20

$$\Leftrightarrow\mathrm{2}^{\mathrm{x}−\mathrm{2}} +\mathrm{2x}−\mathrm{1}=\mathrm{0}.\mathrm{Putting}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2}^{\mathrm{x}−\mathrm{2}} +\mathrm{2x}−\mathrm{1} \\ $$$$\mathrm{f}\:'\left(\mathrm{x}\right)=\mathrm{2}^{\mathrm{x}−\mathrm{2}} \mathrm{ln2}+\mathrm{2}>\mathrm{0}\forall\mathrm{x}\in\left(−\infty;+\infty\right) \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{0}\Leftrightarrow\mathrm{x}=\mathrm{0}.\mathrm{3416043768} \\ $$$$\mathrm{Since}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{increasing}\:,\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{has} \\ $$$$\boldsymbol{\mathrm{only}}\:\boldsymbol{\mathrm{root}}\:\boldsymbol{\mathrm{x}}=\mathrm{0}.\mathrm{3416043768} \\ $$
Answered by mr W last updated on 29/Jun/20
![2^x =8((1/2)−x) e^(xln 2) =8((1/2)−x) (((√2) ln 2)/8) =[((1/2)−x)ln 2]e^(((1/2)−x)ln 2) ((1/2)−x)ln 2=W((((√2) ln 2)/8)) ⇒x=(1/2)−(1/(ln 2))W((((√2) ln 2)/8)) ≈(1/2)−((0.109791)/(ln 2))=0.341605](https://www.tinkutara.com/question/Q100898.png)
$$\mathrm{2}^{{x}} =\mathrm{8}\left(\frac{\mathrm{1}}{\mathrm{2}}−{x}\right) \\ $$$${e}^{{x}\mathrm{ln}\:\mathrm{2}} =\mathrm{8}\left(\frac{\mathrm{1}}{\mathrm{2}}−{x}\right) \\ $$$$\frac{\sqrt{\mathrm{2}}\:\mathrm{ln}\:\mathrm{2}}{\mathrm{8}}\:=\left[\left(\frac{\mathrm{1}}{\mathrm{2}}−{x}\right)\mathrm{ln}\:\mathrm{2}\right]{e}^{\left(\frac{\mathrm{1}}{\mathrm{2}}−{x}\right)\mathrm{ln}\:\mathrm{2}} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}−{x}\right)\mathrm{ln}\:\mathrm{2}={W}\left(\frac{\sqrt{\mathrm{2}}\:\mathrm{ln}\:\mathrm{2}}{\mathrm{8}}\right) \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{ln}\:\mathrm{2}}{W}\left(\frac{\sqrt{\mathrm{2}}\:\mathrm{ln}\:\mathrm{2}}{\mathrm{8}}\right) \\ $$$$\approx\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{0}.\mathrm{109791}}{\mathrm{ln}\:\mathrm{2}}=\mathrm{0}.\mathrm{341605} \\ $$
