Question Number 168043 by Sigunur last updated on 01/Apr/22

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}: \\ $$$$\frac{\mathrm{7x}^{\mathrm{2}} \:+\:\mathrm{7}}{\:\sqrt{\mathrm{7x}^{\mathrm{2}} \:+\:\mathrm{3}}}\:+\:\frac{\mathrm{y}^{\mathrm{2}} \:+\:\mathrm{18}}{\:\sqrt{\mathrm{y}^{\mathrm{2}} \:+\:\mathrm{17}}}\:+\:\frac{\mathrm{3z}^{\mathrm{2}} \:+\:\mathrm{26}}{\:\sqrt{\mathrm{3z}^{\mathrm{2}} \:+\:\mathrm{1}}}\:=\:\mathrm{16} \\ $$
Commented by MJS_new last updated on 01/Apr/22

$$\mathrm{the}\:\mathrm{minimum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{lhs}\:\mathrm{for}\:{x},\:{y},\:{z}\:\in\mathbb{R}\:\mathrm{is} \\ $$$$\mathrm{4}+\frac{\mathrm{18}}{\:\sqrt{\mathrm{17}}}+\mathrm{10}\approx\mathrm{18}.\mathrm{37}>\mathrm{16}\:\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$$\mathrm{for}\:{x},\:{y},\:{z}\:\in\mathbb{C}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{not}\:\mathrm{unique} \\ $$
Answered by yogamulyadi last updated on 01/Apr/22

$$\frac{\mathrm{7}{x}^{\mathrm{2}} +\mathrm{3}+\mathrm{4}}{\:\sqrt{\mathrm{7}{x}^{\mathrm{2}} +\mathrm{3}}}+\frac{{y}^{\mathrm{2}} +\mathrm{17}+\mathrm{1}}{\:\sqrt{{y}^{\mathrm{2}} +\mathrm{17}}}+\frac{\mathrm{3}{z}^{\mathrm{2}} +\mathrm{1}+\mathrm{25}}{\:\sqrt{\mathrm{3}{z}^{\mathrm{2}} +\mathrm{1}}}=\mathrm{16} \\ $$$$\mathrm{2}+\mathrm{2}+\mathrm{1}+\mathrm{1}+\mathrm{5}+\mathrm{5}=\mathrm{16} \\ $$$$\mathrm{7}{x}^{\mathrm{2}} +\mathrm{3}=\mathrm{2}^{\mathrm{2}} ,\:{y}^{\mathrm{2}} +\mathrm{17}=\mathrm{1}^{\mathrm{2}} ,\:\mathrm{3}{z}^{\mathrm{2}} +\mathrm{1}=\mathrm{5}^{\mathrm{2}} \\ $$$${x}=\pm\frac{\mathrm{1}}{\mathrm{7}}\:,\:{y}=\pm\mathrm{4}{i}\:,\:{z}=\pm\mathrm{2}\sqrt{\mathrm{2}} \\ $$
Commented by Sigunur last updated on 01/Apr/22
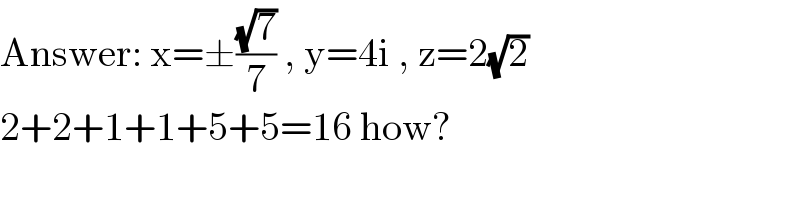
$$\mathrm{Answer}:\:\mathrm{x}=\pm\frac{\sqrt{\mathrm{7}}}{\mathrm{7}}\:,\:\mathrm{y}=\mathrm{4i}\:,\:\mathrm{z}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\mathrm{2}+\mathrm{2}+\mathrm{1}+\mathrm{1}+\mathrm{5}+\mathrm{5}=\mathrm{16}\:\mathrm{how}? \\ $$
