Menu Close

Solve-the-equation-cos-4-x-i-sin-4-x-4e-4ix-

Tinku Tara 0 Comments
Pin




Question Number 150058 by mathdanisur last updated on 09/Aug/21
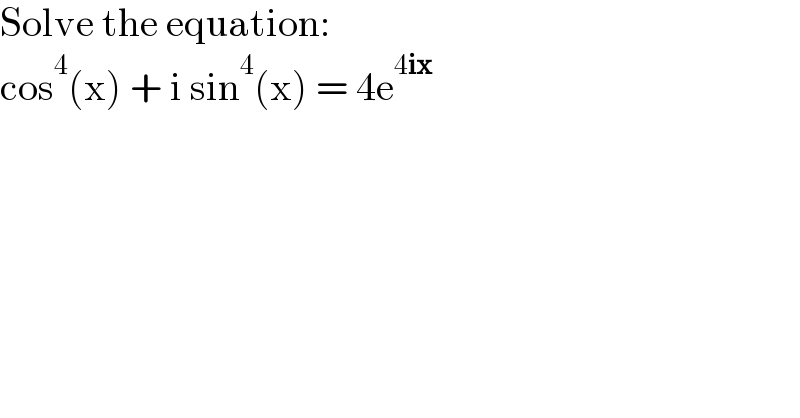
Solve the equation: cos^4 (x) + i sin^4 (x) = 4e^(4ix)
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}: \\ $$$$\mathrm{cos}^{\mathrm{4}} \left(\mathrm{x}\right)\:+\:\mathrm{i}\:\mathrm{sin}^{\mathrm{4}} \left(\mathrm{x}\right)\:=\:\mathrm{4e}^{\mathrm{4}\boldsymbol{\mathrm{ix}}} \\ $$
Commented by MJS_new last updated on 10/Aug/21
I found these (n∈Z): x≈nπ+.866946376+.432060893i x≈nπ+.00142216354+.301698277i x≈nπ−.768959527+.828028492i x≈nπ−1.26957042+.336555887i
$$\mathrm{I}\:\mathrm{found}\:\mathrm{these}\:\left({n}\in\mathbb{Z}\right): \\ $$$${x}\approx{n}\pi+.\mathrm{866946376}+.\mathrm{432060893i} \\ $$$${x}\approx{n}\pi+.\mathrm{00142216354}+.\mathrm{301698277i} \\ $$$${x}\approx{n}\pi−.\mathrm{768959527}+.\mathrm{828028492i} \\ $$$${x}\approx{n}\pi−\mathrm{1}.\mathrm{26957042}+.\mathrm{336555887i} \\ $$
Commented by mathdanisur last updated on 10/Aug/21
Thank you Ser
$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
Answered by MJS_new last updated on 10/Aug/21
((√2)/4)≤∣cos^4 x +i sin^4 x∣≤1 ∣4e^(4ix) ∣=4 ⇒ no solution ∈R
$$\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\leqslant\mid\mathrm{cos}^{\mathrm{4}} \:{x}\:+\mathrm{i}\:\mathrm{sin}^{\mathrm{4}} \:{x}\mid\leqslant\mathrm{1} \\ $$$$\mid\mathrm{4e}^{\mathrm{4i}{x}} \mid=\mathrm{4} \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{solution}\:\in\mathbb{R} \\ $$
Commented by mathdanisur last updated on 09/Aug/21
Thankyou Ser Dear Ser, no solution in real numbers, but it has a complex number solution
$$\mathrm{Thankyou}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$$$\mathrm{Dear}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{no}\:\mathrm{solution}\:\mathrm{in}\:\mathrm{real}\:\mathrm{numbers},\:\mathrm{but}\:\mathrm{it} \\ $$$$\mathrm{has}\:\mathrm{a}\:\mathrm{complex}\:\mathrm{number}\:\mathrm{solution} \\ $$
Answered by MJS_new last updated on 10/Aug/21
cos^4 x +i sin^4 x =4e^(4ix) cos^4 x +i sin^4 x =4cos 4x +4i sin 4x let t=tan x (1/((t^2 +1)^2 ))+(t^4 /((t^2 +1)^2 ))i=((4(t^2 −2t−1)(t^2 +2t−1))/((t^2 +1)^2 ))−((16t(t−1)(t+1))/((t^2 +1)^2 ))i this leads to t^4 +((16(1−4i))/(17))t^3 −((24(4+i))/(17))t^2 −((16(1−4i))/(17))t+((3(4+i))/(17))=0 I found no useful exact solution t_1 ≈.799102359+.790210727i t_2 ≈.00130018452+.292866540i t_3 ≈−.363754201+.918561793i t_4 ≈−1.37782481+1.76306682i t=tan x ⇔ x=nπ+arctan t ⇒ the solutions I posted above
$$\mathrm{cos}^{\mathrm{4}} \:{x}\:+\mathrm{i}\:\mathrm{sin}^{\mathrm{4}} \:{x}\:=\mathrm{4e}^{\mathrm{4i}{x}} \\ $$$$\mathrm{cos}^{\mathrm{4}} \:{x}\:+\mathrm{i}\:\mathrm{sin}^{\mathrm{4}} \:{x}\:=\mathrm{4cos}\:\mathrm{4}{x}\:+\mathrm{4i}\:\mathrm{sin}\:\mathrm{4}{x} \\ $$$$\mathrm{let}\:{t}=\mathrm{tan}\:{x} \\ $$$$\frac{\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{{t}^{\mathrm{4}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{i}=\frac{\mathrm{4}\left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{16}{t}\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{i} \\ $$$$\mathrm{this}\:\mathrm{leads}\:\mathrm{to} \\ $$$${t}^{\mathrm{4}} +\frac{\mathrm{16}\left(\mathrm{1}−\mathrm{4i}\right)}{\mathrm{17}}{t}^{\mathrm{3}} −\frac{\mathrm{24}\left(\mathrm{4}+\mathrm{i}\right)}{\mathrm{17}}{t}^{\mathrm{2}} −\frac{\mathrm{16}\left(\mathrm{1}−\mathrm{4i}\right)}{\mathrm{17}}{t}+\frac{\mathrm{3}\left(\mathrm{4}+\mathrm{i}\right)}{\mathrm{17}}=\mathrm{0} \\ $$$$\mathrm{I}\:\mathrm{found}\:\mathrm{no}\:\mathrm{useful}\:\mathrm{exact}\:\mathrm{solution} \\ $$$${t}_{\mathrm{1}} \approx.\mathrm{799102359}+.\mathrm{790210727i} \\ $$$${t}_{\mathrm{2}} \approx.\mathrm{00130018452}+.\mathrm{292866540i} \\ $$$${t}_{\mathrm{3}} \approx−.\mathrm{363754201}+.\mathrm{918561793i} \\ $$$${t}_{\mathrm{4}} \approx−\mathrm{1}.\mathrm{37782481}+\mathrm{1}.\mathrm{76306682i} \\ $$$${t}=\mathrm{tan}\:{x}\:\Leftrightarrow\:{x}={n}\pi+\mathrm{arctan}\:{t} \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{solutions}\:\mathrm{I}\:\mathrm{posted}\:\mathrm{above} \\ $$
Commented by mathdanisur last updated on 10/Aug/21
Thank You Ser
$$\mathrm{Thank}\:\mathrm{You}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *