Question Number 87724 by mr W last updated on 05/Apr/20
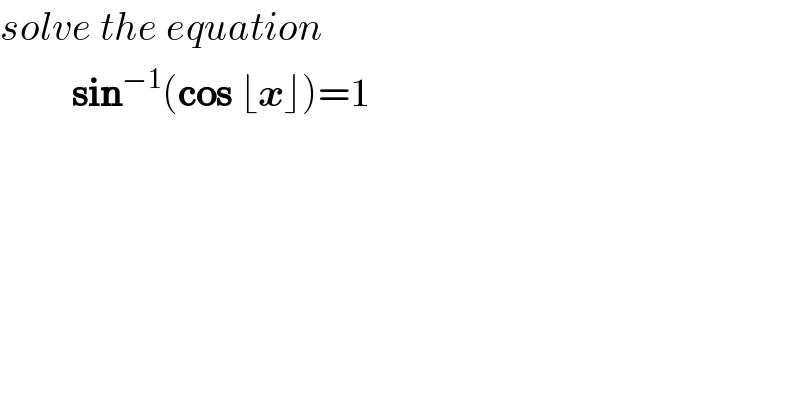
$${solve}\:{the}\:{equation} \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{sin}}^{−\mathrm{1}} \left(\boldsymbol{\mathrm{cos}}\:\lfloor\boldsymbol{{x}}\rfloor\right)=\mathrm{1} \\ $$
Answered by mahdi last updated on 05/Apr/20
![sin^(−1) (cos[x])=1⇒cos[x]=sin(1+2kπ) cos[x]=cos((π/2)−(1+2kπ))= cos(−(1+((4k−1)/2)π))=cos(1+((4k−1)/2)π) ⇒[x]=1+((4k−1)/2)π ⇒^([x]∈Z) 1+((4k−1)/2)π∈Z (but:1+((4k−1)/2)π∉Z for:k∈Z)⇒without ans](https://www.tinkutara.com/question/Q87736.png)
$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{cos}\left[\mathrm{x}\right]\right)=\mathrm{1}\Rightarrow\mathrm{cos}\left[\mathrm{x}\right]=\mathrm{sin}\left(\mathrm{1}+\mathrm{2k}\pi\right) \\ $$$$\mathrm{cos}\left[\mathrm{x}\right]=\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\left(\mathrm{1}+\mathrm{2k}\pi\right)\right)= \\ $$$$\mathrm{cos}\left(−\left(\mathrm{1}+\frac{\mathrm{4k}−\mathrm{1}}{\mathrm{2}}\pi\right)\right)=\mathrm{cos}\left(\mathrm{1}+\frac{\mathrm{4k}−\mathrm{1}}{\mathrm{2}}\pi\right) \\ $$$$\Rightarrow\left[\mathrm{x}\right]=\mathrm{1}+\frac{\mathrm{4k}−\mathrm{1}}{\mathrm{2}}\pi\:\:\overset{\left[\mathrm{x}\right]\in\mathrm{Z}} {\Rightarrow}\:\mathrm{1}+\frac{\mathrm{4k}−\mathrm{1}}{\mathrm{2}}\pi\in\mathrm{Z} \\ $$$$\left(\mathrm{but}:\mathrm{1}+\frac{\mathrm{4k}−\mathrm{1}}{\mathrm{2}}\pi\notin\mathrm{Z}\:\:\mathrm{for}:\mathrm{k}\in\mathrm{Z}\right)\Rightarrow\mathrm{without}\:\mathrm{ans} \\ $$
Commented by mr W last updated on 05/Apr/20

$${thank}\:{you}\:{sir}!\:{i}\:{have}\:{expected}\:{this} \\ $$$${comfirmation},\:{see}\:{Q}\mathrm{87625}. \\ $$
Commented by mahdi last updated on 06/Apr/20

$$\mathrm{Mr}.\mathrm{w},\:\:\mathrm{1rad}\:\:\mathrm{or}\:\:\mathrm{1deg}?\mathrm{if}\:\mathrm{1rad}\:\mathrm{my} \\ $$$$\mathrm{ans}\:\mathrm{correct}.\mathrm{but}\:\mathrm{if}\:\mathrm{1deg}\:\mathrm{not}\:\mathrm{correct}. \\ $$
Commented by mr W last updated on 06/Apr/20

$$\mathrm{1}\:{rad} \\ $$
