Question Number 150670 by EDWIN88 last updated on 14/Aug/21
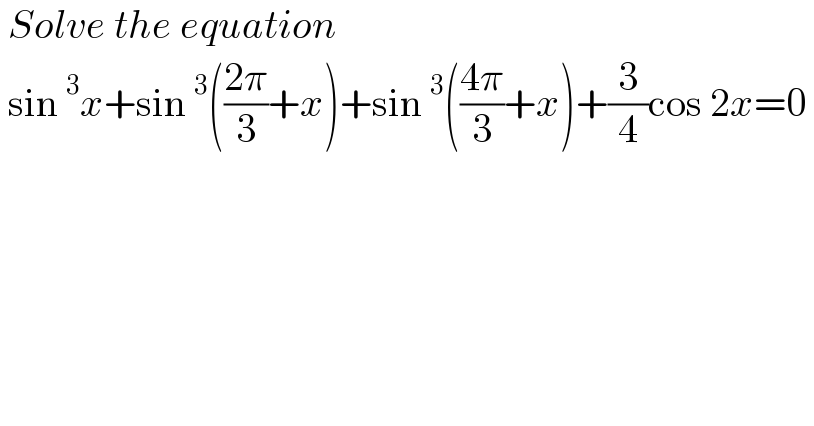
$$\:{Solve}\:{the}\:{equation}\: \\ $$$$\:\mathrm{sin}\:^{\mathrm{3}} {x}+\mathrm{sin}\:^{\mathrm{3}} \left(\frac{\mathrm{2}\pi}{\mathrm{3}}+{x}\right)+\mathrm{sin}\:^{\mathrm{3}} \left(\frac{\mathrm{4}\pi}{\mathrm{3}}+{x}\right)+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{cos}\:\mathrm{2}{x}=\mathrm{0}\: \\ $$
Answered by EDWIN88 last updated on 14/Aug/21

Answered by ajfour last updated on 14/Aug/21
![sin 3x=3sin x−4sin^3 x ⇒ (3sin x−sin 3x) −[3sin (x−(π/3))−sin 3x] −[3sin (x+(π/3))−sin 3x] +3cos 2x=0 ⇒ 3sin x+3cos 2x+3sin 3x −3sin x=0 ⇒ cos 2x+sin 3x=0 ⇒ 1+2s^2 +3s−4s^3 =0 ∀ s=sin x x_i = nπ+(−1)^n sin^(−1) s_i](https://www.tinkutara.com/question/Q150675.png)
$$\mathrm{sin}\:\mathrm{3}{x}=\mathrm{3sin}\:{x}−\mathrm{4sin}\:^{\mathrm{3}} {x} \\ $$$$\Rightarrow\:\left(\mathrm{3sin}\:{x}−\mathrm{sin}\:\mathrm{3}{x}\right) \\ $$$$\:\:\:\:\:−\left[\mathrm{3sin}\:\left({x}−\frac{\pi}{\mathrm{3}}\right)−\mathrm{sin}\:\mathrm{3}{x}\right] \\ $$$$\:\:\:\:\:−\left[\mathrm{3sin}\:\left({x}+\frac{\pi}{\mathrm{3}}\right)−\mathrm{sin}\:\mathrm{3}{x}\right] \\ $$$$\:\:\:\:+\mathrm{3cos}\:\mathrm{2}{x}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{3sin}\:{x}+\mathrm{3cos}\:\mathrm{2}{x}+\mathrm{3sin}\:\mathrm{3}{x} \\ $$$$\:\:\:\:−\mathrm{3sin}\:{x}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{cos}\:\mathrm{2}{x}+\mathrm{sin}\:\mathrm{3}{x}=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{1}+\mathrm{2}{s}^{\mathrm{2}} +\mathrm{3}{s}−\mathrm{4}{s}^{\mathrm{3}} =\mathrm{0} \\ $$$$\forall\:\:\:\:{s}=\mathrm{sin}\:{x} \\ $$$${x}_{{i}} =\:{n}\pi+\left(−\mathrm{1}\right)^{{n}} \mathrm{sin}^{−\mathrm{1}} {s}_{{i}} \\ $$
Answered by MJS_new last updated on 14/Aug/21
![sin ((2π+3x)/3) =(((√3)cos x −sin x)/2) sin ((4π+3x)/3) =−(((√3)cos x +sin x)/2) cos 2x =2cos^2 x −1 s^3 +(1/8)((√3)c−s)^3 −(1/8)((√3)c+s)^3 +(3/2)c^2 −(3/4)=0 s^3 −3c^2 s+2c^2 −1=0 [c^2 =1−s^2 ] s^3 −(1/2)s^2 −(3/4)s+(1/4)=0 (s−1)(s^2 +(s/2)−(1/4))=0 ... ⇒ for 0≤x<2π: x∈{(π/(10)), ((5π)/(10)), ((9π)/(10)), ((13π)/(10)), ((17π)/(10))} generally x=((4k+1)/(10))π+2nπ with n∈Z∧k=0, 1, 2, 3, 4](https://www.tinkutara.com/question/Q150679.png)
$$\mathrm{sin}\:\frac{\mathrm{2}\pi+\mathrm{3}{x}}{\mathrm{3}}\:=\frac{\sqrt{\mathrm{3}}\mathrm{cos}\:{x}\:−\mathrm{sin}\:{x}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\frac{\mathrm{4}\pi+\mathrm{3}{x}}{\mathrm{3}}\:=−\frac{\sqrt{\mathrm{3}}\mathrm{cos}\:{x}\:+\mathrm{sin}\:{x}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\mathrm{2}{x}\:=\mathrm{2cos}^{\mathrm{2}} \:{x}\:−\mathrm{1} \\ $$$${s}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{8}}\left(\sqrt{\mathrm{3}}{c}−{s}\right)^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{8}}\left(\sqrt{\mathrm{3}}{c}+{s}\right)^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{2}}{c}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}=\mathrm{0} \\ $$$${s}^{\mathrm{3}} −\mathrm{3}{c}^{\mathrm{2}} {s}+\mathrm{2}{c}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\left[{c}^{\mathrm{2}} =\mathrm{1}−{s}^{\mathrm{2}} \right] \\ $$$${s}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}{s}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}{s}+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\left({s}−\mathrm{1}\right)\left({s}^{\mathrm{2}} +\frac{{s}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\right)=\mathrm{0} \\ $$$$… \\ $$$$\Rightarrow \\ $$$$\mathrm{for}\:\mathrm{0}\leqslant{x}<\mathrm{2}\pi: \\ $$$${x}\in\left\{\frac{\pi}{\mathrm{10}},\:\frac{\mathrm{5}\pi}{\mathrm{10}},\:\frac{\mathrm{9}\pi}{\mathrm{10}},\:\frac{\mathrm{13}\pi}{\mathrm{10}},\:\frac{\mathrm{17}\pi}{\mathrm{10}}\right\} \\ $$$$\mathrm{generally}\:{x}=\frac{\mathrm{4}{k}+\mathrm{1}}{\mathrm{10}}\pi+\mathrm{2}{n}\pi\:\mathrm{with}\:{n}\in\mathbb{Z}\wedge{k}=\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4} \\ $$
