Menu Close

solve-the-equation-sin-x-sin-2x-sin-3x-cos-x-cos-2x-cos-3x-

Tinku Tara 0 Comments
Pin




Question Number 64475 by aliesam last updated on 18/Jul/19
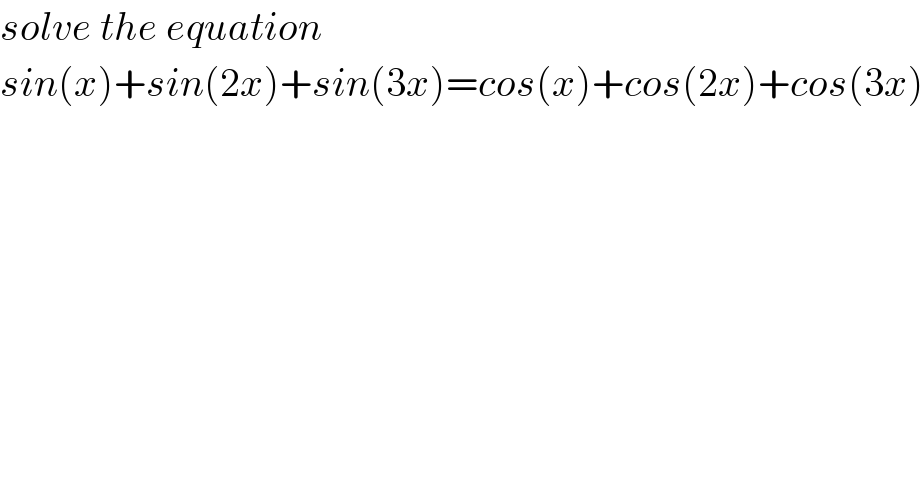
solve the equation sin(x)+sin(2x)+sin(3x)=cos(x)+cos(2x)+cos(3x)
$${solve}\:{the}\:{equation} \\ $$$${sin}\left({x}\right)+{sin}\left(\mathrm{2}{x}\right)+{sin}\left(\mathrm{3}{x}\right)={cos}\left({x}\right)+{cos}\left(\mathrm{2}{x}\right)+{cos}\left(\mathrm{3}{x}\right) \\ $$
Commented by mathmax by abdo last updated on 18/Jul/19
let u_n =Σ_(k=0) ^n sin(kx) and v_n =Σ_(k=0) ^n cos(kx) ⇒ u_n =Im(Σ_(k=0) ^n e^(ikx) ) and Σ_(k=0) ^n e^(ikx) =Σ_(k=0) ^n (e^(ix) )^k =((1−e^((n+1)ix) )/(1−e^(ix) )) if e^(ix) ≠1 )=((1−cos(n+1)x−isin(n+1)x)/(1−cosx−isinx)) =((2sin^2 (((n+1)x)/2)−2isin((((n+1)x)/2))cos((((n+1)x)/2)))/(2sin^2 ((x/2))−2isin((x/2))cos((x/2)))) =((−isin((((n+1)x)/2)){cos((((n+1)x)/2))+isin((((n+1)x)/2)))/(−isin((x/2))(cos((x/2))+isin((x/2)))) =((sin((((n+1)x)/2)))/(sin((x/2)))) e^((inx)/2) ⇒u_n =((sin((((n+1)x)/2)))/(sin((x/2)))) sin(((nx)/2)) v_n =Σ_(k=0) ^n cos(kx) =Re(Σ_(k=0) ^n e^(ikx) ) =((sin((((n+1)x)/2))cos(((nx)/2)))/(sin((x/2)))) ⇒u_3 =((sin(2x))/(sin((x/2)))) ×sin(((3x)/2)) =sinx +sin(2x)+sin(3x) v_3 =((sin(2x))/(sin((x/2))))cos(((3x)/2)) =1+cosx +cos(2x)+cos(3x) if we consider the equation sinx +sin(2x)+sin(3x) =1+cosx +cos(2x)+cos(3x) we get (e) ⇔u_3 =v_3 ⇒sin(((3x)/2))=cos(((3x)/2)) ⇒cos((π/2)−((3x)/2))=cos(((3x)/2)) ⇒ ((3x)/2) =(π/2)−((3x)/2) +2kπ or ((3x)/2) =−(π/2) +((3x)/2) +2kπ ⇒ 3x =(π/2) +2kπ or 2kπ=(π/2)(→impossible) ⇒x=(π/6) +((2kπ)/3) k ∈Z if we consider sinx +sin(2x)+sin(3x)=cosx +cos(2x) +cos(3x) we solve u_3 =v_3 −1 but you find a lots of calculus...
$${let}\:{u}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} {sin}\left({kx}\right)\:{and}\:{v}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{cos}\left({kx}\right)\:\Rightarrow \\ $$$${u}_{{n}} ={Im}\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{e}^{{ikx}} \right)\:\:{and}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{e}^{{ikx}} \:=\sum_{{k}=\mathrm{0}} ^{{n}} \:\left({e}^{{ix}} \right)^{{k}} \:=\frac{\mathrm{1}−{e}^{\left({n}+\mathrm{1}\right){ix}} }{\mathrm{1}−{e}^{{ix}} } \\ $$$$\left.{if}\:{e}^{{ix}} \neq\mathrm{1}\:\right)=\frac{\mathrm{1}−{cos}\left({n}+\mathrm{1}\right){x}−{isin}\left({n}+\mathrm{1}\right){x}}{\mathrm{1}−{cosx}−{isinx}} \\ $$$$=\frac{\mathrm{2}{sin}^{\mathrm{2}} \frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}−\mathrm{2}{isin}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right){cos}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)}{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{2}{isin}\left(\frac{{x}}{\mathrm{2}}\right){cos}\left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$$=\frac{−{isin}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)\left\{{cos}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)+{isin}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)\right.}{−{isin}\left(\frac{{x}}{\mathrm{2}}\right)\left({cos}\left(\frac{{x}}{\mathrm{2}}\right)+{isin}\left(\frac{{x}}{\mathrm{2}}\right)\right.} \\ $$$$=\frac{{sin}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)}\:{e}^{\frac{{inx}}{\mathrm{2}}} \:\Rightarrow{u}_{{n}} =\frac{{sin}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)}\:{sin}\left(\frac{{nx}}{\mathrm{2}}\right) \\ $$$${v}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{cos}\left({kx}\right)\:={Re}\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{e}^{{ikx}} \right)\:=\frac{{sin}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right){cos}\left(\frac{{nx}}{\mathrm{2}}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$$\Rightarrow{u}_{\mathrm{3}} =\frac{{sin}\left(\mathrm{2}{x}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)}\:\:×{sin}\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\:={sinx}\:+{sin}\left(\mathrm{2}{x}\right)+{sin}\left(\mathrm{3}{x}\right) \\ $$$${v}_{\mathrm{3}} =\frac{{sin}\left(\mathrm{2}{x}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)}{cos}\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\:=\mathrm{1}+{cosx}\:+{cos}\left(\mathrm{2}{x}\right)+{cos}\left(\mathrm{3}{x}\right) \\ $$$${if}\:{we}\:{consider}\:{the}\:{equation}\:{sinx}\:+{sin}\left(\mathrm{2}{x}\right)+{sin}\left(\mathrm{3}{x}\right) \\ $$$$=\mathrm{1}+{cosx}\:+{cos}\left(\mathrm{2}{x}\right)+{cos}\left(\mathrm{3}{x}\right)\:{we}\:{get} \\ $$$$\left({e}\right)\:\Leftrightarrow{u}_{\mathrm{3}} ={v}_{\mathrm{3}} \:\Rightarrow{sin}\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)={cos}\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\:\Rightarrow{cos}\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{3}{x}}{\mathrm{2}}\right)={cos}\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{3}{x}}{\mathrm{2}}\:=\frac{\pi}{\mathrm{2}}−\frac{\mathrm{3}{x}}{\mathrm{2}}\:+\mathrm{2}{k}\pi\:{or}\:\frac{\mathrm{3}{x}}{\mathrm{2}}\:=−\frac{\pi}{\mathrm{2}}\:+\frac{\mathrm{3}{x}}{\mathrm{2}}\:+\mathrm{2}{k}\pi\:\Rightarrow \\ $$$$\mathrm{3}{x}\:=\frac{\pi}{\mathrm{2}}\:+\mathrm{2}{k}\pi\:{or}\:\mathrm{2}{k}\pi=\frac{\pi}{\mathrm{2}}\left(\rightarrow{impossible}\right)\:\Rightarrow{x}=\frac{\pi}{\mathrm{6}}\:+\frac{\mathrm{2}{k}\pi}{\mathrm{3}} \\ $$$${k}\:\in{Z}\:\:{if}\:{we}\:{consider}\:\:{sinx}\:+{sin}\left(\mathrm{2}{x}\right)+{sin}\left(\mathrm{3}{x}\right)={cosx}\:+{cos}\left(\mathrm{2}{x}\right) \\ $$$$+{cos}\left(\mathrm{3}{x}\right)\:{we}\:{solve}\:{u}_{\mathrm{3}} ={v}_{\mathrm{3}} −\mathrm{1}\:{but}\:{you}\:{find}\:{a}\:{lots}\:{of}\:{calculus}… \\ $$$$ \\ $$
Commented by aliesam last updated on 18/Jul/19
god bless you sir
$${god}\:{bless}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 18/Jul/19
we have cosp +cosq =2cos(((p+q)/2))cos(((p−q)/2)) ⇒ cosx +cos(2x)+cos(3x) =cosx +cos(3x) +cos(2x) =2cos(2x)cosx +cos(2x) =cos(2x){2cosx +1} also sinx +sin(2x)+sin(3x) =cos((π/2)−x)+cos((π/2)−3x)+sin(2x) =2 cos(((π−4x)/2))cos(x) +sin(2x)=2sin(2x)cosx +sin(2x) =sin(2x){2cosx+1} (e) ⇒cos(2x)(2cosx+1)=sin(2x)(2cosx +1) ⇒ (2cosx +1)(cos(2x)−sin(2x))=0 ⇒2cosx +1=0 or cos(2x)−sin(2x)=0 2ccosx +1=0 ⇔cosx =−(1/2) =cos(((2π)/3)) ⇒x=((2π)/3) +2kπ or x =−((2π)/3) +2kπ (k∈Z) cos(2x)−sin(2x)=0 ⇔cos(2x)=sin(2x) ⇔cos(2x)=cos((π/2)−2x) ⇔2x =(π/2) −2x +2kπ or 2x =−(π/2)+2x +2kπ ⇔ 4x =(π/2) +2kπ or 2kπ =(π/2)( impossible) ⇒x=(π/8) +((kπ)/2) S ={((2π)/3) +2kπ}∪{−((2π)/3)+2kπ}∪{(π/8) +((kπ)/2)} k from Z.
$${we}\:{have}\:{cosp}\:+{cosq}\:=\mathrm{2}{cos}\left(\frac{{p}+{q}}{\mathrm{2}}\right){cos}\left(\frac{{p}−{q}}{\mathrm{2}}\right)\:\Rightarrow \\ $$$${cosx}\:+{cos}\left(\mathrm{2}{x}\right)+{cos}\left(\mathrm{3}{x}\right)\:={cosx}\:+{cos}\left(\mathrm{3}{x}\right)\:+{cos}\left(\mathrm{2}{x}\right) \\ $$$$=\mathrm{2}{cos}\left(\mathrm{2}{x}\right){cosx}\:+{cos}\left(\mathrm{2}{x}\right)\:={cos}\left(\mathrm{2}{x}\right)\left\{\mathrm{2}{cosx}\:+\mathrm{1}\right\}\:{also} \\ $$$${sinx}\:+{sin}\left(\mathrm{2}{x}\right)+{sin}\left(\mathrm{3}{x}\right)\:={cos}\left(\frac{\pi}{\mathrm{2}}−{x}\right)+{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{3}{x}\right)+{sin}\left(\mathrm{2}{x}\right) \\ $$$$=\mathrm{2}\:{cos}\left(\frac{\pi−\mathrm{4}{x}}{\mathrm{2}}\right){cos}\left({x}\right)\:+{sin}\left(\mathrm{2}{x}\right)=\mathrm{2}{sin}\left(\mathrm{2}{x}\right){cosx}\:+{sin}\left(\mathrm{2}{x}\right) \\ $$$$={sin}\left(\mathrm{2}{x}\right)\left\{\mathrm{2}{cosx}+\mathrm{1}\right\} \\ $$$$\left({e}\right)\:\Rightarrow{cos}\left(\mathrm{2}{x}\right)\left(\mathrm{2}{cosx}+\mathrm{1}\right)={sin}\left(\mathrm{2}{x}\right)\left(\mathrm{2}{cosx}\:+\mathrm{1}\right)\:\Rightarrow \\ $$$$\left(\mathrm{2}{cosx}\:+\mathrm{1}\right)\left({cos}\left(\mathrm{2}{x}\right)−{sin}\left(\mathrm{2}{x}\right)\right)=\mathrm{0}\:\Rightarrow\mathrm{2}{cosx}\:+\mathrm{1}=\mathrm{0}\:{or} \\ $$$${cos}\left(\mathrm{2}{x}\right)−{sin}\left(\mathrm{2}{x}\right)=\mathrm{0}\: \\ $$$$\mathrm{2}{ccosx}\:+\mathrm{1}=\mathrm{0}\:\Leftrightarrow{cosx}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:={cos}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\:\Rightarrow{x}=\frac{\mathrm{2}\pi}{\mathrm{3}}\:+\mathrm{2}{k}\pi\:{or} \\ $$$${x}\:=−\frac{\mathrm{2}\pi}{\mathrm{3}}\:+\mathrm{2}{k}\pi\:\:\left({k}\in{Z}\right) \\ $$$${cos}\left(\mathrm{2}{x}\right)−{sin}\left(\mathrm{2}{x}\right)=\mathrm{0}\:\Leftrightarrow{cos}\left(\mathrm{2}{x}\right)={sin}\left(\mathrm{2}{x}\right)\:\Leftrightarrow{cos}\left(\mathrm{2}{x}\right)={cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{2}{x}\right) \\ $$$$\Leftrightarrow\mathrm{2}{x}\:=\frac{\pi}{\mathrm{2}}\:−\mathrm{2}{x}\:+\mathrm{2}{k}\pi\:{or}\:\mathrm{2}{x}\:=−\frac{\pi}{\mathrm{2}}+\mathrm{2}{x}\:+\mathrm{2}{k}\pi\:\Leftrightarrow \\ $$$$\mathrm{4}{x}\:=\frac{\pi}{\mathrm{2}}\:+\mathrm{2}{k}\pi\:\:{or}\:\mathrm{2}{k}\pi\:=\frac{\pi}{\mathrm{2}}\left(\:{impossible}\right)\:\Rightarrow{x}=\frac{\pi}{\mathrm{8}}\:+\frac{{k}\pi}{\mathrm{2}} \\ $$$${S}\:=\left\{\frac{\mathrm{2}\pi}{\mathrm{3}}\:+\mathrm{2}{k}\pi\right\}\cup\left\{−\frac{\mathrm{2}\pi}{\mathrm{3}}+\mathrm{2}{k}\pi\right\}\cup\left\{\frac{\pi}{\mathrm{8}}\:+\frac{{k}\pi}{\mathrm{2}}\right\}\:{k}\:{from}\:{Z}. \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 18/Jul/19
you are welcome sir your equation is solved next...
$${you}\:{are}\:{welcome}\:{sir}\:{your}\:{equation}\:{is}\:{solved}\:{next}… \\ $$
Commented by aliesam last updated on 18/Jul/19
great work sir
$${great}\:{work}\:{sir}\: \\ $$$$ \\ $$
Commented by aliesam last updated on 18/Jul/19
Answered by Chi Mes Try last updated on 18/Jul/19
I will try sinx + 2sinxcosx + sin2xcosx + cos2xsinx = cosx sinx + 2sinxcosx + 2sinxcos^2 x + sinxcos^2 x − sin^3 x = cosx sinx + 2sinxcosx + 2sinxcos^2 x + sinxcos^2 x − sinx + sinxcos^2 x = cosx 4sinxcos^2 x + 2sinxcosx = cosx (4sinx)cos^2 x + (2sinx−1)cosx + 0 = 0 by quadratic formular in term of cosx cosx = ((1−2sinx ± (√((2sinx−1)^2 −4(4sinx)(0))))/(2(4sinx))) cosx = (((1−2sinx) ± (2sinx−1))/(8sinx)) cosx = (((1−2sinx) + (2sinx−1))/(8sinx)) cosx = (0/(8sinx)) cosx = 0 hence.... x = 90° by...Chimestry
$$ \\ $$$$ \\ $$$${I}\:{will}\:{try} \\ $$$$ \\ $$$${sinx}\:+\:\mathrm{2}{sinxcosx}\:+\:{sin}\mathrm{2}{xcosx}\:+\:{cos}\mathrm{2}{xsinx}\:=\:{cosx} \\ $$$${sinx}\:+\:\mathrm{2}{sinxcosx}\:+\:\mathrm{2}{sinxcos}^{\mathrm{2}} {x}\:+\:{sinxcos}^{\mathrm{2}} {x}\:−\:{sin}^{\mathrm{3}} {x}\:=\:{cosx} \\ $$$${sinx}\:+\:\mathrm{2}{sinxcosx}\:+\:\mathrm{2}{sinxcos}^{\mathrm{2}} {x}\:+\:{sinxcos}^{\mathrm{2}} {x}\:−\:{sinx}\:+\:{sinxcos}^{\mathrm{2}} {x}\:=\:{cosx} \\ $$$$\mathrm{4}{sinxcos}^{\mathrm{2}} {x}\:+\:\mathrm{2}{sinxcosx}\:=\:{cosx} \\ $$$$\left(\mathrm{4}{sinx}\right){cos}^{\mathrm{2}} {x}\:+\:\left(\mathrm{2}{sinx}−\mathrm{1}\right){cosx}\:+\:\mathrm{0}\:=\:\mathrm{0} \\ $$$${by}\:{quadratic}\:{formular}\:{in}\:{term}\:{of}\:{cosx} \\ $$$${cosx}\:=\:\frac{\mathrm{1}−\mathrm{2}{sinx}\:\pm\:\sqrt{\left(\mathrm{2}{sinx}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{4}{sinx}\right)\left(\mathrm{0}\right)}}{\mathrm{2}\left(\mathrm{4}{sinx}\right)} \\ $$$${cosx}\:=\:\frac{\left(\mathrm{1}−\mathrm{2}{sinx}\right)\:\pm\:\left(\mathrm{2}{sinx}−\mathrm{1}\right)}{\mathrm{8}{sinx}} \\ $$$${cosx}\:=\:\frac{\left(\mathrm{1}−\mathrm{2}{sinx}\right)\:+\:\left(\mathrm{2}{sinx}−\mathrm{1}\right)}{\mathrm{8}{sinx}} \\ $$$${cosx}\:=\:\frac{\mathrm{0}}{\mathrm{8}{sinx}} \\ $$$${cosx}\:=\:\mathrm{0} \\ $$$${hence}….\:{x}\:=\:\mathrm{90}° \\ $$$$ \\ $$$${by}…{Chimestry} \\ $$
Commented by aliesam last updated on 18/Jul/19
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Commented by mr W last updated on 18/Jul/19
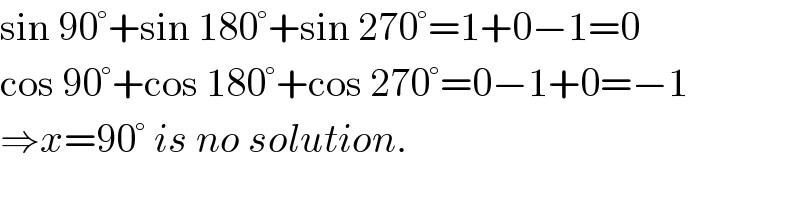
sin 90°+sin 180°+sin 270°=1+0−1=0 cos 90°+cos 180°+cos 270°=0−1+0=−1 ⇒x=90° is no solution.
$$\mathrm{sin}\:\mathrm{90}°+\mathrm{sin}\:\mathrm{180}°+\mathrm{sin}\:\mathrm{270}°=\mathrm{1}+\mathrm{0}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{cos}\:\mathrm{90}°+\mathrm{cos}\:\mathrm{180}°+\mathrm{cos}\:\mathrm{270}°=\mathrm{0}−\mathrm{1}+\mathrm{0}=−\mathrm{1} \\ $$$$\Rightarrow{x}=\mathrm{90}°\:{is}\:{no}\:{solution}. \\ $$
Answered by MJS last updated on 18/Jul/19
sin x +sin 2x +sin 3x =cos x +cos 2x +cos 3x x=2arctan t ((2t)/(t^2 +1))−((4t(t−1)(t+1))/((t^2 +1)^2 ))+((2t(t^2 −3)(3t^2 −1))/((t^2 +1)^3 ))= =−(((t−1)(t+1))/(t^2 +1))+(((t^2 −2t−1)(t^2 +2t−1))/((t^2 +1)))−(((t−1)(t+1)(t^2 −4t+1)(t^2 +4t+1))/((t^2 +1)^3 )) (((t^2 −3)(t^4 +4t^3 −6t^2 −4t+1))/((t^2 +1)^3 ))=0 t^2 −3=0 ⇒ t_(1, 2) =±(√3) t^4 +4t^3 −6t^2 −4t+1=0 t=u−1 u^4 −12u^2 +16u−4=0 (u^2 −αu−β)(u^2 +αu−γ)=0 u^4 −(α^2 +β−γ)u^2 −α(β−γ)u+βγ=0 α^2 +β−γ=12 −α(β−γ)=16 βγ=−4 ⇒ α=2(√2) β=2−2(√2) γ=2+2(√2) (u^2 −2(√2)u−2+2(√2))(u^2 +2(√2)u−2−2(√2))=0 ⇒ u_1 =(√2)−(√(4−2(√2))) ⇒ t_3 =−1+(√2)−(√(4−2(√2))) u_2 =(√2)+(√(4−2(√2))) ⇒ −1+(√2)+(√(4−2(√2))) u_3 =−(√2)−(√(4+2(√2))) ⇒ −1−(√2)−(√(4+2(√2))) u_4 =−(√2)+(√(4+2(√2))) ⇒ −1−(√2)+(√(4+2(√2))) ⇒ x_(1, 2) =±(2/3)π x_3 =−(3/8)π x_4 =(5/8)π x_5 =(1/8)π x_6 =−(7/8)π ⇒ x=((1/8)+(n/2))π∨x=((2/3)+2n)π∨x=((4/3)+2n)π
$$\mathrm{sin}\:{x}\:+\mathrm{sin}\:\mathrm{2}{x}\:+\mathrm{sin}\:\mathrm{3}{x}\:=\mathrm{cos}\:{x}\:+\mathrm{cos}\:\mathrm{2}{x}\:+\mathrm{cos}\:\mathrm{3}{x} \\ $$$${x}=\mathrm{2arctan}\:{t} \\ $$$$\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{4}{t}\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{t}\left({t}^{\mathrm{2}} −\mathrm{3}\right)\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }= \\ $$$$\:\:\:\:\:=−\frac{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)}{{t}^{\mathrm{2}} +\mathrm{1}}+\frac{\left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)}−\frac{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{4}{t}+\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\frac{\left({t}^{\mathrm{2}} −\mathrm{3}\right)\left({t}^{\mathrm{4}} +\mathrm{4}{t}^{\mathrm{3}} −\mathrm{6}{t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }=\mathrm{0} \\ $$$${t}^{\mathrm{2}} −\mathrm{3}=\mathrm{0}\:\Rightarrow\:{t}_{\mathrm{1},\:\mathrm{2}} =\pm\sqrt{\mathrm{3}} \\ $$$${t}^{\mathrm{4}} +\mathrm{4}{t}^{\mathrm{3}} −\mathrm{6}{t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{1}=\mathrm{0} \\ $$$${t}={u}−\mathrm{1} \\ $$$${u}^{\mathrm{4}} −\mathrm{12}{u}^{\mathrm{2}} +\mathrm{16}{u}−\mathrm{4}=\mathrm{0} \\ $$$$\left({u}^{\mathrm{2}} −\alpha{u}−\beta\right)\left({u}^{\mathrm{2}} +\alpha{u}−\gamma\right)=\mathrm{0} \\ $$$${u}^{\mathrm{4}} −\left(\alpha^{\mathrm{2}} +\beta−\gamma\right){u}^{\mathrm{2}} −\alpha\left(\beta−\gamma\right){u}+\beta\gamma=\mathrm{0} \\ $$$$\alpha^{\mathrm{2}} +\beta−\gamma=\mathrm{12} \\ $$$$−\alpha\left(\beta−\gamma\right)=\mathrm{16} \\ $$$$\beta\gamma=−\mathrm{4} \\ $$$$\Rightarrow\:\alpha=\mathrm{2}\sqrt{\mathrm{2}}\:\:\beta=\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}\:\:\gamma=\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\left({u}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}{u}−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}\right)\left({u}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{2}}{u}−\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${u}_{\mathrm{1}} =\sqrt{\mathrm{2}}−\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}\:\Rightarrow\:{t}_{\mathrm{3}} =−\mathrm{1}+\sqrt{\mathrm{2}}−\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${u}_{\mathrm{2}} =\sqrt{\mathrm{2}}+\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}\:\Rightarrow\:−\mathrm{1}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${u}_{\mathrm{3}} =−\sqrt{\mathrm{2}}−\sqrt{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}}\:\Rightarrow\:−\mathrm{1}−\sqrt{\mathrm{2}}−\sqrt{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${u}_{\mathrm{4}} =−\sqrt{\mathrm{2}}+\sqrt{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}}\:\Rightarrow\:−\mathrm{1}−\sqrt{\mathrm{2}}+\sqrt{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow \\ $$$${x}_{\mathrm{1},\:\mathrm{2}} =\pm\frac{\mathrm{2}}{\mathrm{3}}\pi \\ $$$${x}_{\mathrm{3}} =−\frac{\mathrm{3}}{\mathrm{8}}\pi \\ $$$${x}_{\mathrm{4}} =\frac{\mathrm{5}}{\mathrm{8}}\pi \\ $$$${x}_{\mathrm{5}} =\frac{\mathrm{1}}{\mathrm{8}}\pi \\ $$$${x}_{\mathrm{6}} =−\frac{\mathrm{7}}{\mathrm{8}}\pi \\ $$$$\Rightarrow\:{x}=\left(\frac{\mathrm{1}}{\mathrm{8}}+\frac{{n}}{\mathrm{2}}\right)\pi\vee{x}=\left(\frac{\mathrm{2}}{\mathrm{3}}+\mathrm{2}{n}\right)\pi\vee{x}=\left(\frac{\mathrm{4}}{\mathrm{3}}+\mathrm{2}{n}\right)\pi \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *