Question Number 50892 by peter frank last updated on 21/Dec/18
![solve the equation tan 3θcotθ+1=0 for 0≤θ≤180 b)show that if cos 2θ is not zero then cos 2θ+sec 2θ=2[((cos^4 θ+sin^4 θ)/(cos^4 θ−sin^4 θ))] c)find the limit of ((tan (θ/3))/(3θ)) as θ→0](https://www.tinkutara.com/question/Q50892.png)
$${solve}\:{the}\:{equation} \\ $$$$\mathrm{tan}\:\mathrm{3}\theta{cot}\theta+\mathrm{1}=\mathrm{0}\:{for} \\ $$$$\mathrm{0}\leqslant\theta\leqslant\mathrm{180} \\ $$$$\left.{b}\right){show}\:{that}\:{if}\:\mathrm{cos}\:\mathrm{2}\theta\:{is}\:{not}\:{zero} \\ $$$${then} \\ $$$$\mathrm{cos}\:\mathrm{2}\theta+\mathrm{sec}\:\mathrm{2}\theta=\mathrm{2}\left[\frac{\mathrm{cos}\:^{\mathrm{4}} \theta+\mathrm{sin}\:^{\mathrm{4}} \theta}{\mathrm{cos}\:^{\mathrm{4}} \theta−\mathrm{sin}\:^{\mathrm{4}} \theta}\right] \\ $$$$\left.{c}\right){find}\:{the}\:{limit}\:{of} \\ $$$$\frac{\mathrm{tan}\:\frac{\theta}{\mathrm{3}}}{\mathrm{3}\theta}\:{as}\:\theta\rightarrow\mathrm{0} \\ $$$$ \\ $$
Answered by kaivan.ahmadi last updated on 21/Dec/18
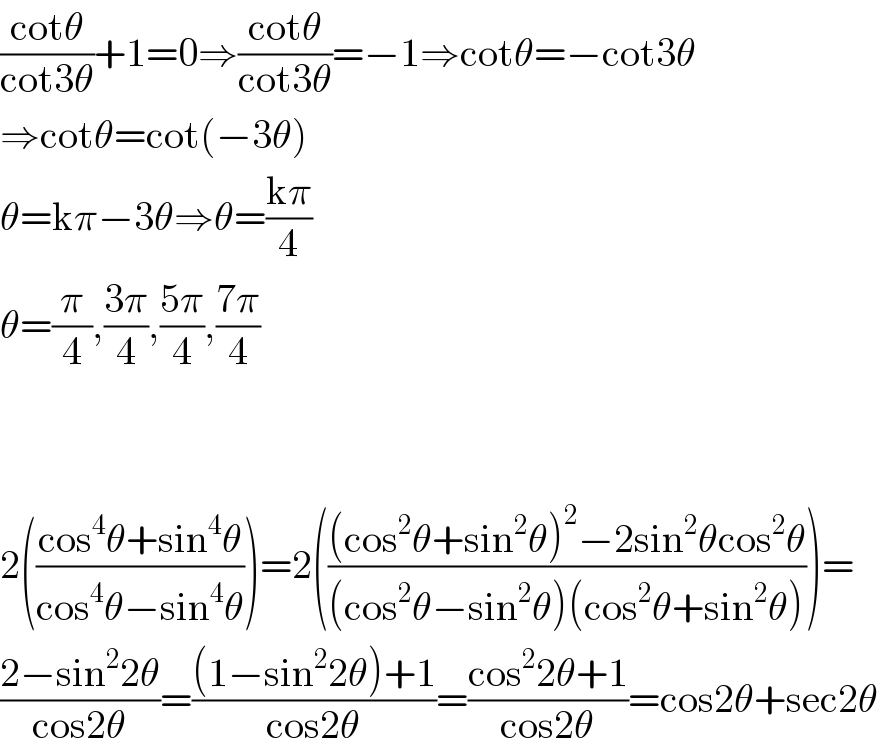
$$\frac{\mathrm{cot}\theta}{\mathrm{cot3}\theta}+\mathrm{1}=\mathrm{0}\Rightarrow\frac{\mathrm{cot}\theta}{\mathrm{cot3}\theta}=−\mathrm{1}\Rightarrow\mathrm{cot}\theta=−\mathrm{cot3}\theta \\ $$$$\Rightarrow\mathrm{cot}\theta=\mathrm{cot}\left(−\mathrm{3}\theta\right) \\ $$$$\theta=\mathrm{k}\pi−\mathrm{3}\theta\Rightarrow\theta=\frac{\mathrm{k}\pi}{\mathrm{4}} \\ $$$$\theta=\frac{\pi}{\mathrm{4}},\frac{\mathrm{3}\pi}{\mathrm{4}},\frac{\mathrm{5}\pi}{\mathrm{4}},\frac{\mathrm{7}\pi}{\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{2}\left(\frac{\mathrm{cos}^{\mathrm{4}} \theta+\mathrm{sin}^{\mathrm{4}} \theta}{\mathrm{cos}^{\mathrm{4}} \theta−\mathrm{sin}^{\mathrm{4}} \theta}\right)=\mathrm{2}\left(\frac{\left(\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{sin}^{\mathrm{2}} \theta\right)^{\mathrm{2}} −\mathrm{2sin}^{\mathrm{2}} \theta\mathrm{cos}^{\mathrm{2}} \theta}{\left(\mathrm{cos}^{\mathrm{2}} \theta−\mathrm{sin}^{\mathrm{2}} \theta\right)\left(\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{sin}^{\mathrm{2}} \theta\right)}\right)= \\ $$$$\frac{\mathrm{2}−\mathrm{sin}^{\mathrm{2}} \mathrm{2}\theta}{\mathrm{cos2}\theta}=\frac{\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{2}\theta\right)+\mathrm{1}}{\mathrm{cos2}\theta}=\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{2}\theta+\mathrm{1}}{\mathrm{cos2}\theta}=\mathrm{cos2}\theta+\mathrm{sec2}\theta \\ $$
Answered by peter frank last updated on 21/Dec/18
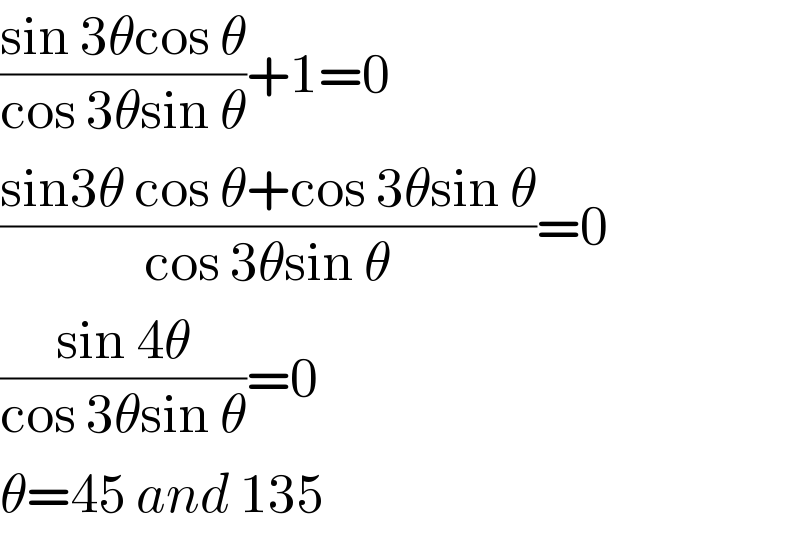
$$\frac{\mathrm{sin}\:\mathrm{3}\theta\mathrm{cos}\:\theta}{\mathrm{cos}\:\mathrm{3}\theta\mathrm{sin}\:\theta}+\mathrm{1}=\mathrm{0} \\ $$$$\frac{\mathrm{sin3}\theta\:\mathrm{cos}\:\theta+\mathrm{cos}\:\mathrm{3}\theta\mathrm{sin}\:\theta}{\mathrm{cos}\:\mathrm{3}\theta\mathrm{sin}\:\theta}=\mathrm{0} \\ $$$$\frac{\mathrm{sin}\:\mathrm{4}\theta}{\mathrm{cos}\:\mathrm{3}\theta\mathrm{sin}\:\theta}=\mathrm{0} \\ $$$$\theta=\mathrm{45}\:{and}\:\mathrm{135} \\ $$
Answered by peter frank last updated on 21/Dec/18
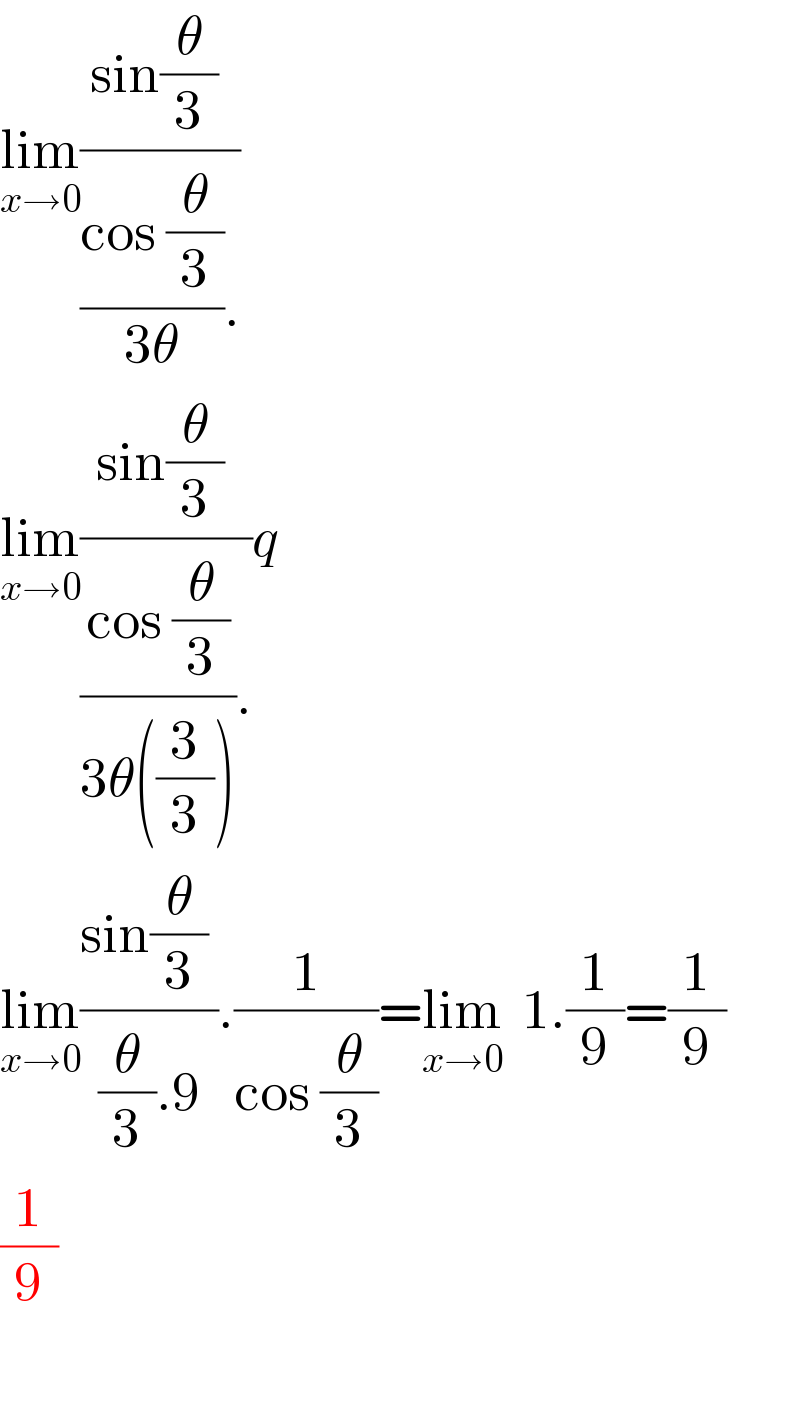
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\frac{\theta}{\mathrm{3}}\:}{\frac{\mathrm{cos}\:\frac{\theta}{\mathrm{3}}}{\mathrm{3}\theta}.} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\frac{\theta}{\mathrm{3}}\:}{\frac{\mathrm{cos}\:\frac{\theta}{\mathrm{3}}}{\mathrm{3}\theta\left(\frac{\mathrm{3}}{\mathrm{3}}\right)}.}{q} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\frac{\theta}{\mathrm{3}}\:}{\frac{\theta}{\mathrm{3}}.\mathrm{9}}.\frac{\mathrm{1}}{\mathrm{cos}\:\frac{\theta}{\mathrm{3}}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\mathrm{1}.\frac{\mathrm{1}}{\mathrm{9}}=\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$ \\ $$
