Question Number 166539 by daus last updated on 22/Feb/22
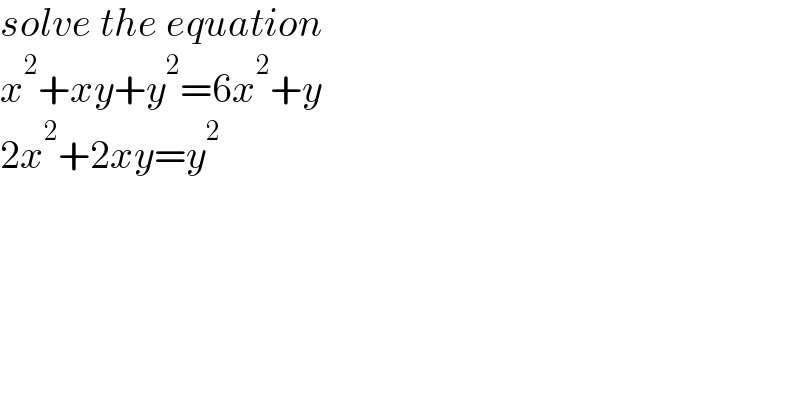
$${solve}\:{the}\:{equation} \\ $$$${x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} =\mathrm{6}{x}^{\mathrm{2}} +{y}\: \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{xy}={y}^{\mathrm{2}} \\ $$
Commented by cortano1 last updated on 22/Feb/22
![{ ((xy+y^2 =5x^2 +y)),((2x^2 +2xy=y^2 )) :}⇒(1)+(2) 3xy+2x^2 =5x^2 +y ⇒3x^2 −3xy+y = 0 ⇒3x^2 = y(3x−1) ⇒y=((3x^2 )/(3x−1)) ⇒2x(x+y)=y^2 ⇒2x(x+((3x^2 )/(3x−1)))= ((9x^4 )/((3x−1)^2 )) ⇒2x(((6x^2 −x)/(3x−1)))=((9x^4 )/((3x−1)^2 )) ⇒2x^2 (3x−1)(6x−1)−9x^4 =0 ⇒x^2 [ 2(18x^2 −9x+1)−9]=0 { ((x=0 , y=0)),((36x^2 −18x−7=0⇒ { ((x_1 =((3+(√(37)))/(12)))),((x_2 =((3−(√(37)))/(12)))) :})) :}](https://www.tinkutara.com/question/Q166566.png)
$$\begin{cases}{\mathrm{xy}+\mathrm{y}^{\mathrm{2}} =\mathrm{5x}^{\mathrm{2}} +\mathrm{y}}\\{\mathrm{2x}^{\mathrm{2}} +\mathrm{2xy}=\mathrm{y}^{\mathrm{2}} }\end{cases}\Rightarrow\left(\mathrm{1}\right)+\left(\mathrm{2}\right) \\ $$$$\:\mathrm{3xy}+\mathrm{2x}^{\mathrm{2}} =\mathrm{5x}^{\mathrm{2}} +\mathrm{y}\: \\ $$$$\:\Rightarrow\mathrm{3x}^{\mathrm{2}} −\mathrm{3xy}+\mathrm{y}\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{3x}^{\mathrm{2}} \:=\:\mathrm{y}\left(\mathrm{3x}−\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{3x}−\mathrm{1}}\: \\ $$$$\Rightarrow\mathrm{2x}\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{y}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2x}\left(\mathrm{x}+\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{3x}−\mathrm{1}}\right)=\:\frac{\mathrm{9x}^{\mathrm{4}} }{\left(\mathrm{3x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{2x}\left(\frac{\mathrm{6x}^{\mathrm{2}} −\mathrm{x}}{\mathrm{3x}−\mathrm{1}}\right)=\frac{\mathrm{9x}^{\mathrm{4}} }{\left(\mathrm{3x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{2x}^{\mathrm{2}} \left(\mathrm{3x}−\mathrm{1}\right)\left(\mathrm{6x}−\mathrm{1}\right)−\mathrm{9x}^{\mathrm{4}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} \:\left[\:\mathrm{2}\left(\mathrm{18x}^{\mathrm{2}} −\mathrm{9x}+\mathrm{1}\right)−\mathrm{9}\right]=\mathrm{0} \\ $$$$\:\begin{cases}{\mathrm{x}=\mathrm{0}\:,\:\mathrm{y}=\mathrm{0}}\\{\mathrm{36x}^{\mathrm{2}} −\mathrm{18x}−\mathrm{7}=\mathrm{0}\Rightarrow\begin{cases}{\mathrm{x}_{\mathrm{1}} =\frac{\mathrm{3}+\sqrt{\mathrm{37}}}{\mathrm{12}}}\\{\mathrm{x}_{\mathrm{2}} =\frac{\mathrm{3}−\sqrt{\mathrm{37}}}{\mathrm{12}}}\end{cases}}\end{cases} \\ $$
Commented by daus last updated on 23/Feb/22

$${thank}\:{you} \\ $$
