Question Number 129388 by MathSh last updated on 15/Jan/21
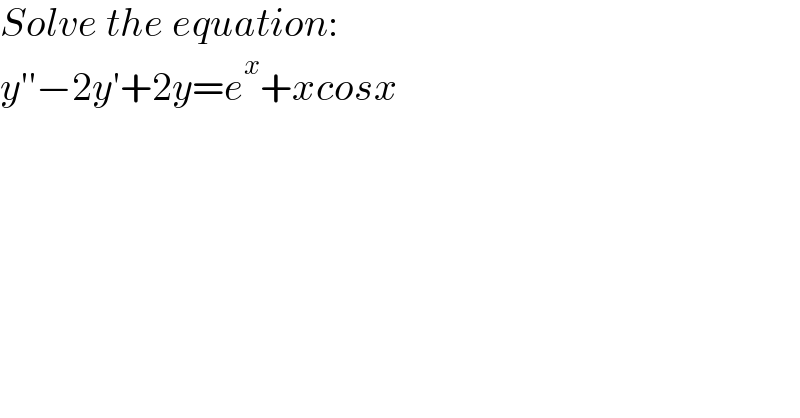
$${Solve}\:{the}\:{equation}: \\ $$$${y}''−\mathrm{2}{y}'+\mathrm{2}{y}={e}^{{x}} +{xcosx} \\ $$
Answered by mathmax by abdo last updated on 16/Jan/21
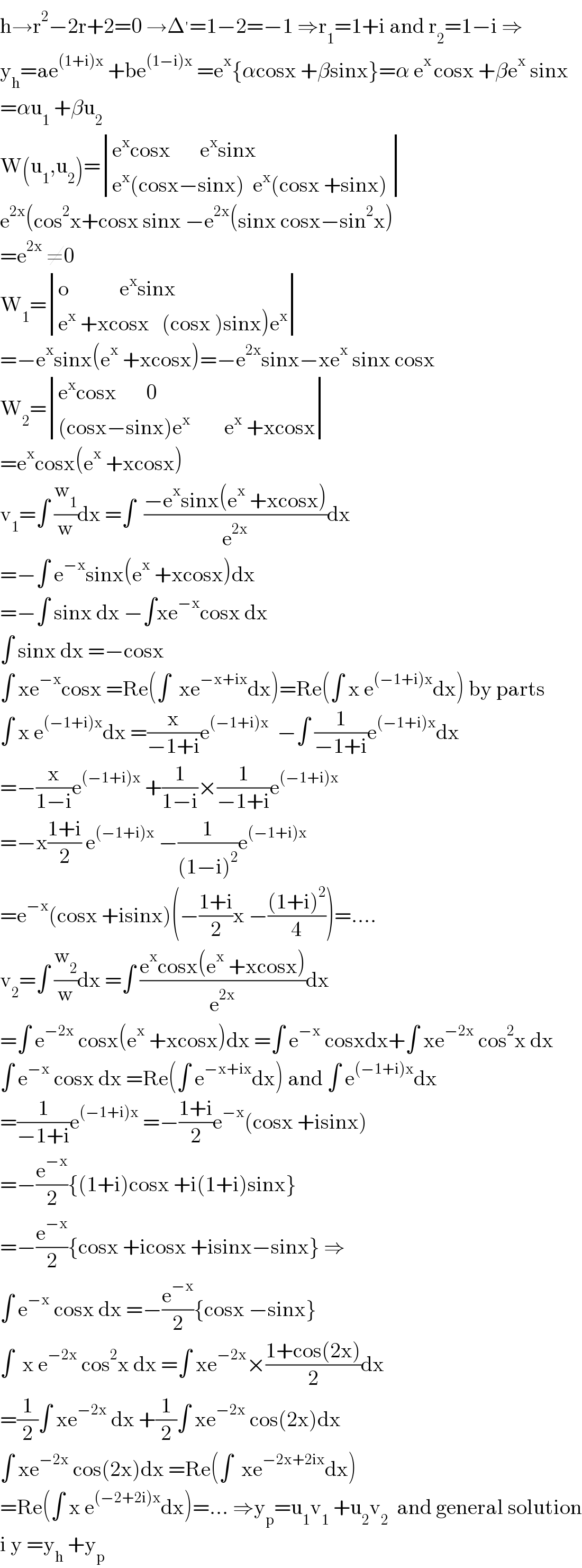
$$\mathrm{h}\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{2r}+\mathrm{2}=\mathrm{0}\:\rightarrow\Delta^{'} =\mathrm{1}−\mathrm{2}=−\mathrm{1}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\mathrm{1}+\mathrm{i}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\mathrm{1}−\mathrm{i}\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{h}} =\mathrm{ae}^{\left(\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \:+\mathrm{be}^{\left(\mathrm{1}−\mathrm{i}\right)\mathrm{x}} \:=\mathrm{e}^{\mathrm{x}} \left\{\alpha\mathrm{cosx}\:+\beta\mathrm{sinx}\right\}=\alpha\:\mathrm{e}^{\mathrm{x}\:} \mathrm{cosx}\:+\beta\mathrm{e}^{\mathrm{x}} \:\mathrm{sinx} \\ $$$$=\alpha\mathrm{u}_{\mathrm{1}} \:+\beta\mathrm{u}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)=\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \mathrm{cosx}\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} \mathrm{sinx}}\\{\mathrm{e}^{\mathrm{x}} \left(\mathrm{cosx}−\mathrm{sinx}\right)\:\:\mathrm{e}^{\mathrm{x}} \left(\mathrm{cosx}\:+\mathrm{sinx}\right)\:}\end{vmatrix} \\ $$$$\mathrm{e}^{\mathrm{2x}} \left(\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{cosx}\:\mathrm{sinx}\:−\mathrm{e}^{\mathrm{2x}} \left(\mathrm{sinx}\:\mathrm{cosx}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)\right. \\ $$$$=\mathrm{e}^{\mathrm{2x}} \:\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} \mathrm{sinx}}\\{\left.\mathrm{e}^{\mathrm{x}} \:+\mathrm{xcosx}\:\:\:\left(\mathrm{cosx}\:\right)\mathrm{sinx}\right)\mathrm{e}^{\mathrm{x}} }\end{vmatrix} \\ $$$$=−\mathrm{e}^{\mathrm{x}} \mathrm{sinx}\left(\mathrm{e}^{\mathrm{x}} \:+\mathrm{xcosx}\right)=−\mathrm{e}^{\mathrm{2x}} \mathrm{sinx}−\mathrm{xe}^{\mathrm{x}} \:\mathrm{sinx}\:\mathrm{cosx} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \mathrm{cosx}\:\:\:\:\:\:\:\mathrm{0}}\\{\left(\mathrm{cosx}−\mathrm{sinx}\right)\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} \:+\mathrm{xcosx}}\end{vmatrix} \\ $$$$=\mathrm{e}^{\mathrm{x}} \mathrm{cosx}\left(\mathrm{e}^{\mathrm{x}} \:+\mathrm{xcosx}\right) \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\:\frac{−\mathrm{e}^{\mathrm{x}} \mathrm{sinx}\left(\mathrm{e}^{\mathrm{x}} \:+\mathrm{xcosx}\right)}{\mathrm{e}^{\mathrm{2x}} }\mathrm{dx} \\ $$$$=−\int\:\mathrm{e}^{−\mathrm{x}} \mathrm{sinx}\left(\mathrm{e}^{\mathrm{x}} \:+\mathrm{xcosx}\right)\mathrm{dx} \\ $$$$=−\int\:\mathrm{sinx}\:\mathrm{dx}\:−\int\mathrm{xe}^{−\mathrm{x}} \mathrm{cosx}\:\mathrm{dx} \\ $$$$\int\:\mathrm{sinx}\:\mathrm{dx}\:=−\mathrm{cosx} \\ $$$$\int\:\mathrm{xe}^{−\mathrm{x}} \mathrm{cosx}\:=\mathrm{Re}\left(\int\:\:\mathrm{xe}^{−\mathrm{x}+\mathrm{ix}} \mathrm{dx}\right)=\mathrm{Re}\left(\int\:\mathrm{x}\:\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \mathrm{dx}\right)\:\mathrm{by}\:\mathrm{parts} \\ $$$$\int\:\mathrm{x}\:\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \mathrm{dx}\:=\frac{\mathrm{x}}{−\mathrm{1}+\mathrm{i}}\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \:\:−\int\:\frac{\mathrm{1}}{−\mathrm{1}+\mathrm{i}}\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \mathrm{dx} \\ $$$$=−\frac{\mathrm{x}}{\mathrm{1}−\mathrm{i}}\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \:+\frac{\mathrm{1}}{\mathrm{1}−\mathrm{i}}×\frac{\mathrm{1}}{−\mathrm{1}+\mathrm{i}}\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \\ $$$$=−\mathrm{x}\frac{\mathrm{1}+\mathrm{i}}{\mathrm{2}}\:\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \:−\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{i}\right)^{\mathrm{2}} }\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \\ $$$$=\mathrm{e}^{−\mathrm{x}} \left(\mathrm{cosx}\:+\mathrm{isinx}\right)\left(−\frac{\mathrm{1}+\mathrm{i}}{\mathrm{2}}\mathrm{x}\:−\frac{\left(\mathrm{1}+\mathrm{i}\right)^{\mathrm{2}} }{\mathrm{4}}\right)=…. \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\frac{\mathrm{e}^{\mathrm{x}} \mathrm{cosx}\left(\mathrm{e}^{\mathrm{x}} \:+\mathrm{xcosx}\right)}{\mathrm{e}^{\mathrm{2x}} }\mathrm{dx} \\ $$$$=\int\:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{cosx}\left(\mathrm{e}^{\mathrm{x}} \:+\mathrm{xcosx}\right)\mathrm{dx}\:=\int\:\mathrm{e}^{−\mathrm{x}} \:\mathrm{cosxdx}+\int\:\mathrm{xe}^{−\mathrm{2x}} \:\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx} \\ $$$$\int\:\mathrm{e}^{−\mathrm{x}} \:\mathrm{cosx}\:\mathrm{dx}\:=\mathrm{Re}\left(\int\:\mathrm{e}^{−\mathrm{x}+\mathrm{ix}} \mathrm{dx}\right)\:\mathrm{and}\:\int\:\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{−\mathrm{1}+\mathrm{i}}\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \:=−\frac{\mathrm{1}+\mathrm{i}}{\mathrm{2}}\mathrm{e}^{−\mathrm{x}} \left(\mathrm{cosx}\:+\mathrm{isinx}\right) \\ $$$$=−\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\left\{\left(\mathrm{1}+\mathrm{i}\right)\mathrm{cosx}\:+\mathrm{i}\left(\mathrm{1}+\mathrm{i}\right)\mathrm{sinx}\right\} \\ $$$$=−\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\left\{\mathrm{cosx}\:+\mathrm{icosx}\:+\mathrm{isinx}−\mathrm{sinx}\right\}\:\Rightarrow \\ $$$$\int\:\mathrm{e}^{−\mathrm{x}} \:\mathrm{cosx}\:\mathrm{dx}\:=−\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\left\{\mathrm{cosx}\:−\mathrm{sinx}\right\} \\ $$$$\int\:\:\mathrm{x}\:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}\:=\int\:\mathrm{xe}^{−\mathrm{2x}} ×\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{xe}^{−\mathrm{2x}} \:\mathrm{dx}\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{xe}^{−\mathrm{2x}} \:\mathrm{cos}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$$$\int\:\mathrm{xe}^{−\mathrm{2x}} \:\mathrm{cos}\left(\mathrm{2x}\right)\mathrm{dx}\:=\mathrm{Re}\left(\int\:\:\mathrm{xe}^{−\mathrm{2x}+\mathrm{2ix}} \mathrm{dx}\right) \\ $$$$=\mathrm{Re}\left(\int\:\mathrm{x}\:\mathrm{e}^{\left(−\mathrm{2}+\mathrm{2i}\right)\mathrm{x}} \mathrm{dx}\right)=…\:\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \:\:\mathrm{and}\:\mathrm{general}\:\mathrm{solution} \\ $$$$\mathrm{i}\:\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$
Commented by SANOGO last updated on 30/Aug/21

